Разрез на сети

5. Разрез на сети

Представим некоторую сеть. Разобьем множество вершин сети на два непересекающихся подмножества A и B так, чтобы исток I попал в подмножество A, а сток S попал в подмножество B. В результате такого разбиения появляются ребра (i, j), конечные точки которых оказываются в разных подмножествах.

Совокупность ребер (i, j), начальные точки которых принадлежат подмножеству A, а конечные точки – подмножеству B, называют разрезом сети и обозначают A/B.

На рис. 1.9 изображена некоторая сеть. Стрелки указывают положительное направление потока. На сети произведено два разреза: I и II. При разрезе I образовалось два подмножества вершин сети: подмножество A = {1, 2} и B = {3, 4, 5}, а ребрами, образующим разрез, стали (1, 3), (1, 4), (2, 4). При разрезе II образовались подмножества A = {1, 2, 3, 4} и B = {5} с образующими разрез ребрами (3, 5) и (4, 5).

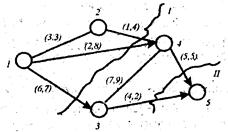
Рис. 1.9

Величина , представляющая сумму пропускных способностей всех ребер разреза, называется пропускной способностью разреза.

Если на сети задан поток X = {xB_ijB} и разрез (A/B), то величина , представляющая сумму потоков по всем ребрам разреза, называется потоком через разрез.

Для разреза I R(I) = rB_13B + rB_{14 B}+ rB_24B = 6 + 2 + 1 = 9. X(I) = xB_13B + xB_14B + xB_24B = 4 + 2 + 0 = 6. Для разреза II – R(II) = 9, X(II) = 6.

В общем случае, если на сети задан поток X = {xij} и произведен разрез (A/B), то хотя бы одно ребро любого полного пути, идущего из истока в сток, будет обязательно принадлежать разрезу (A/B). Напомним, что величина потока по любому полному пути не превышает пропускную способность каждого его ребра, а потому величина X суммарного потока, стремящегося из истока в сток, не может повысить пропускную способность любого разреза сети, т.е.

 (1.5)

В теории потоков утверждается, что если удастся построить на сети поток XP^{* P}= {xB_ijPB^*P}, величина которого равна пропускной способности некоторого разреза (A/B), то этот поток будет максимальным, а разрез обладать минимальной пропускной способностью. Ниже приводится теорема о максимальном потоке, имеющая большое прикладное значение.

Теорема Форда - Фалкерсона. На любой сети сети максимльная величина потока из истока I в исток S равна максимальной пропускной способности разреза, отделяющего I от S.

6. Алгоритм решения задачи о максимальном потоке

В разделе 4 был проведен расчет мощности потока, но ничего не было сказано о том, будет ли этот поток максимальным. Чтобы ответить на этот вопрос, необходимо исследовать этот поток.

Пусть задан некоторый поток X = {xij}. Разобьем сеть таким образом, чтобы к подмножеству A отошли исток I и все те вершины i, которые достигаются из истока I хотя бы по одному пути, состоящему из ненасыщенных ребер; к подмножеству B отнесем вершины, которые нельзя достичь из истока по ненасыщенным ребрам. При таком разбиении возникают две ситуации:

1) сток ;

2) сток .

Рассмотрим случай 1. Если , то

Построенное разбиение является разрезом A/B. По условию разбиения для любой вершины существует путь из истока в i, состоящий из ненасыщенных ребер, а для любой вершины такого пути нет. Отсюда следует, что любое ребро (i,j) разреза A/B будет насыщенным (иначе j принадлежало бы A), т.е. xij = rij. Просуммируем все эти равенства по всем и всем и получим

 (1.6)

В этом равенстве слева – величина X потока через разрез, справа – пропускная способность R разреза A/B. Из равенства (1.6) по теореме Форда - Фалкерсона следует, что поток X = {xij} является максимальным.

Рассмотрим случай 2. Если то существует путь из ненасыщенных ребер, ведущий из истока в сток. По ребрам этого пути можно пропустить дополнительный поток величиной , где минимум берется по всем ребрам, входящими в этот путь. Потоки xB_ijB по всем остальным ребрам остаются без изменения. В результате мощность суммарного потока возрастет на величину и это будет новый поток X = {xB_ijPB^1P}.

При объединении двух рассмотренных случаев просматривается следующий алгоритм построения максимального потока:

1.   Построить некоторый начальный поток XP^0P = {xB_ijPB^0P}.

2.   Найти подмножество A вершин, достижимых из истока I по ненасыщенным ребрам. Если в этом процессе сток S не попадет в подмножество A, то построенный поток максимальный и задача решена. Если же сток S попал в A, то перейти к п. 3 алгоритма.

3.   Выделить путь из истока I в сток S, состоящий из ненасыщенных ребер, и увеличить поток xB_ijBпо каждому ребру этого пути на величину , где минимум берется по ребрам (i,j) упомянутого пути. Это означает, что будет построен новый поток XP^1P = {xB_ijPB^1P}. После этого надо вернуться к п. 2 данного алгоритма.

Замечание: при выполнении п. 3 алгоритма на каждом шаге по крайней мере одно из ненасыщенных раннее ребер становится насыщенным. Поскольку число ребер в сети конечно, то через конечное число шагов максимальный поток будет построен.

Разберем на примере предложенный алгоритм.

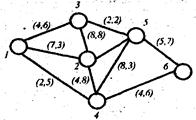
Рис. 1.10

На рис. 1.10 изображена сеть с истоком I в вершине (1) и стоком в вершине (6). В скобках проставлена пропускная способность ребер в прямом и обратном направлении. В табл. 1.2 показана матрица пропускных способностей сети.

В соответствии с п. 1 алгоритма сформируем на сети первоначальный поток XP^0P. В этом потоке по пути 1 – 3 – 5 – 6 перемещаются 2 ед., поскольку ограничивает величину потока ребро (3, 5); по пути 1 – 2 – 5 – 6 перемещается 1 ед., лимитирующим является ребро (2, 5); по пути 1 – 4 – 6 – 2 – 2 ед., и ребро (1, 4) становится насыщенным. Матрица потока представлена на табл. 1.3.

Мощность потока XP^{0 P}рассчитаем по формуле (1.4).

f = xB_12B + xB_{13 B}+ xB_14B = xB_46B + xB_56B = 1 + 2 + 2 = 2 + 3 = 5.

Таблица 1.2

i/j	1	2	3	4	5	6
1	0	7	4	2	0	0
2	3	0	8	4	1	0
3	6	8	0	0	2	0
4	5	9	0	0	8	4
5	0	5	2	3	0	5
6	0	0	0	6	7	0

Таблица 1.3

i/j	1	2	3	4	5	6
1	0	1	2	2	0	0
2	-1	0	0	0	1	0
3	-2	0	0	0	2	0
4	-2	0	9	0	4	0
5	0	-1	-2	0	0	3
6	0	0	0	-2	-3	0

Для выполнения п. 2 алгоритма рассчитаем матрицу R – XP^0P, приведенную в табл. 1.4. Элементы (r_ij – x_ij⁰) этой матрицы позволяют судить о насыщенности ребер сети. Нулевые элементы соответствуют насыщенным ребрам, ненулевые – ненасыщенным. С помощью матрицы R – XP^0P можно сформировать подмножество A вершин, в которое можно попасть из истока I, двигаясь только по ненасыщенным путям, выделить их (если поток XP^{0 P} не максимален) и с их помощью увеличить мощность потока.

Таблица 1.4

i/j	1	2	3	4	5	6
1	0	3	2	2	0	0
2	-3	0	0	2	1	0
3	-2	0	0	0	2	0
4	-2	-2	0	0	0	4
5	0	-1	-2	0	0	3
6	0	0	0	-4	-3	0

Таблица 1.5

i/j	1	2	3	4	5	6
1	0	6	2	0	0	0
2	4	0	8	4	0	0
3	8	8	0	0	0	0
4	7	9	0	0	8	2
5	0	6	4	3	0	2
6	0	0	0	8	10	0

Вершины подмножества A выделяют постепенно, начиная с истока I. Для этого просматривают первую строку матрицы R – XP^{0 P}( в общем случае строку I) и выписывают номера вершин iB_1B, iB_2B, …, iB_kB, соответствующих ненулевым элементам стоки. Это и будут вершины, в которые можно попасть из истока, перемещаясь по ненасыщенным ребрам. Запишем выявленные вершины в виде списка

Далее рассматривают каждую из вершин iB_kBполученного списка и составляют для нее свой список аналогичным образом. При этом вершины, встречающиеся в прежних списках, повторно не выписываются.

Если в этом процессе сток S не встретится, то поток максимален и задача решена; если же, напротив, при составлении очередного списка в нем появится сток S, то поток не максимален и его мощность можно увеличить. Для этого выделяют ненасыщенный путь из истока в сток. Построение ненасыщенного пути из I в S начинают с последнего ребра этого пути. Этим ребром будет (i B_n-1B, S), где i B_{n-1 B}– вершина, в список которой попал сток S. Далее находят ребро (i B_n-2B, i B_n-1B), где i B_n-2B - вершина, в список которой попала вершина i B_n-1B, и т.д., пока не встретится ребро (I, iB_1B), которым начинается искомый ненасыщенный путь.

В данном примере I = 1, S = 6. Построим подмножество A, начиная с вершины. В табл. 1.4 в первой строке ненулевые элементы стоят во втором и третьем столбцах. Следовательно, запишем .

Последовательно составляем списки вершин 2 и 3. Во второй строке матрицы три элемента отличны от нуля: 4, 8, 4. Цифры 4 и 8 соответствуют вершинам 7 и 3, которые уже вошли в подмножество A, поэтому эти вершины повторно в списки не включаем. В четвертом столбце цифра 4 встречается впервые, поэтому включаем ее в список вершины . Переходим к вершине 3. В третьей строке матрицы R – XP^{0 P}ненулевым элементам соответствуют вершины 1 и 2, которые уже встречались в списках. Значит, список вершины 3 будет пустым: … Аналогичным образом составляется список вершины . Повторим полученный набор списков:

(1.7)

Просматривая списки, замечаем что сток (вершина 6) попал в подмножество A. Значит поток XP⁰ не максимален и существует путь из истока в сток, состоящий из ненасыщенных ребер.

Перейдем к п. 3 алгоритма – выделению ненасыщенных ребер пути из истока в сток и преобразованию имеющегося потока в новый поток большей мощности. В списке (1.7) последним ребром (i _n-1, S) является (4, 6), ребром (i B_n-2B, i B_n-1B) – ребро (2, 4), ребром (I, iB_1B) – ребро (1, 2). Найденный путь по ненасыщенным ребрам из истока 1 в сток 6 пройдет через вершины 1, 2, 4 и 6.

Поскольку ненасыщенный путь найден, то следующим шагом является определение с помощью матрицы R – XP⁰ величины , на которую можно увеличить поток по каждому ребру (i, j) выделенного пути, чтобы получить новый поток X¹ мощности, большей на единиц. Как видно из табл. 1.4., по ребру (1, 2) можно дополнительно пропустить 6 ед., по ребру (2, 4) – 4 ед., по ребру (4, 6) – только 2 ед., так что

Для построения матрицы нового потока X¹ к соответствующим элементам x_ij⁰ матрицы XP⁰ прибавляется найденное значение , после чего возвращаются к п. 2 алгоритма, и т.д. до получения максимального потока.

Прибавим величину к элементам x₁₂⁰ = 1, x₂₄⁰ = 0 и x₄₆⁰ = 2, обозначающим ненасыщенный путь (по всем остальным ребрам величина потока не изменится). Приходим к матрице нового потока X¹ (см. табл. 1.5), мощность которого равна 7 ед. Этот поток вновь надо исследовать на оптимальность, т. е. вернуться к п. 2 алгоритма. Вновь составляем матрицу R – X¹ (см. табл. 1.5), а по ней – списки вершин, достижимых из истока I по ненасыщенным путям:

Из этих списков видно, что сток 6 снова в подмножестве A, а путь, ведущий в него, состоит из ненасыщенных ребер (1, 2), (2, 4), (4, 5), (5, 6). Новый поток X², (его матрица представлена в табл. 1.6, получается преобразованием потока X¹, если увеличить на потоки по указанным ребрам найденного ненасыщенного пути. Мощность нового потока X² составляет 9 ед. Для исследования этого потока составляется матрица R – X² (табл. 1.8), а по ней – списки.

 (1.8)

Таблица 1.6

i/j	1	2	3	4	5	6
1	0	5	2	2	0	0
2	-5	0	0	4	1	0
3	-2	0	0	0	2	0
4	-2	-4	0	0	2	4
5	0	-1	-2	-2	0	5
6	0	0	0	-4	-5	0

Таблица 1.7

i/j	1	2	3	4	5	6
1	0	4	2	0	0	0
2	6	0	8	2	0	0
3	8	8	0	0	0	0
4	7	11	0	0	8	0
5	0	6	4	3	0	2
6	0	0	0	10	10	0

По спискам (1.8) видно, что сток 6 не попал в подмножество A вершин, достижимых из истока по ненасыщенным ребрам. Значит поток X² максимален. Нанесем его на сеть с указанием направления потоков по отдельным ребрам (см. рис. 1.11).

Таблица 1.8

i/j	1	2	3	4	5	6
1	0	4	2	0	0	0
2	6	0	8	2	0	0
3	8	8	0	0	0	0
4	7	11	0	0	8	0
5	0	6	4	3	0	2
6	0	0	0	10	10	0

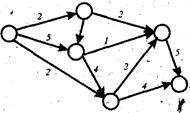
Рис. 1.11

Можно было бы и не строить матрицу R – X², если своевременно заметить, что потоки по ребрам (4, 6) и (5, 6) равны их пропускным способностям, т.е эти ребра насыщены (см. табл. 1.7 и 1.8).

Используя списки (табл. 1.8) выделим подмножества A и B, на которые оказалось разбитым множество всех вершин: A = {1, 2, 3}, B = {4, 5, 6}. Теперь можно выписать ребра, образующие разрез A / B минимальной пропускной способности: (1, 4), (2, 4), (2, 5), (3, 5).

Заключение

Как говорилось выше, теория графов, теория сетей имеют широкое и разнообразное применение. К задаче о максимальном потоке можно, например, свести задачу об оптимальном назначении, хотя такая задача относится к задаче целочисленного программирования и может быть решена соответствующими методами. К задаче о максимальном потоке можно свести транспортную задачу на минимизацию времени перевозок.

Список использованной литературы

 

1.              Акулич Н.А. Математическое программирование в примерах и задачах. – М.: Высшая школа, 2003.

2.              Иозайтис В.С., Львов Ю.А. Экономико-математическое моделирование производственных систем. – М.: Высшая школа, 2000.

3.              Миненко С.Н., Гамазина Г.И. Экономико-математическое моделирование производственных систем. – Учебное пособие, МГИУ