Определим параметры уравнения прямой на основе метода наименьших квадратов, решив систем нормальных уравнений

2. Определим параметры уравнения прямой на основе метода наименьших квадратов, решив систем нормальных уравнений.

(2)

Откуда:

 (3)

(4)

По формулам (3), (4) вычислим а₀, а₁, используя расчетные данные таблицы 2.

.

.

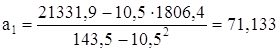Таблица 2 Расчетные данные для линейной парной регрессии

№ п/п	х	у	х2	ух		у-	(у-)2	у2	у-	(у-)2
1	1	1238	1	1238	1131	107,4	11537,8	1532644	-568,4	323021,7
2	2	1185	4	2370	1202	-16,7	279,5	1404225	-621,4	386075,8
3	3	1234	9	3702	1273	-38,9	1509,5	1522756	-572,4	327584,5
4	4	1285	16	5140	1344	-59,0	3479,2	1651225	-521,4	271805,8
5	5	1396	25	6980	1415	-19,1	365,5	1948816	-410,4	168387,1
6	6	1507	36	9042	1486	20,7	430,5	2271049	-299,4	89610,4
7	7	1524	49	10668	1557	-33,4	1114,5	2322576	-282,4	79721,5
8	8	1574	64	12592	1629	-54,5	2972,1	2477476	-232,4	53986,5
9	9	1719	81	15471	1700	19,3	374,4	2954961	-87,3	7630,0
10	10	1804	100	18040	1771	33,2	1103,3	3254416	-2,3	5,5
11	11	1817	121	19987	1842	-24,9	620,8	3301489	10,7	113,4
12	12	1893	144	22716	1913	-20,0	402,0	3583449	86,7	7508,2
13	13	2047	169	26611	1984	62,8	3946,0	4190209	240,7	57912,4
14	14	2137	196	29918	2055	81,7	6672,3	4566769	330,7	109329,4
15	15	2121	225	31815	2126	-5,4	29,7	4498641	314,7	99004,6
16	16	2143	256	34288	2198	-54,6	2979,2	4592449	336,7	113333,2
17	17	2293	289	38981	2269	24,3	589,8	5257849	486,7	236828,2
18	18	2363	324	42534	2340	23,2	536,0	5583769	556,7	309859,2
19	19	2396	361	45524	2411	-15,0	224,4	5740816	589,7	347687,1
20	20	2451	400	49020	2482	-31,1	968,1	6007401	644,7	415573,6
Итого	210	36127	2870	426637	36127,00	0,0	40134,8	68662985,0	0,0	3404978,6
В среднем	10,5	1806,4	143,5	21331,9	1806,4	0,0	2006,7	3433149,3	0,0	170248,9

Вычислив параметры, получим следующее уравнение:

у_х = 1059,5 + 71,1 ∙ х.

Следовательно, с увеличением номера квартала на 1%, величина прожиточного минимума увеличится на 71,1%.

3. Значимость коэффициентов регрессии проверим по t-критерию Стьюдента. Вычислим расчетные значения t-критерия по формулам:

для параметра а₀:

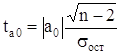 , (5)

для параметра а₁:

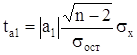 , (6)

где n = 20 - объем выборки,

среднее квадратическое отклонение результативного признака у от выровненных значений у­_х:

, (7)

среднее квадратическое отклонение факторного признака х от общей средней :

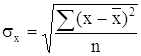. (8)

Находим:

, ,

, .

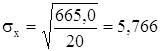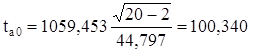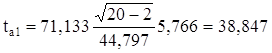Вычисленные значения t_a0 и t_a1 сравнивают с критическими (табличными) t, которые определяют по таблице Стьюдента с учетом принятого уровня значимости а и числом степеней свободы вариации v = n -2 = 20-2 =18. В социально-экономических исследованиях уровень значимости а обычно принимают равным 0,05. Параметр признается значимым при условии, если t_расч> t_табл.

Так как t_расча0 = 100,340 и t_расча1 = 38,847 больше t_табл = 2,101, то параметры а₀ и а₁ признаются значимыми, т.е. в этом случае маловероятно, что найденное значение параметра обусловлено только случайными совпадениями.

Выявим тесноту корреляционной связи между х и у с помощью линейного коэффициента корреляции, используя формулу:

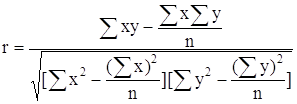.(9)

.

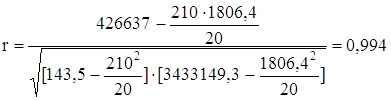Т.к. r =0,994, то связь прямая сильная, полная.

Значимость линейного коэффициента корреляции определяется помощью t-критерия Стьюдента (число степеней свободы равно 18, уровень значимости а=0,05) по формуле:

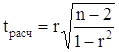. (10)

.

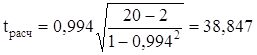Так как = 38,847 больше t_табл = 2,101, следовательно, коэффициент корреляции признается значимым.

Определим линейный коэффициент детерминации r²:

r² = 0,994² = 0,988.

Он показывает, что 98,8% вариации величины прожиточного минимума обусловлено вариацией номера квартала.

Теоретическое корреляционное отношение η определим по формуле:

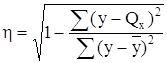. (11)

.

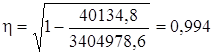Т.к. r = η, то линейная форма связи между у и х выбрана верно. Экономическую интерпретацию модели дополнит коэффициент эластичности:

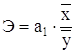. (12)

.

Это значит, что при увеличении номера квартала на 1% величина прожиточного минимума возрастет на 0,41%.

4. Далее используем F-критерий Фишера, чтобы оценить статистическую надежность результатов регрессионного моделирования.

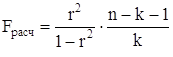. (13)

.

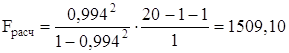Сравнивая полученное значение с табличным, видим, что F_расч > F_табл = 8,6718. Следовательно, в целом, модель значима.

Таким образом, модель признается адекватной и на ее основе можно принимать решения и осуществлять прогнозы.

5. Рассчитаем, чему должно быть равно прогнозное значение величины прожиточного минимума в 1 квартале 2005 года, во 2 квартале 2007 года, используя уравнение регрессии:

у_х = 1059,5 + 71,1 ∙ х.

1-ый квартал 2005 года имеет номер 21; 2-ый квартал 2007 года - 30.

Подставив эти значения в уравнения регрессии, получим:

- прогнозное значение для 1-го квартала 2005 года:

у_х = 1059,5 + 71,1 ∙ 21 = 2553,2 руб.;

- прогнозное значение для 2-го квартала 2007 года:

у_х = 1059,5 + 71,1 ∙ 30 = 3193,4 руб.

6. Определим доверительный интервал 2-ого прогноза для уровня значимости, равного 0,05.

Рассчитаем интегральную ошибку прогноза - Е_Y, которая формируется как сумма двух ошибок: из ошибки прогноза как результата отклонения прогноза от уравнения регрессии - S²_Y и ошибки прогноза положения регрессии - µ_Y. То есть:

.

В нашем случае

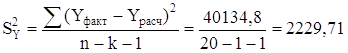
где k - число факторов в уравнении, которое в данной задаче равно 1.

Тогда = 47,22 руб.

Ошибка положения регрессии составит:

.

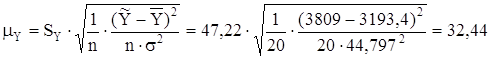 32,44.

Интегральная ошибка прогноза составит:

 руб.

Предельная ошибка прогноза, которая не будет превышена в 95% возможных реализаций прогноза, составит:

∆Y = t_табл ∙ Е_Y = 2,101 ∙ 57,29 = 120,37 руб.

Следовательно, ошибка большинства реализаций прогноза не превысит ±120,37 руб.

Это означает, что фактическая реализация прогноза будет находиться в доверительном ин­тервале γ = Y ± ∆Y.

Нижняя граница доверительного интервала составит:

γ_min = Y - ∆Y = 3809,0 - 120,37 = 2760,2 руб.

Верхняя граница доверительного интервала составит:

γ_max = Y + ∆Y = 3809,0 + 120,37 = 3313,8 руб.

Доверительный интервал:

.

3073,13313,8.

7. Сравним полученный результат с реальной ситуацией.

Во 2-м квартале 2007 г. официальный прожиточный минимум в России составил 3809 руб., то есть на 19,28% больше, чем в среднем по нашим расчетам и на 13,57% больше верхней границы доверительного интервала.

Такое расхождение указывает, что надежная применимость полученного уравнения регрессии ограничена ближайшими будущими кварталами.

Литература

1. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов вузов. Изд 4-е, стер. - М.: Высш. шк., 1998. - 400 с.

2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч. Ч. II: Учеб. пособие для втузов. - 5-е изд., испр. - М.: Высш. шк., 1997. - 416 с.

3. Карасев А.И., Аксютина З.М., Савельева Т.И. Курс высшей математики для экономических вузов. В 2-х частях. Ч. II. Теория вероятностей и математическая статистика. Линейное программирование. - М.: Высшая школа, 1982.

4. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. - М.: Наука, 1986.

5. Гмурман В.Е. Теории вероятностей и математическая статистика: Учеб. пособие для вузов. Изд 6-е, стер. -М.: Высш. шк.,1998. - 479 с.

6. Кремер Н.Ш. Математическая статистика. Учебное пособие/ ВЗФЭИ. - М.: Экономическое образование, 1992. - 112 с.

7. Вентцель Е.С. Теория вероятностей: Учеб. для вузов. - 5-е изд. стер. - М.: Высш. шк., 1998. - 576 с.