Навигация
Теснота связи между фактором и откликом
1. Теснота связи между фактором и откликом
Мерой тесноты связи служит линейный коэффициент корреляции:
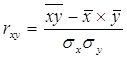 (2.13)
(2.13)
-1 £ rxy £ 1 (2.14)
Отрицательное значение КК означает, что увеличение фактора приводит к уменьшению отклика и наоборот:
![]()
![]()
2. Доля вариации отклика у, объясненная полученным уравнением регрессии характеризуется коэффициентом детерминации R2. Путем математических преобразований можно выразить:
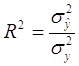
где – оценка дисперсии случайных остатков в модели,
Таким образом, R2 – это доля дисперсии у, объясненной с помощью регрессионного уравнения в дисперсии фактически наблюденного у.
Очевидно:
0 £ R2 £ 1
3. Проверка статистической значимости уравнения регрессии
Мы получили МНК-оценки коэффициентов уравнения регрессии и рассчитали коэффициент детерминации. Однако, осталось неясным, достаточно ли он велик, чтобы говорить о существовании значимой связи между величинами х и у. Иначе говоря, достаточно ли сильна эта связь, чтобы на основании построенной нами модели можно было бы делать выводы?
Для ответа на этот вопрос можно провести т. н. F-тест.
Формулируется гипотеза Н0: предположим, что yi ¹ a + bxi + ei
Обратить внимание: выписаны не а, а a, т. е., не оценки коэффициентов регрессии, а их истинные значения.
Альтернатива – гипотеза Н1: yi = a + bxi + ei
Мы не можем однозначно подтвердить или опровергнуть гипотезу Н0, мы можем лишь принять или отвергнуть ее с определенной вероятностью.
Выберем некоторый уровень значимости g, такой что 0 £ g £ 1 – вероятность того, что мы сделаем неправильный вывод, приняв или отклонив гипотезу Н0.
Соответственно, величина Р = 1 - g - доверительная вероятность – вероятность того, что мы в итоге сделаем правильный вывод.
Для проверки истинности гипотезы Н0, с заданным уровнем значимости g, рассчитывается F-статистика:
Значение F-статистики в случае парной регресии подчиняется т. н.
F-распределению Фишера с 1 степенью свободы числителя и (n - 2) степенями свободы знаменателя.
Для проверки Н0 величина F-статистики сравнивается с табличным значением Fg(1, n-2).
Если F > Fg(1, n-2) – гипотеза Н0 отвергается, т. е. мы считаем, что с вероятностью 1-g можно утверждать, что регрессия имеет место и:
yi = a + bxi + ei
В противном случае гипотеза Н0 не отвергается, принимаем:
yi ¹ a + bxi + ei
Вопрос: почему бы нам не взять g поменьше? Чем меньше g, тем больше соответствующее табличное значение F-статистики, т. е., тем меньше шансов, что появятся основания отвергнуть гипотезу Н0.
Ошибки первого и второго родаОшибка первого рода: отвергается Н0, которая на самом деле верна.
Ошибка второго рода: принимается H0, которая на самом деле не верна.
Очевидно, чем меньше g, тем меньше наши шансы отвергнуть гипотезу Н0, т. е., совершить ошибку первого рода. Соответственно, шансы совершить ошибку второго рода увеличиваются.
4. Характеристика оценок коэффициентов уравнения регрессии
1) математическое ожидание
Теорема: М(а) = a, M(b) = b - несмещенность оценок
Это означает, что при увеличении количества наблюдений значения МНК-оценок a и b будут приближаться к истинным значениям a и b;
2) дисперсия
Теорема:
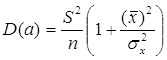 ;
; 
Благодаря этой теореме, мы можем получить представление о том, как далеко, в среднем, наши оценки a и b находятся от истинных значений a и b.
Необходимо иметь в виду, что дисперсии характеризуют не отклонения, а «отклонения в квадрате». Чтобы перейти к сопоставимым значениям, рассчитаем стандартные отклонения a и b:
 ;
; 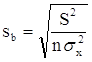
Будем называть эти величины стандартными ошибками a и b соответственно.
5. Построение доверительных интервалов
Пусть мы имеем оценку а. Реальное значение коэффициента уравнения регрессии a лежит где-то рядом, но где точно, мы узнать не можем. Однако, мы можем построить интервал, в который это реальное значение попадет с некоторой вероятностью. Доказано, что:
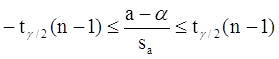
с вероятностью Р = 1 - g
где tg/2(n-1) - g/2-процентная точка распределения Стьюдента с (n-1) степенями свободы – определяется из специальных таблиц.
При этом уровень значимостиg устанавливается произвольно.
Неравенство можно преобразовать следующим образом:
![]()
![]()
![]() ,
,
или, что то же самое:
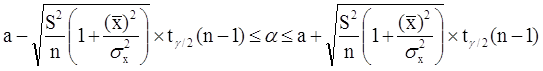
Аналогично, с вероятностью Р = 1 - g:

откуда следует:
![]() ,
,
или:
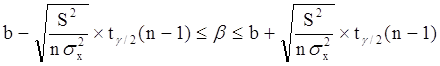
Уровень значимости g - это вероятность того, что на самом деле истинные значения a и b лежат за пределами построенных доверительных интервалов. Чем меньше его значение, тем больше величина tg/2(n-1), соответственно, тем шире будет доверительный интервал.
Похожие работы
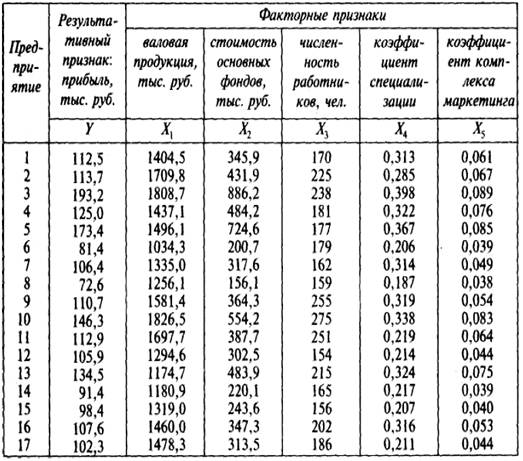
... 9472;───────┴─────────┘ Реализация алгоритма многомерного регрессионного анализа начинается с расчета важнейших статистических характеристик исходной информации и матрицы выборочных парных коэффициентов корреляции. Рассмотрим более подробно вариационные характеристики переменной у: ...
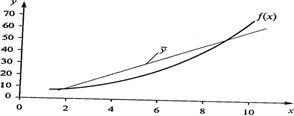
... ŷ = a0 + a1x , где ŷ - теоретические значения результативного признака, полученные по уравнению регрессии; a0 , a1 - коэффициенты (параметры) уравнения регрессии. Задача регрессионного анализа состоит в построении модели, позволяющей по значениям независимых показателей получать оценки значений зависимой переменной. Регрессионный анализ является основным средством исследования ...
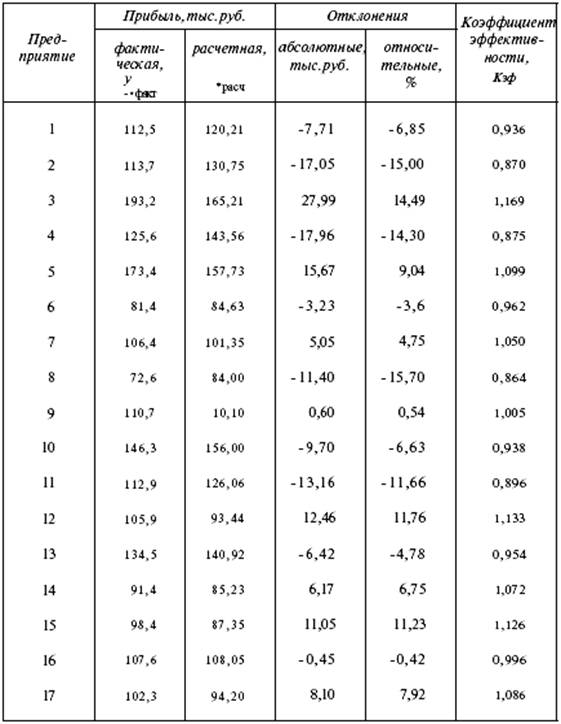
... рассматриваемый период можно признать успешной. 3 Парная линейная регрессия Для характеристики влияния изменений Х на вариацию У служат методы регрессионного анализа. В случае парной линейной зависимости строится регрессионная модель Уi = a0 +a1 *Xi + εi, I=1, …,n где n — число наблюдений; a0 ,a1 — неизвестные параметры уравнения; εi, — ошибка случайной переменной У. ...
... на зависимую и определение расчётных значений зависимой переменной (функции регрессии). Решение всех названных задач приводит к необходимости комплексного использования этих методов. Корреляционный и регрессионный анализ. Исследование связей в условиях массового наблюдения и действия случайных факторов осуществляется, как правило, с помощью экономико-статистических моделей. В широком смысле ...
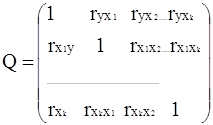

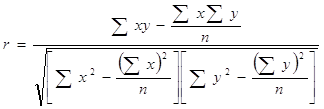
0 комментариев