Навигация
Регрессионный анализ. Транспортная задача
Регрессионный анализ
Задача
Некоторая фирма занимается поставками различных грузов на короткие расстояния внутри города. Необходимо оценить стоимость таких услуг, зависящую от затрачиваемого на поставку времени. В качестве наиболее важного фактора, влияющего на время доставки, выбрано пройденное расстояние. Были собраны исходные данные о десяти поставках (табл.).
| Расстояние, км | 3,5 | 2,4 | 4,9 | 4,2 | 3,0 | 1,3 | 1,0 | 3,0 | 1,5 | 4,1 |
| Время, мин | 16 | 13 | 19 | 18 | 12 | 11 | 8 | 14 | 9 | 16 |
Постройте график исходных данных, определите по нему характер зависимости между расстоянием и потраченным временем, постройте уравнение регрессии, проанализируйте силу регрессионной связи и сделайте прогноз поездки на 2 км.
Решение
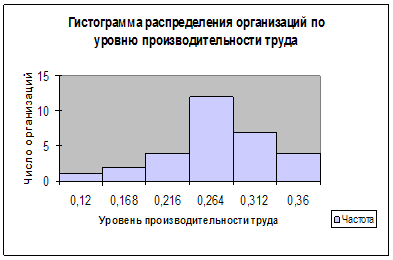
Для расчёта стоимости услуг, зависящих от затрачиваемого на поставку времени, вычислим суммы (рис. 1):
| t | y(t) | | ||||||||||||
|
|
|
|
|
|
| ||||||||
| 1 | 3,50 | 16,00 | 12,25 | 56,00 | 256,00 | 15,22 | 2,63 | |||||||
| 2 | 2,40 | 13,00 | 5,76 | 31,20 | 169,00 | 12,30 | 1,70 | |||||||
| 3 | 4,90 | 19,00 | 24,01 | 93,10 | 361,00 | 18,95 | 28,58 | |||||||
| 4 | 4,20 | 18,00 | 17,64 | 75,60 | 324,00 | 17,08 | 12,14 | |||||||
| 5 | 3,00 | 12,00 | 9,00 | 36,00 | 144,00 | 13,89 | 0,09 | |||||||
| 6 | 1,30 | 11,00 | 1,69 | 14,30 | 121,00 | 9,37 | 17,88 | |||||||
| 7 | 1,00 | 8,00 | 1,00 | 8,00 | 64,00 | 8,57 | 25,27 | |||||||
| 8 | 3,00 | 14,00 | 9,00 | 42,00 | 196,00 | 13,89 | 0,09 | |||||||
| 9 | 1,50 | 9,00 | 2,25 | 13,50 | 81,00 | 9,90 | 13,67 | |||||||
| 10 | 4,10 | 16,00 | 16,81 | 65,60 | 256,00 | 16,82 | 10,36 | |||||||
| сумма |
|
|
|
|
|
|
| |||||||
| 13,60 | ||||||||||||||
| a1 = | 2,66 | |||||||||||||
| a0 = | 5,91 | |||||||||||||
| r2 = | 0,92 | 91,83% | ||||||||||||
| 8,17 |
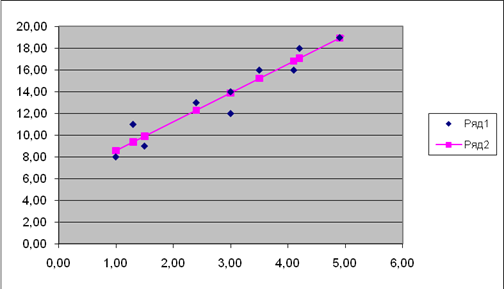
Рис .1 - График исходных данных
Вывод: существует сильная связь между исходными данными.
Задача
В таблице приведены данные по объемам собранного урожая овощей из тепличного хозяйства за последний год (по месяцам), а также данные о затраченной электроэнергии, воде и удобрениях.
| Месяц | Объем собранного урожая | Факторы, влияющие на урожай | ||
| Электроэнергия, кВт | Удобрения, тонн | Вода, литр | ||
| t | y | x1 | x2 | x3 |
| январь | 140 | 165 | 138 | 134 |
| февраль | 138 | 164 | 139 | 128 |
| март | 158 | 158 | 157 | 168 |
| апрель | 144 | 159 | 142 | 147 |
| май | 142 | 148 | 144 | 146 |
| июнь | 134 | 152 | 136 | 140 |
| июль | 122 | 143 | 122,5 | 132 |
| август | 125 | 146 | 128 | 135 |
| сентябрь | 124 | 148 | 119 | 125 |
| октябрь | 138 | 150 | 142 | 126 |
| ноябрь | 157 | 156 | 159 | 143 |
| декабрь | 161 | 160 | 164 | 150 |
Необходимо определить степень влияния каждого отдельного фактора на результат (объем урожая). Для этого необходимо построить графики исходных данных, построить уравнения регрессии, проанализировать силу регрессионной связи (по коэффициенту детерминации) и сделать прогноз урожая по двум-трем значениям (в пределах прогноза исходных данных).
Решение
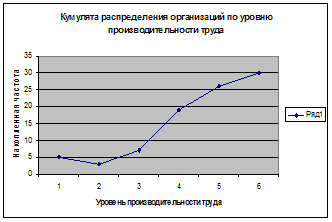
Строим графики исходных данных (рис. 2, 3):
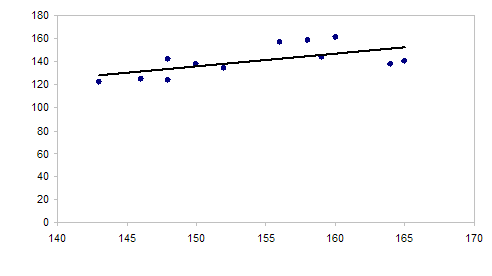
Рис. 2 - График зависимости урожая от удобрения
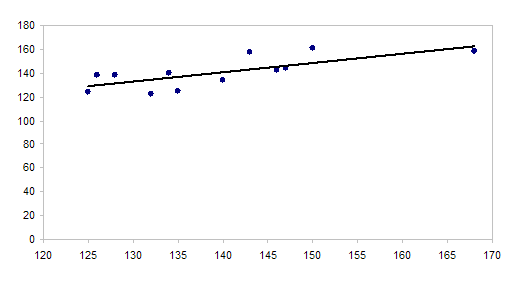
Рис. 3 - График зависимости урожая от воды
Численные коэффициенты функции регрессии для первой зависимости:
Численные коэффициенты функции регрессии
| X1i | Yi | X1i² | X1i Yi | Yi ² | Yip | (Yip -y)² | (Yi -y)² |
| 165 | 140 | 27225 | 23100 | 19600 | 152,5778 | 151,9747 | 0,0625 |
| 164 | 138 | 26896 | 22632 | 19044 | 151,4485 | 125,4073 | 5,0625 |
| 158 | 158 | 24964 | 24964 | 24964 | 144,673 | 19,56251 | 315,0625 |
| 159 | 144 | 25281 | 22896 | 20736 | 145,8022 | 30,82711 | 14,0625 |
| 148 | 142 | 21904 | 21016 | 20164 | 133,3803 | 47,19267 | 3,0625 |
| 152 | 134 | 23104 | 20368 | 17956 | 137,8974 | 5,534888 | 39,0625 |
| 143 | 122 | 20449 | 17446 | 14884 | 127,734 | 156,6506 | 333,0625 |
| 146 | 125 | 21316 | 18250 | 15625 | 131,1218 | 83,32442 | 232,5625 |
| 148 | 124 | 21904 | 18352 | 15376 | 133,3803 | 47,19267 | 264,0625 |
| 150 | 138 | 22500 | 20700 | 19044 | 135,6388 | 21,26283 | 5,0625 |
| 156 | 157 | 24336 | 24492 | 24649 | 142,4144 | 4,684729 | 280,5625 |
| 160 | 161 | 25600 | 25760 | 25921 | 146,9315 | 44,64219 | 430,5625 |
| 1849 | 1683 | 285479 | 259976 | 237963 | 738,2566 | 1922,25 | |
| Среднее значение | 140,25 |
Коэффициент детерминации r2=0,384059.
Коэффициент детерминации низкий поэтому модель не адекватна.
Численные коэффициенты функции регрессии для первой зависимости, представляем расчеты виде таблицы:
Численные коэффициенты функции регрессии
| X2i | Yi | X2i² | X2i Yi | Yi ² | Yip | (Yip -y)² | (Yi -y)² |
| 138 | 140 | 19044 | 19320 | 19600 | 137,5802 | 7,127725 | 0,0625 |
| 139 | 138 | 19321 | 19182 | 19044 | 138,5088 | 3,031641 | 5,0625 |
| 157 | 158 | 24649 | 24806 | 24964 | 155,224 | 224,2202 | 315,0625 |
| 142 | 144 | 20164 | 20448 | 20736 | 141,2947 | 1,091391 | 14,0625 |
| 144 | 142 | 20736 | 20448 | 20164 | 143,1519 | 8,421225 | 3,0625 |
| 136 | 134 | 18496 | 18224 | 17956 | 135,723 | 20,49389 | 39,0625 |
| 122,5 | 122 | 15006,25 | 14945 | 14884 | 123,1866 | 291,1588 | 333,0625 |
| 128 | 125 | 16384 | 16000 | 15625 | 128,294 | 142,9452 | 232,5625 |
| 119 | 124 | 14161 | 14756 | 15376 | 119,9365 | 412,64 | 264,0625 |
| 142 | 138 | 20164 | 19596 | 19044 | 141,2947 | 1,091391 | 5,0625 |
| 159 | 157 | 25281 | 24963 | 24649 | 157,0812 | 283,29 | 280,5625 |
| 164 | 161 | 26896 | 26404 | 25921 | 161,7243 | 461,1463 | 430,5625 |
| 1690,5 | 1683 | 240302,3 | 239092 | 237963 | 1856,658 | 1922,25 | |
| Среднее значение | 140,25 |
Коэффициенты регрессии — сдвиг а0 и наклон а1 прямой у:
| a0= | 9,430782 |
| a1= | 0,928619 |
Коэффициент детерминации r2=0,965877.
Коэффициент детерминации высокий, поэтому модель адекватна и можно делать прогноз.
Прогноз на три шага вперед y13=120.9, y14=154.3, y15=142.2.
Численные коэффициенты функции регрессии для первой зависимости, представляем расчеты виде таблицы:
Численные коэффициенты функции регрессии
| X3i | Yi | X3i² | X3i Yi | Yi ² | Yip | (Yip -y)² | (Yi -y)² |
| 134 | 140 | 17956 | 18760 | 19600 | 135,8979 | 18,94079 | 0,0625 |
| 128 | 138 | 16384 | 17664 | 19044 | 131,1502 | 82,80727 | 5,0625 |
| 168 | 158 | 28224 | 26544 | 24964 | 162,8018 | 508,5838 | 315,0625 |
| 147 | 144 | 21609 | 21168 | 20736 | 146,1847 | 35,22048 | 14,0625 |
| 146 | 142 | 21316 | 20732 | 20164 | 145,3934 | 26,4545 | 3,0625 |
| 140 | 134 | 19600 | 18760 | 17956 | 140,6456 | 0,156535 | 39,0625 |
| 132 | 122 | 17424 | 16104 | 14884 | 134,3153 | 35,22048 | 333,0625 |
| 135 | 125 | 18225 | 16875 | 15625 | 136,6892 | 12,67937 | 232,5625 |
| 125 | 124 | 15625 | 15500 | 15376 | 128,7763 | 131,6463 | 264,0625 |
| 126 | 138 | 15876 | 17388 | 19044 | 129,5676 | 114,1144 | 5,0625 |
| 143 | 157 | 20449 | 22451 | 24649 | 143,0195 | 7,670238 | 280,5625 |
| 150 | 161 | 22500 | 24150 | 25921 | 148,5586 | 69,03215 | 430,5625 |
| 1674 | 1683 | 235188 | 236096 | 237963 | 1042,526 | 1922,25 | |
| Среднее значение | 140,25 |
Коэффициенты регрессии — сдвиг а0 и наклон а1 прямой у:
| a0= | 29,86486 |
| a1= | 0,791291 |
Коэффициент детерминации r2=0,542347.
Коэффициент детерминации низкий, поэтому модель не адекватна.
Задача
Санаторный комплекс ежегодно заключает с пекарней договор на выпечку хлеба сорта С1. Чтобы полностью использовать свои производственные мощности пекарня также выпекает хлеб сорта С2, который пускает в свободную продажу. В таблице приведены данные выпуска хлеба (тыс. шт.) пекарней за последний год
| Месяц | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| С1 | 1 | 2,3 | 1,5 | 0,5 | 4 | 5 | 2 | 3,5 | 1 | 4,5 | 2,5 | 1,5 |
| С2 | 9 | 6,5 | 8,1 | 8,7 | 4 | 0,2 | 7,6 | 5 | 8,7 | 2 | 7 | 8,4 |
Проанализируйте график исходных данных и постройте регрессионную модель функции производственных возможностей пекарни. Проверьте удовлетворительность модели и сделайте прогноз выпуска хлеба С2, если санаторный комплекс сделает заказ хлеба С1
Похожие работы
... модели меньше ошибка, но в первой лучше показатели качества регрессионного уравнения, более того, вторая модель неадекватна, т.е. не соответствует исходным данным и оценкам, полученным при помощи регрессионного анализа и регрессионная модель отражает анализируемые данные не точно. Следовательно, более точной является первая модель. Таким образом, модель зависимости уровня рентабельности от числа ...
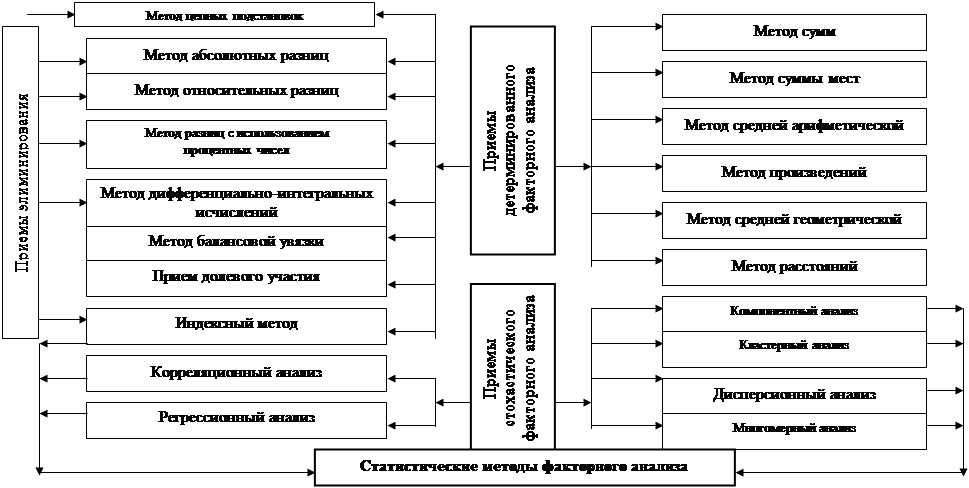
... группы, установление связи и ее направление. Индексный метод является гибким аналитическим инструментом и может применяться в анализе показателе производственной, финансовой, инвестиционной и других видах деятельности предприятия (фирмы). Корреляционный и регрессионный анализ являются довольно сложной операцией. Исходными предпосылками для их проведения являются: случайный характер факторов, ...
... , а в предыдущие периоды происходило снижение. Таким образом, по результатам проведенного анализа мы видим ухудшение основных показателей деятельности внутреннего водного транспорта в РФ. 2.2 Оценка структуры и динамики структуры экономико-статистических показателей внутреннего водного транспорта Далее проведем анализ структуры и динамики структуры основных показателей развития внутреннего ...
... объектов; б) наличие данных за предыдущий период; в) наличие базисных данных; г) сопоставимость данных. 26. По характеру принимаемых решений экономический анализ подразделяется: а) предварительный, текущий и заключительный б) оперативный, ретроспективный и перспективный в) предварительный, последующий и итоговый 27. Информация, ...
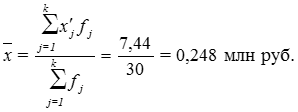
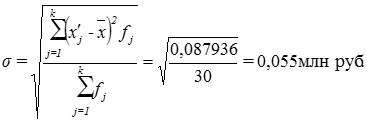
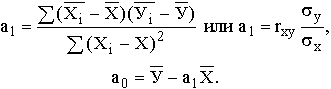

0 комментариев