Навигация
Решение задачи линейного программирования симплекс-методом
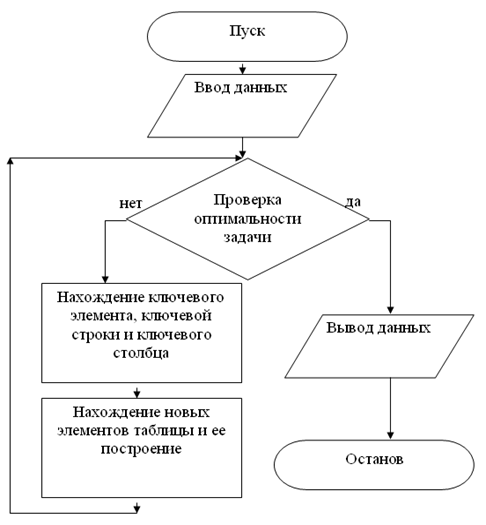
3. Решение задачи линейного программирования симплекс-методом.
Двойственная задача.
Составим двойственную задачу по условиям прямой задачи и определим области допустимых решений ДП:
Прямая задачаДвойственная задача
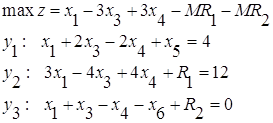
![]()
![]()
![]()
![]() (1)
(1)
![]() (2)
(2)
![]()
![]()
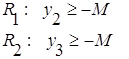
Итак, получено: ![]() ,
, ![]() ,
, ![]() .
.
2. Приведём запись двойственной задачи к канонической форме. На основании полученных ОДР двойственных переменных введём необходимые подстановки: ![]() .
.
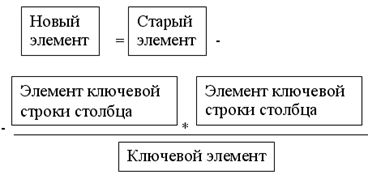
Для удобства решения свернём ограничения (1) и (2) в одно со знаком равенства, а также введем в ограничения и целевую функцию избыточные, остаточные и искусственные переменные.
![]()
![]() (3)
(3)
![]() (4)
(4)
3. Решим ДЗ симплекс методом:
Из (3): выразим![]()
Из (4) выразим: ![]()
![]()
![]() СТ(0)
СТ(0)
| W |
|
|
|
|
|
|
| ПЧ | |
| W | 1 | -4-M | 7M-12 | 12-7M | 0 | -M | 0 | 0 | 4M |
|
| 0 | 1 | 3 | -3 | -1 | -1 | 1 | 0 | 1 |
|
| 0 | -2 | 4 | -4 | 1 | 0 | 0 | 1 | 3 |
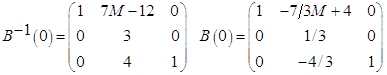
СТ(1)
| W |
|
|
|
|
|
|
| ПЧ | |
| W | 1 | -10/3M | 0 | 0 | 7/3M-4 | 4/3M-4 | -7/3M+4 | 0 | 5/3M+4 |
|
| 0 | 1/3 | 1 | -1 | -1/3 | -1/3 | 1/3 | 0 | 1/3 |
|
| 0 | -10/3 | 0 | 0 | 7/3 | 4/3 | -4/3 | 1 | 5/3 |
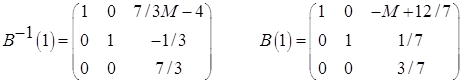
СТ(2)
| W |
|
|
|
|
|
|
| ПЧ | |
| W | 1 | -40/7 | 0 | 0 | 0 | -12/7 | -7/3M+4 | -M+12/7 | 48/7 |
|
| 0 | -1/7 | 1 | -1 | 0 | -1/7 | 1/3 | 1/7 | 4/7 |
|
| 0 | -10/7 | 0 | 0 | 1 | 4/7 | -4/3 | -3/7 | 5/7 |
СТ(2) – оптимальная, т. к. коэффициенты при ![]()
![]() ,
, ![]() ,
,
![]()
Задание:
1. Изучить методы решения задачи линейного программирования (графический и симплекс-метод):
2. Для заданного варианта получить решение задачи линейного программирования:
- графическим методом;
- симплекс методом для прямой задачи;
- симплекс методом для двойственной задачи.
Похожие работы
... положит в такой симплекс-таблице текущие базисные переменные равными Ai,0, а свободные - нулю, то будет получено оптимальное решение. Практика применения симплекс метода показала, что число итераций, требуемых для решения задачи линейного программирования обычно колеблется от 2m до 3m, хотя для некоторых специально построенных задач вычисления по правилам симплекс метода превращаются в прямой ...
... и подставляя её во всех остальных равенствах и неравенствах (а также в функции f).Такую задачу называют «основной» или «стандартной» в линейном программировании. 1.2 Решение задач линейного программирования симплекс-методом Задача ЛП в общем виде может быть записана так: (c, x) − max Ax = b, где c =(c1,c2,...,cn)T – мерный вектор-столбец коэффициентов; x =(x1,x2,...,xn)T – ...
... 0 505/103 0 792/103 669/103 500/103 Анализ Таблицы 6 позволяет сделать вывод о допустимости и оптимальности базиса XБ4=(x5, x7, x1, x2, x4)T. 3.4 Результат решения задачи планирования производства В результате решения поставленной задачи симплекс-методом получили набор производимой продукции x=(x1, x2, x3, x4, x5)=( 15145/103, 8910/103, 0, 1250/103, 3255/103), который удовлетворяет всем ...
... - формула (1.2), ограничений не отрицательности переменных (есть, нет) - формула (1.3) (1.1) i = 1,… m (1.2) (1.3) Алгоритм решения задач линейного программирования требует приведения их постановки в канонический вид, когда целевая функция ...
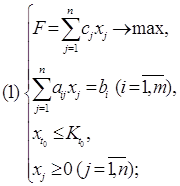
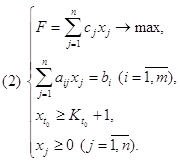
0 комментариев