Навигация
Рассмотреть те же вопросы для случая произвольного линейного оператора
2. Рассмотреть те же вопросы для случая произвольного линейного оператора.
§2 Структура графа состояний для линейного оператора над Zp
Введение
Рассмотрим множество ![]() и линейный оператор
и линейный оператор ![]() такое, что y – линейный оператор над полем Zp, в частности, этот оператор может задавать изменение состояния некоторого одномерного клеточного автомата с p состояниями.
такое, что y – линейный оператор над полем Zp, в частности, этот оператор может задавать изменение состояния некоторого одномерного клеточного автомата с p состояниями.
Будем рассматривать граф состояний ![]() , для которого
, для которого ![]() . Основной целью исследования является изучение структуры графа
. Основной целью исследования является изучение структуры графа ![]() .
.
Одним из важных свойств оператора y, которое будет использоваться в дальнейшем, является его аддитивность:
![]()
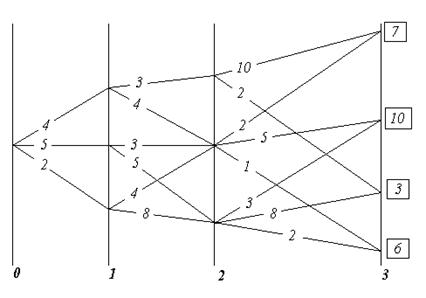
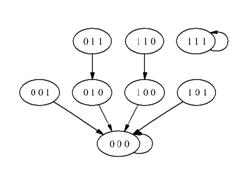
Для исследования структуры графа Gyрассмотрим следующую нумерацию вершин нулевого дерева (см. рис. 2.1).
![]() – вершина, находящаяся на m ярусе, при этом она входит в
– вершина, находящаяся на m ярусе, при этом она входит в ![]()
(![]() ), смысл этих обозначений станет ясным позже. Важно то, что в этих обозначениях в вершину
), смысл этих обозначений станет ясным позже. Важно то, что в этих обозначениях в вершину ![]() входят
входят ![]() , при этом вершины
, при этом вершины ![]() входят в
входят в ![]() (в нашем случае.
(в нашем случае.
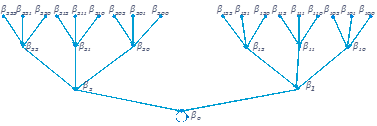
Рис. 2.1
Теорема 2.1
Пусть задана цепь: ![]() тогда
тогда ![]() .
.
Доказательство:
Воспользуемся методом математической индукции.
База m=1:
![]()
![]() , действительно
, действительно ![]() причем
причем ![]() различные вершины, ч.т.д.
различные вершины, ч.т.д.
Пусть теорема верна для m = l-1, т.е![]() .
.
Докажем, что ![]() Тем, самым, по построению
Тем, самым, по построению ![]() , мы покажем, что
, мы покажем, что ![]() .
.
Действительно, в силу линейности![]() :
:
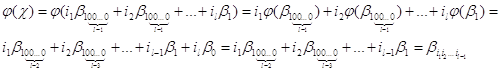
Теорема 2.1 доказана.
Назовем дерево с корнем en = (0,0,…,0) – «нулевым» деревом, тогда для него верна следующая теорема.
Теорема 2.2
«Нулевое» дерево – p-нарное дерево с точностью до петли в корне (0,0..,0).
Доказательство:
По теореме 2.1 единственная цепь из висячей вершины в (0,0,..0) однозначным образом определяет все элементы дерева (различность определяемых вершин очевидна, и следует из простоты p).
Теорема 2.3
Каждое дерево притягиваемого каждой точкой каждого цикла графа Gy изоморфно нулевому» дереву.
Доказательство:
Для любых последовательностей k и l, находящихся на одном ярусе какого-то дерева, для которых выполняется условие:

верно равенство:
![]() ,
,
где ![]() ―одна из последовательностей «нулевого» дерева на n-ном ярусе (сумма в поле
―одна из последовательностей «нулевого» дерева на n-ном ярусе (сумма в поле ![]() ) (Следует из теоремы 2.1).
) (Следует из теоремы 2.1).
Используя полученное соотношение можно достроить любое дерево до дерева изоморфного «нулевому».
§3 ACS-автомат §3.1 Постановка задачи
В данной работе рассматривается клеточный автомат (одномерный), функционирование которого осуществляется по следующим правилам:
Дана полоска 1![]() n (сам автомат), все клетки, которой находятся в состояниях «0» и «1». Изменение состояния клетки определяется следующим образом: данная клетка переходит в состояние «1», если её соседи находятся в разных состояниях, и в «0»,если её соседи находятся в одинаковых состояниях. Клетки, находящиеся по краям переходят в то же состояние, которое было у единственной соседней клетки в предыдущий момент времени.
n (сам автомат), все клетки, которой находятся в состояниях «0» и «1». Изменение состояния клетки определяется следующим образом: данная клетка переходит в состояние «1», если её соседи находятся в разных состояниях, и в «0»,если её соседи находятся в одинаковых состояниях. Клетки, находящиеся по краям переходят в то же состояние, которое было у единственной соседней клетки в предыдущий момент времени.
По полоске длины n будем определять вектор ![]() , где
, где ![]() :
:
![]()
Рассмотрим множество ![]() и отображение
и отображение ![]() такое, что
такое, что

(здесь и ниже ![]() – операция сложения по mod p=2, т.е. операция сложения в поле Z2).
– операция сложения по mod p=2, т.е. операция сложения в поле Z2).
Будем рассматривать граф состояний ![]() , для которого
, для которого ![]() . Основной целью исследования является изучение структуры графа
. Основной целью исследования является изучение структуры графа ![]() .
.
Для начала рассмотрим некоторые определения и обозначения, которые будут использоваться в дальнейшем в работе:
· Ориентированное дерево — это ориентированный граф без циклов, в котором из каждой вершины, кроме одной, называемой корнем ориентированного дерева, выходит ровно одно ребро (более подробно структуры дерева будет определена позже).
· m-й ярус – множество вершин дерева, находящихся на расстоянии m от корня.
· Частичный порядок на вершинах: ![]() , если вершины u и v различны и вершина u лежит на единственном элементарном пути, соединяющем вершиной v с корнем дерева.
, если вершины u и v различны и вершина u лежит на единственном элементарном пути, соединяющем вершиной v с корнем дерева.
· Корневое поддерево с корнем v — подграф ![]() .
.
· Множество ![]() назовем множеством висячих вершин графа
назовем множеством висячих вершин графа ![]() .
.
В прошлом году на ряде конференций (см. Используемые источники) была представлена работа по клеточным автоматам, в которой был исследован частный случай линейного оператора и найдены высоты деревьев для последовательностей, состоящих из 2n-1 элементов. В ней были представлены следующие утверждения, которые будут использоваться в дальнейшем:
Утверждение 3.2.1
![]() .
.
Утверждение 3.2.2
1. ![]() ;
;
2. ![]() , причем
, причем ![]()
![]()
3. ![]() ;
;
4. ![]() .
.
Утверждение 3.2.3
![]() ;
; ![]() и
и ![]() .
.
Предисловие
В параграфе будет рассказано о свойствах графа состояний оператора j, а именно будет описана его структура.
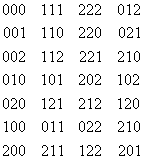
§3.3 Структура Gj при p=2 §3.3.1 Исследование структурыПользуясь утверждением 3.2.2, мы получаем, что среди всех последовательностей можно выделить следующие:
Похожие работы
... за собой её гибель, либо требующие подключения к процессу самоуправления суперсистемы иерархически высшего управления. Так соборный интеллект видится индивидуальному интеллекту с точки зрения достаточно общей теории управления; возможно, что кому-то всё это, высказанное о соборных интеллектах, представляется бредом, но обратитесь тогда к любому специалисту по вычислительной технике: примитивная ...
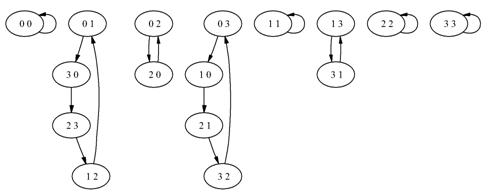
... 000 - , 001 - , 010 - , 011 - , 100 - , 101 - , 110 - , 111 - . Фазовое пространство изображено на рисунке 1.2.3. Рис. 1.2.3. Фазовое пространство . Теорема 1.2.1. Пусть – мономиальная динамическая система. Тогда – система конечных элементов тогда, и только тогда, когда и – системы конечных элементов. Доказательство. Из следствий 1.2.1 и 1.2.3, если – система конечных ...
... все содержание посылок, поскольку оно необходимо для вывода, имеет нечувственный характер. (аксиомы, постулаты). VI. Интуитивизм, индивидуалистический эмпиризм и априоризм критической философии в их отношении к теории элементарных методов знания. Три ответа на вопрос о происхождении общих суждений: 1) Путем прямых методов (прямой индукции) = интуитивизм. 2) Общих суждений нет Только иллюзия. ( ...
... Замечат. С.: Полемон, Герод Аттик, Аристид, Либаний. Ср. Schmid, "Der Atticismus in seinen Hauptvertretern" (1887-97). 17. Принцип детерминизма в философии. Индетерминизм. Детерминизм (от лат. determino - определяю), философское учение об объективной закономерной взаимосвязи и взаимообусловленности явлений материального и ...

0 комментариев