Навигация
1. Постановка проблеми.
Раді Геометрів були запропоновані задачі по знаходженню площ многокутників. Вони у них спричиняли велику скруту. Не прийшовши до єдиної думки, Геометри вирішили спорядити експедиції на острів Площ, де за переказами знаходиться ключ до вирішення даних задач. Спонсорувати дані експедиції буде (вчитель називає себе, передає всі події, події під час плавання на острів).
Метою даної експедиції є пошук ключа, за допомогою якого можна буде вирішити задачі.
Вам належить сформувати дві команди, вибрати капітанів, придумати девіз, під яким команди відправляться в подорож.
(Дається час на обдумування).
У таке відповідальне плавання вирішила відправитися команда . . . на чолі з капітаном . . ., девізом якої є . . . і команда.
2. Підготовка спорядження.(Фронтальна робота)
Ученикам роздається матеріал із завданням і відкривається відповідний матеріал на дошці.
Перед плаванням всі учасники експедиції перевіряють свою готовність: «Закрили очі, пригадали всі формули для знаходження площ багатокутників і привели свої думки в порядок. Розплющили очі і відповіли на питання:
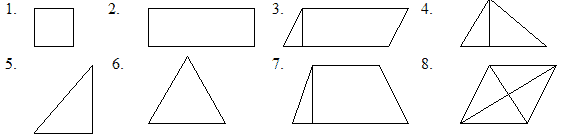
1. Назвіть фігуру, зображену на малюнку. Знайдіть площу кожної фігури для приведених значень. Які формули для знаходження площі ви використовували?
| 1. a) a= 1.2 cm | 2. а=2.5, b=4 | 3. a=8, h=1.25 | 4. a=20, h=15 | 6. a=b=5, c=6 |
| б) S=0.68 m2 | 5. a=4, b=3 | 7. a=20, b=4, h=5 | 8. d1=16, d2=12 |
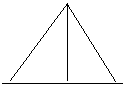
2. Знайдіть висоту трикутника по відомій боковій стороні і прилеглому куту.
3. Звільнення від тяжіння Безіменного острова.
(Пояснення нової теми. Робота у дошки.)
Подорож наших сміливців тривала недовго. На їх дорозі зустрівся Безіменний острів, що володіє властивістю притягувати кораблі. Для подолання його тяжіння необхідно знайти площі трикутника і паралелограма по двох суміжних сторонах і куті між ними.
Двох сміливців поодинці від команди) виходять і виводять формули: S=absin?/2, S=absin?.
4. Подолання несподіваної перешкоди.
Рівно три дні і три ночі пливли мандрівники, і раптом їх корабель несподівано сів на мілину. Для здолання цієї перешкоди необхідно сказати чарівні слова, а саме пригадати формули для знаходження площ паралелограма і прямокутника через діагоналі і кут між ними. До дошки викликаються два учні від кожної команди. Вони працюють разом з класом, роблять відповідні малюнки і оформляють відповідні записи.
5. Поповнення запасів води та їжі.
Дорога наших відважних мандрівників продовжується. Вони бачать скелястий острів, де можна поповнити запаси їжі та води. Платою є створення алгоритму вирішення задач по знаходженню площ многокутників через їх дві суміжні сторони і куту між ними (через дві діагоналі і куту між ними). Блок схема має бути правильно складена кожним членом команди.
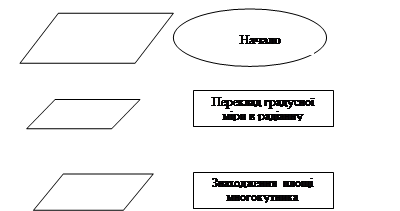

Збирання блок схеми по елементах.
6. Міражі. (Встановлення істинності або помилковості висловів )
Очі закриті. Вислів вірний - руки вперед, помилково - вгору.
Чи Вірно, що:
· Площа прямокутного трикутника дорівнює добутку його катетів?
· ромб – це паралелограм, у якого сторони рівні?
· Площа квадрата дорівнює добутку його суміжних сторін?
· Площа трапеції дорівнює сумі підстав на висоту?
· площа ромба дорівнює добутку двох сторін на синус кута між ними?
· Площа прямокутника дорівнює сумі всіх його сторін?
· Площа трикутника дорівнює половині добутку його основи на висоту?
В результаті злагоджених дій команд, міражі зникли, і з'явився острів Площ.
7. Пошук ключа. (Складання програми і реалізація її на комп'ютері).
Вибір завдань здійснюється учнем із запропонованого списку.
8. Повернення додому. (Підведення підсумків).
Для повернення додому відважним мандрівникам необхідно відповісти на наступні питання:
«Відповівши правильно на поставлені питання, ви взнаєте прізвище швейцарського ученого, який в 1968 році розробив першу версію мови програмування Паскаль.» (Ніклаус Вірт).
1. Автор безсмертного твору «Початків», виданого більше 2000 років тому, такого, що жив в III столітті до нашої ери. (Евклід).
2. Найбільший математик Сіракуз (287 –212г.г.). (Архімед).
3. Старогрецький математик, що жив в 3 столітті до н. ери. Його ім'ям названа формула для знаходження площі трикутника. (Герон).
4. Його ім'ям називають клятву, яку дають лікарі. Він досліджував площі плоских фігур, обмежених прямими лініями і дугами. (Гіппократ).

Підсумки підводяться в командній першості і в особистому заліку.
Завдання до етапу “Пошук ключа..”
Виберіть задачу для вирішення. Напишіть програму для вирішення задачі і виконаєте її при вказаних значеннях змінних.
Похожие работы
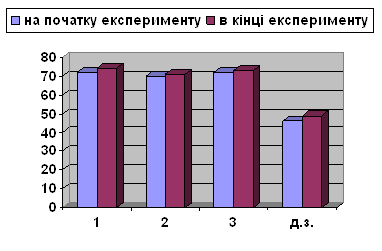
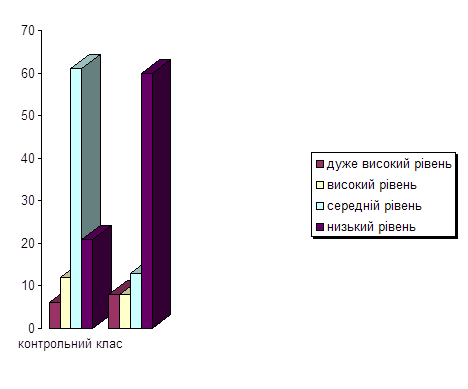
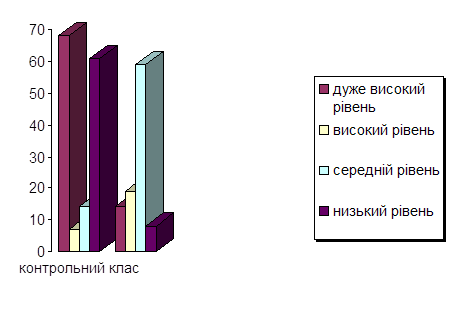
... 2 А клас (експериментальний клас) Правильно виконали (у %) № завдання Діаграма 2. 2 Б клас (контрольний клас) Правильно виконали (у %) № завдання Аналізуючи одержані результати експериментального дослідження можна зробити висновок, що дидактична гра – це ефективний метод навчання математики молодших школярів. Ігри та ігрові ситуації допомагають учням у навчанні, органі ...
... активності, позитивного ставлення до навчання». Як свідчать дослідження, не можна вирішувати успішно питання навчання без організації оволодіння учнями уміннями мислити. Евристична бесіда як метод розвитку пізнавальної активності нараховує вже кілька тисячоліть, вперше він увійшов в ужиток як “сократична бесіда”, він імені славетного філософа Сократа, що вів філософські з учнями бесіди, що мали ...
орчих ігор. Завдання курсової роботи: 1. Науково осмислити можливості використання ігор у вихованні молодших школярів. 2. Підготувати методичні рекомендації для вихователів із впровадження у навчально-виховний процес творчих ігор. Цими питаннями у своїх працях займалися такі відомі педагоги як: Бондаренко А.К. "Дитячі ігри" , Усова А.П. "Роль игры в воспитании детей", Ельконин Д.В. "Психологія ...
... дсумкова, контрольно-перевірна) і за рівнем пізнавальної самостійності учнів (репродуктивна і евристична). 5. Вивчення стану використання бесіди на уроках курсу "Я і Україна" в початковій школі засвідчило необхідність удосконалення процесу організації діалогічного методу навчання. 6. Визначено педагогічні умови організації бесіди на уроках курсу "Я і Україна": — При підготовці до уроку вчитель ...


0 комментариев