Линии задержки на фазовых звеньях

2.         Линии задержки на фазовых звеньях

 

У этого типа ЛЗ полностью снимается проблема АЧХ. Действительно, ОПФ фазового звена имеет вид

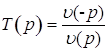
Следовательно,

 

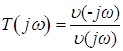
Решая задачу синтеза ЛЗ на фазовых звеньях, необходимо найти такой полином Гурвица , у которого в заданном интервале частот функция  аппроксимировала бы линейную зависимость .

Интервал аппроксимации чаще всего ограничивается полосой частот , что характерно для ЛЗ видеосигналов.

Для того чтобы решение было общим для любых конкретных значений  аппроксимируемой функции  удобно от переменной  перейти к нормированной частот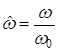е , где  – нормирующая частота, и нормированному времени  

При этом аппроксимируемая функция переходит в функцию , а интервал аппроксимации – в интервал 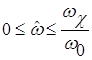. Обозначим . Тогда , а аппроксимирующая функция будет иметь вид:

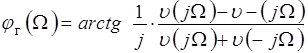
В свою очередь, учитывая свойства реактансных функций последнее выражение можно записать в виде

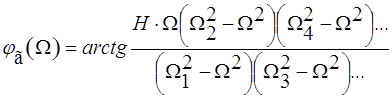
где ,

Н – некоторая функция.

а) Интерполирование линейной фазы

Для приближенного воспроизведения заданной линейной зависимости  можно применять интерполирование, расположив узлы интерполяции в n равностоящих точках 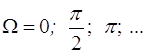. Такие же значения будут принимать в этих точках аппроксимируемая  и аппроксимирующая функции. Для получения указанных значений под знаком  должны чередоваться ноль и полюс, то есть числитель и знаменатель должны поочередно обращаться в ноль.

В таком случае, например, при четырех узлах интерполирования 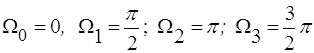 и Н > 0, аппроксимирующая функция будет иметь вид

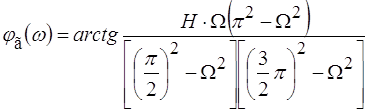
Значение Н можно найти, если потребовать, чтобы в точке  производная функции  совпадала бы со значением производной . В рассматриваемом примере , а при малых

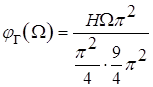 , то .

Приравняв это значение к единице, получим:

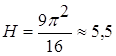
График полученной функции

 

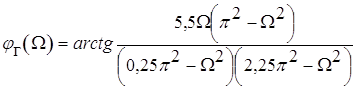
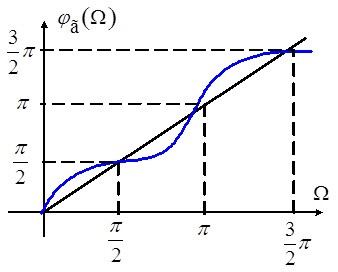
Рисунок 5

Числитель найденной функции  представляет собой нечетную, а знаменатель – четную части комплекса полинома Гурвица. Поэтому

Собственно же полином Гурвица от нормированного переменного  имеет вид

б) Линии задержки с равноволновыми частотными характеристиками

Из рисунка 5 нетрудно заметить, что отклонения аппроксимируемой функции и аппроксимирующей функции между узлами неодинаково. Поэтому найденное методом интерполирования решение, хотя и удовлетворительно воспроизводит заданную зависимость, следует рассматривать как первое приближение, которое затем можно уточнить.

Трифоновым И.И. с помощью ЭВМ была найдена совокупность полиномов Гурвица различных степеней n, у которых функция  аппроксимирует линейную зависимость  с минимальной в смысле Чебышева погрешностью. Например, полином четвертой степени имеет вид

График разности  показан на рисунке 6.

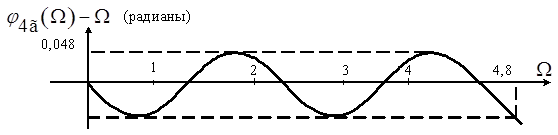
Рисунок 6

в) Линии задержки с монотонными частотными характеристиками.

Другим способом аппроксимации фазы является аппроксимация по Тейлору. В этом случае функции  для точки  находятся аналитически и включают в себя так называемые полиномы Бесселя, как разновидность полиномов Гурвица

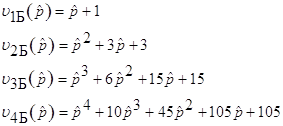
и т. д. (см. справочную литературу).

Полиному Бесселя  степени n соответствует функция , которая в точке  разлагается в ряд

,

где  есть коэффициенты ряда, которые выражаются через функции Бесселя, чем и обусловлено название рассматриваемых полиномов.

На рисунке 7 приведены графики  для нескольких полиномов Бесселя младших степеней, а на рисунке 8 графики , аппроксимирующие постоянное групповое время

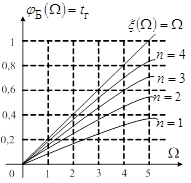
Рисунок 7

Рисунок 8

Из рисунка 8 видно, что частотные зависимости группового времени прохождения ЛЗ являются максимально плоскими. Из него также видно, что интервал аппроксимации увеличивается с ростом степени полинома, а погрешность приближения монотонно возрастает с ростом

3. Линии задержки на фильтрах нижних частот

В подавляющем большинстве случаев для ЛЗ этого типа используется ФНЧ с фазочастотными характеристиками, близкими к линейной зависимости. ОПФ такой ЛЗ имеет такой же вид, как и у обычного полиномиального ФНЧ:

Рабочая фаза и функция группового времени задержки будут выражаться зависимостями:

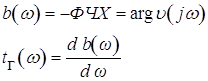
В качестве полиномов  на практике могут быть использованы разновидности полиномов Гурвица, например, Бесселя, Трифонова и др.

Если  – полином Бесселя, то характеристика имеет максимально плоский вид (рис. 8).

Схемы пассивной реализации такой ЛЗ имеют лестничную структуру, в которой в продольных ветвях стоят индуктивные элементы, в поперечных – емкостные, а в общее число реактивных элементов равно n.

Полиномы Трифонова обеспечивают наилучшее в смысле чебышевского критерия близости воспроизведение линейной ФЧХ в рабочем диапазоне частот. Естественно, что функция  при этом равноволновый характер не сохраняет.

Наибольшее практическое распространение получили ЛЗ, построенные на полиномиальных ФНЧ бесселевского типа. Основным недостатком, сдерживающим их широкое применение, является достаточно заметная неравномерность характеристики затухания Δа в рабочей полосе частот.

Заключение

 

В данной работе рассмотрены направления синтеза пассивных линий задержки в LC базисе. При их проектировании следует использовать справочную литературу, например: Авраменко В.Л., Ланнэ А.А. «Электрические линии задержки и фазовозвращатели» – ВАС, 1969 г.;

В случае реализации ЛЗ в ARC – базисе могут быть применимы любые из известных методов расчета со всеми присущими им особенностями. В качестве общего недостатка активной реализации следует отметить чрезмерную избыточность в схеме активных приборов.

Литература

 

1. Белецкий А.Ф. «Теория линейных электрических цепей » Москва 1986 - с. 513- 518.

2.  Белецкий А.Ф. « Линейные устройства аппаратуры связи. Конспект лекций»

3. Бакалов В.П. «Теория электрических цепей» Москва «Радио и связь» 1998 с. 404-411