Навигация
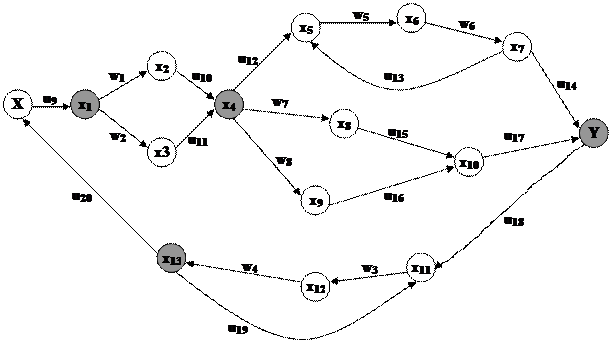
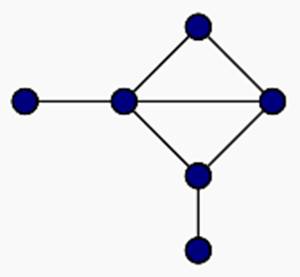
Построение сигнального графа
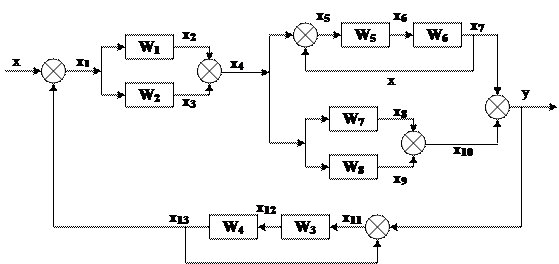
2. Построение сигнального графа.
Перепишем уравнения в общем, виде для построения графа системы:
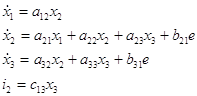
Построение графа произведем в два шага:
Шаг 1. Ставим точки входа, выхода системы ![]() и векторы параметров
и векторы параметров
Шаг 2. Соединяем все параметры связями согласно системе уравнений.
|
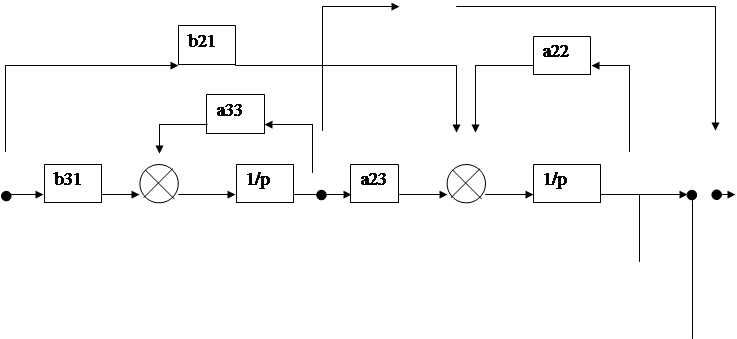
![]()
![]() e X 3 X 3 X 2 X 2 i2
e X 3 X 3 X 2 X 2 i2
| |||||
X 1 X 1
3) Нахождение передаточной функции по формуле Мейсона.
k-количество возможных путей от входа к выходу
![]() -определитель графа
-определитель графа
Pk-коэффициент передачи k пути от входа к выходу
![]() -определитель всех касающихся контуров при удалении k-ого пути
-определитель всех касающихся контуров при удалении k-ого пути
![]() =1-(сумма коэффициентов передачи всех отдельных контуров)+(сумма всевозможных произведений из двух некасающихся контуров) - (сумма всевозможных комбинаций из трех некасающихся контуров)+…+…
=1-(сумма коэффициентов передачи всех отдельных контуров)+(сумма всевозможных произведений из двух некасающихся контуров) - (сумма всевозможных комбинаций из трех некасающихся контуров)+…+…
Последовательность нахождения w(p) по формуле Мейсона:
1) В данном случае есть 1 путь от входа к выходу:
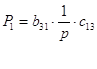
2) В системе имеется 4 замкнутых контуров:
![]()
![]()
![]()
![]()
3) Определитель системы включает 4 контура и 2 пары некасающихся контуров L1,L2; L1,L4
![]()
4) Количество сомножителей равно количеству прямых путей. Выражение для ![]() записывается как выражение для
записывается как выражение для ![]() , но разрываются контуры, через которые проходит прямой путь Pi.
, но разрываются контуры, через которые проходит прямой путь Pi.
Сомножитель ![]() для первого пути. При размыкании первого пути 2 контура размыкаются, кроме L2,L4
для первого пути. При размыкании первого пути 2 контура размыкаются, кроме L2,L4
![]()
5) Запишем и преобразуем выражение передаточной функции:
![]()
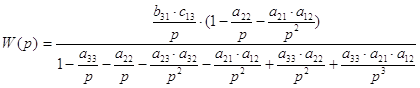
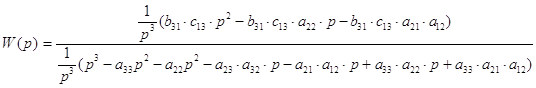
![]()
![]()
![]()
![]()
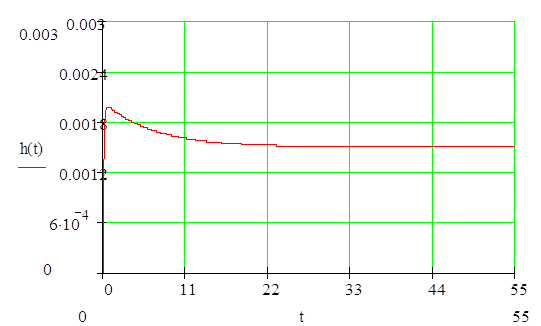
Найдем переходную функцию и построим ее график:
 |
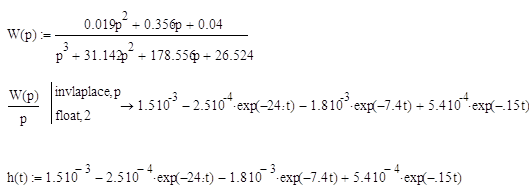 |
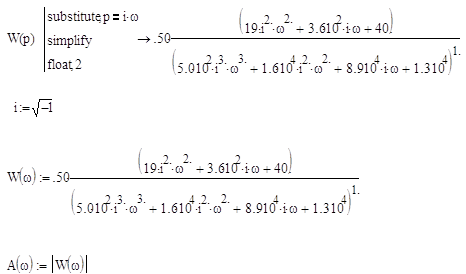 |
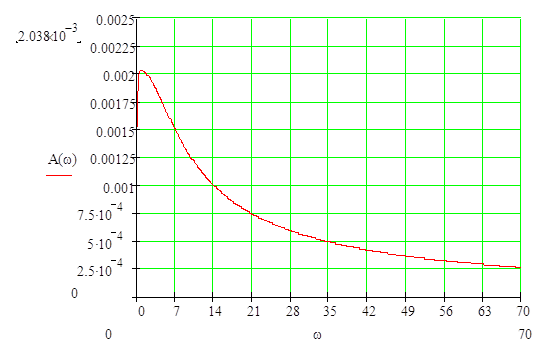
Найдем амплитудно-частотную характеристику (АЧХ):
 |
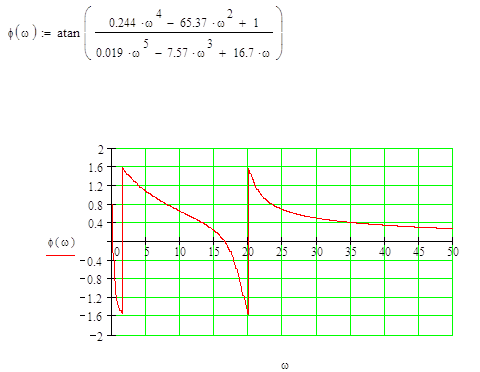
Найдем фаза частотную характеристику (ФЧХ):
 |
Определим оценки качества системы: прямые и косвенные.
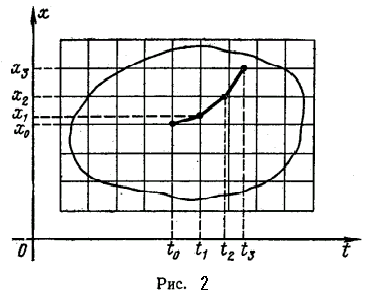
Прямые оценки определяются графически по графику переходного процесса.
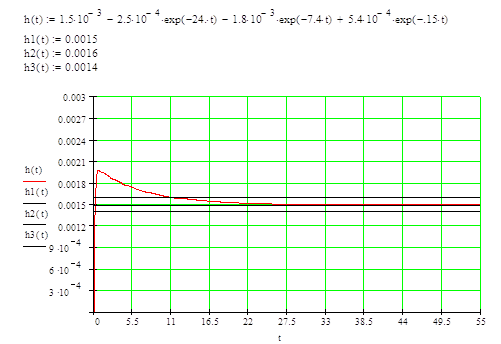 |
Время переходного процесса: tn=11
Перерегулирование:
![]()
Колебательность: п=0,5
Время нарастания регулируемой величины: t=0,385
Время первого согласования: tm=0,66
Косвенные оценки качества системы определяются по графику АЧХ.
Колебательность:
![]()
Резонансная частота: wp=0,83
Частота среза: wсp=10
![]()
Полоса пропускания частот: ![]()
II-часть
Задание1: По заданной корреляционной функции Kx(t) определить спектральную плотность Sx(w) для белого шума, который подается на вход формирующего фильтра.
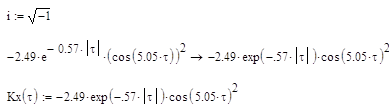 |
По данной корреляционной функции определим спектральную плотность:
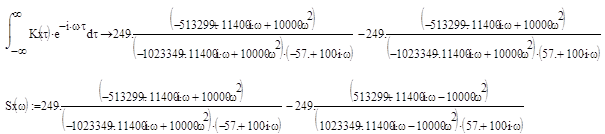 |
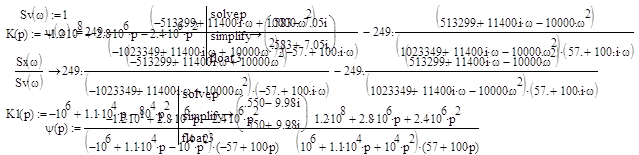 |
Найдем корни характеристических уравнений передаточной функции фильтра:
Изобразим эти корни на комплекснрй плоскости:
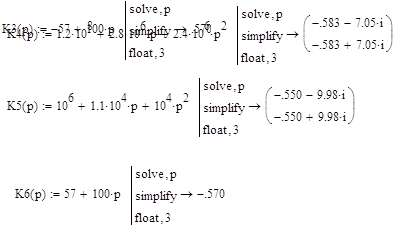 |
Система будет устойчивой, если корни характеристического уравнения лежат во 2-ом квадранте, следовательно, условию устойчивости системы соответствуют корни:
P7= -0,583+7,05i
P9= - 0,550+9,98i
P10= -0,570
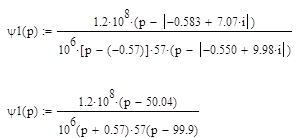 |
Из этого следует, что передаточная функция фильтра будет иметь
следующий вид:
С учетом фильтра наша схема будет иметь следующий вид:
![]()
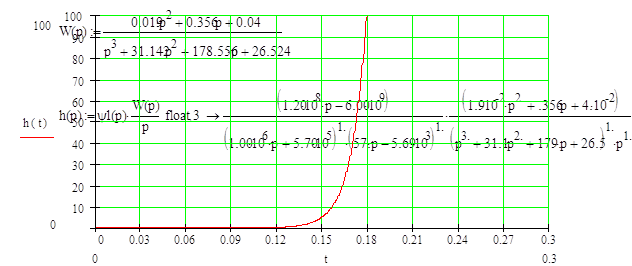
Найдем переходную функцию данной системы, построим ее график и определим прямые оценки качества системы.
Вывод: По графику видно, что фильтр вносит в систему изменения, приводящие к неустойчивости системы. Вследствие чего оценки качества системы определить нельзя.
Похожие работы
... D=1- W3W4(W1W5W6+ W7+ W1W8+ W2W6 W7+ W2W7+2W2W8+ 1)+ W5W6(W3W4(W7+ W1W5W6+ W2W7+ W2W8+1)-1) Для x1 Для x4 Для y Для х13 Задание 2. Синтез комбинационных схем. 2.1 Определение поставленной задачи Устройство, работа которого может быть представлена на языке алгебры высказываний, принято называть логическим. Пусть такое устройство имеет n ...
... противоположные подходы, но нельзя считать ни один из них "юридически законным" или вытекающим из каких ни будь законов природы, нельзя считать стиль управления системой на основе системного анализа "правильным", "современным", "куль-турным". Другое дело — не знать о возможности применения системного подхода к вопросам управления — вот это неправильно, некультурно. Пример системного подхода ...
... в момент t, образует пространство выхода системы. Множество всех значений, которые может принять вектор состояния x в момент t, образует пространство состояний системы. 3.3. Описание непрерывных систем с помощью системы дифференциальных уравнений В любой момент времени t состояние системы является функцией начального состояния x(t0) и вектора входа m(t0, t), то есть x(t)=F[x(t0); m(t0; t)], ...
... Рассела и во многом базируется на работе Бертрана Рассела и Альфреда Уайтхэда «Principia Mathematica» (этот фундаметальный трёхтомник математической логики до сих пор не издан на русском языке)[8]. Заключение Прародителем информатики является кибернетика, основанная американским математиком Норбертом Винером, опубликовавшим в 1948 году одноименную книгу. Основоположником ...
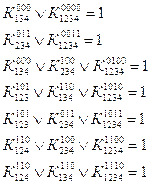
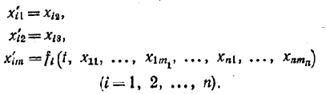

0 комментариев