Навигация
Обработка многократных измерений
Введение
Измерения — один из важнейших путей познания природы человеком. Они играют огромную роль в современном обществе. Наука и промышленность не могут существовать без измерений. Практически нет ни одной сферы деятельности человека, где бы интенсивно не использовались результаты измерений, испытаний и контроля.
Диапазон измерительных величин и их количество постоянно растут и поэтому возрастает и сложность измерений. Они перестают быть одноактным действием и превращаются в сложную процедуру подготовки и проведения измерительного эксперимента и обработки полученной информации.
Другой причиной важности измерений является их значимость. Основа любой формы управления, анализа, прогнозирования, контроля или регулирования — достоверная исходная информация, которая может быть получена лишь путем измерения требуемых физических величин, параметров и показателей. Только высокая и гарантированная точность результатов измерений обеспечивает правильность принимаемых решений.
Методической основой стандартизации являются математические методы, включая предпочтительные числа и ряды предпочтительных чисел, параметрические ряды, а также унификация деталей и узлов, агрегатирование, комплексная и опережающая стандартизация.
Предпочтительные числа и ряды предпочтительных чисел необходимы для выбора оптимального ряда параметров и типоразмеров готовых изделий. Набор установленных значений параметров составляет параметрический ряд, который строится по системе предпочтительных чисел.
1. Обработка результатов многократных измерений:
Систематическая погрешность (0,25)%
Доверительная вероятность 0,1%
Результаты измерений: 99,72; 100,71; 91,55; 96,02; 97,68; 93,04; 92,84; 93,14; 97,31; 94,7; 90,24; 92,15; 96,02; 100,13; 94,51; 94,6; 93,01; 97,47; 96,54; 94,96; 96,29; 99,63; 94,16.
Обработка многократных измеренийПредполагаем, что измерения равноточные, т.е. выполняются одним экспериментатором, в одинаковых условиях, одним прибором. Методика сводится к следующему: проводят n наблюдений (единичных измерений) и фиксируют n результатов измерений одного и того же значения физической величины.
1) Исключаем известные систематические погрешности результатов измерений и получаем исправленный результат ![]() ;
;
![]() =
= ![]() ×(1- Σ/100),
×(1- Σ/100),
где Σ=0,25 % - систематическая погрешность.
![]() =
= ![]() ×(1-0.25/100)
×(1-0.25/100)
![]() =
=![]() × 0.9975
× 0.9975
![]() = 99,74 × 0.9975;
= 99,74 × 0.9975; ![]() = 99,4707
= 99,4707
![]() =100,71 × 0.9975;
=100,71 × 0.9975; ![]() =100,4582
=100,4582
![]() =91,55 × 0.9975;
=91,55 × 0.9975; ![]() =91,32113
=91,32113
![]() =96,02 × 0.9975;
=96,02 × 0.9975; ![]() =95,77995
=95,77995
![]() =97,68 × 0.9975;
=97,68 × 0.9975; ![]() =97,4358
=97,4358
![]() =93,04 × 0.9975;
=93,04 × 0.9975; ![]() =92,8074
=92,8074
![]() =92,84 × 0.9975;
=92,84 × 0.9975; ![]() =92,6079
=92,6079
![]() =93,14 × 0.9975;
=93,14 × 0.9975; ![]() =92,90715
=92,90715
![]() =97,31 × 0.9975;
=97,31 × 0.9975; ![]() =97,06673
=97,06673
![]() =94,7 × 0.9975;
=94,7 × 0.9975; ![]() =94,46325
=94,46325
![]() =90,24 × 0.9975;
=90,24 × 0.9975; ![]() =90,0144
=90,0144
![]() =92,15 × 0.9975;
=92,15 × 0.9975; ![]() =91,91963
=91,91963
![]() =96,02 × 0.9975;
=96,02 × 0.9975; ![]() =95,77995
=95,77995
![]() =100,13 × 0.9975;
=100,13 × 0.9975; ![]() =99,87968
=99,87968
![]() =94,51 × 0.9975;
=94,51 × 0.9975; ![]() =94,27373
=94,27373
![]() =94,6 × 0.9975;
=94,6 × 0.9975; ![]() =94,3635
=94,3635
![]() =93,01 × 0.9975;
=93,01 × 0.9975; ![]() =92,77748
=92,77748
![]() =97,47 × 0.9975;
=97,47 × 0.9975; ![]() =97,22633
=97,22633
![]() =96,54 × 0.9975;
=96,54 × 0.9975; ![]() =96,29865
=96,29865
![]() =94,96 × 0.9975;
=94,96 × 0.9975; ![]() =94,7226
=94,7226
![]() =96, 29 × 0.9975;
=96, 29 × 0.9975; ![]() =96,04928
=96,04928
![]() =99, 63 × 0.9975;
=99, 63 × 0.9975; ![]() =99,38093
=99,38093
![]() =94, 16 × 0.9975;
=94, 16 × 0.9975; ![]() =93,9246
=93,9246
![]() =2190,928
=2190,928
2) Находим среднее арифметическое значение исправленных результатов и принимают его за результат измерений
![]() ;
;
n=23
![]() =
=![]() ×2190,928
×2190,928
![]() =95,2577
=95,2577
3) Вычисляем оценку среднеквадратического отклонения результата измереий.
а) находим отклонения от среднего арифметического ![]() ;
;
![]() = 95,2577-99,4707
= 95,2577-99,4707 ![]() =-4,213
=-4,213
![]() =95,2577-100,4582
=95,2577-100,4582 ![]() =-5,201
=-5,201
![]() =95,2577-91,32113
=95,2577-91,32113 ![]() =3,938
=3,938
![]() =95,2577-95,77995
=95,2577-95,77995 ![]() =-0,522
=-0,522
![]() =95,2577-97,4358
=95,2577-97,4358 ![]() =-2,178
=-2,178
![]() =95,2577-92,8074
=95,2577-92,8074 ![]() =2,450
=2,450
![]() =95,2577-92,6079
=95,2577-92,6079 ![]() =2,650
=2,650
![]() =95,2577-92,90715
=95,2577-92,90715 ![]() =2,351
=2,351
![]() =95,2577-97,06673
=95,2577-97,06673 ![]() =-1,809
=-1,809
![]() =95,2577-94,46325
=95,2577-94,46325 ![]() =0,795
=0,795
![]() =95,2577-90,0144
=95,2577-90,0144 ![]() =5,243
=5,243
![]() 95,2577-91,91963
95,2577-91,91963 ![]() =3,338
=3,338
![]() 95,2577-95,77995
95,2577-95,77995 ![]() =-0,522
=-0,522
![]() =95,2577-99,87968
=95,2577-99,87968 ![]() =-4,622
=-4,622
![]() 95,2577-94,27373
95,2577-94,27373 ![]() =0,984
=0,984
![]() 95,2577-94,3635
95,2577-94,3635 ![]() =0,894
=0,894
![]() =95,2577-92,77748
=95,2577-92,77748 ![]() =2,481
=2,481
![]() =95,2577-97,22633
=95,2577-97,22633 ![]() =-1,968
=-1,968
![]() =95,2577-96,29865
=95,2577-96,29865 ![]() =-1,040
=-1,040
![]() 95,2577-94,7226
95,2577-94,7226 ![]() =0,535
=0,535
![]() 95,2577-96,04928
95,2577-96,04928 ![]() =-0,794
=-0,794
![]() 95,2577-99,38093
95,2577-99,38093 ![]() =-4,123
=-4,123
![]() =95,2577-93,9246
=95,2577-93,9246 ![]() =1,333
=1,333
![]() =0
=0
б) проверили правильность вычислений, и они верны,
т.к. 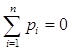 ;
;
в) вычисляем квадраты отклонений от среднего ![]() ;
;
![]() =17,749
=17,749
![]() =27,05
=27,05
![]() =15,507
=15,507
![]() =0,272
=0,272
![]() =4,744
=4,744
![]() =6,003
=6,003
![]() =7,025
=7,025
![]() =5,527
=5,527
![]() =3,72
=3,72
![]() =0,632
=0,632
![]() =27,458
=27,458
![]() =11,142
=11,142
![]() =0,272
=0,272
![]() =21,363
=21,363
![]() =0,968
=0,968
![]() =0,799
=0,799
![]() =6,155
=6,155
![]() =3,873
=3,873
![]() =1,082
=1,082
![]() =0,286
=0,286
![]() =0,630
=0,630
![]() =16,999
=16,999
![]() =1,777
=1,777
![]() =181,033
=181,033
г) определяем оценку среднеквадратического отклонения
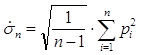 ;
;
![]() =
=![]() ×181,033
×181,033
![]() 0.21×181,033
0.21×181,033
![]() =38,0169
=38,0169
д) находим значение относительной среднеквадратической случайной погрешности
![]() ;
;
![]() =
=![]() =0,399
=0,399
4) Вычисляем оценку среднеквадратического отклонения результата измерения
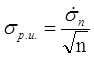 ; n=23
; n=23
![]() =
=![]() =
= ![]() = 7.9268
= 7.9268
5) Вычисляем доверительные границы случайной погрешности результатов измерений:
а) задаются коэффициентом доверия ![]() (доверительной вероятности);
(доверительной вероятности);
α=0.1%
б) по специальным таблицам определяют значение коэффициента Стьюдента (![]() ), соответствующее заданной доверительной вероятности и числу наблюдений;
), соответствующее заданной доверительной вероятности и числу наблюдений;
где, n – число наблюдений;
α – доверительная вероятность
n=23
α=0.1%
t=1.319460
в) находим значение ![]() ;
;
t=1.319460
![]() =7.9268
=7.9268
![]() 1.319460×7.9268
1.319460×7.9268
![]() =10,4591
=10,4591
г) вычисляем доверительные границы ![]() и
и ![]() .
.
![]() =95,2577
=95,2577
![]() =10,4591
=10,4591
95,2577-10,4591=84.7986
95,2577+10,4591=105.7168
6) записываем результат измерений.
84.7986![]() x ≤ 105.7168
x ≤ 105.7168
Похожие работы
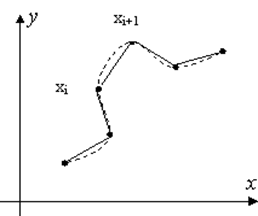
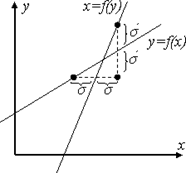
... – оценку дисперсии : (2.3.10) Таким образом мы доказали, что для нормально распределенных данных СКО является лучшей оценкой дисперсии. Обработка результатов совместных измерений При совместных измерениях полученные значения используются для построения зависимостей между измеряемыми величинами. Рассмотрим многофакторный эксперимент, по результатом которого должна быть построена ...
... них не окажется нужной, то тогда средство необходимо разработать вручную, если это оправдано с точки зрения затраченного времени и материальных ресурсов. 2. Обработка геодезических измерений с использованием электронных таблиц Для первоначальной обработки информации, полученной в результате комплекса топографо-геодезических работ, мною использовалась программа “ТОГИ”, являющаяся пакетом ...
... результату измерений из совокупности результатов измерений, выполняемых по одной и той же аттестованной МВИ– приписанные погрешности измерений. 3. Отражающие близость отдельного, экспериментально полученного результата измерений к истинному значению измеряемой величины – статистические оценки характеристик погрешности измерений (статистические оценки погрешности измерений). Нормы погрешности ...
... 4,83·10-4 8 483 4,83·10-7 482 4,82·10-4 9 481 4,81·10-7 481 4,81·10-4 10 480 4,80·10-7 481 4,81·10-4 11 492 4,92·10-7 483 4,83·10-4 12 486 4,86·10-7 495 4,95·10-4 Расчет. 1. Обрабатываем экспериментальные данные по алгоритму, изложенному в п.п. 1–3 задания 2, при этом: – определяем оценки результатов измерений , и ...





0 комментариев