Статистическая обработка экспериментальных данных

Аннотация

Темой курсовой работы является "Статистическая обработка экспериментальных данных". Целью курсовой работы является закрепление изученного материала по дисциплине "Метрология, стандартизация и сертификация" и приобретение практических навыков обработки экспериментальных данных различных видов измерений.

В курсовой работе приведены:

– в разделе "Однократные измерения": порядок выполнения однократного измерения, внесены необходимые поправки и определен предел, в котором находится значение измеряемой величины;

– в разделе "Многократные измерения": результаты измерений, порядок выполнения многократного измерения, исключены ошибки из результатов измерений и определен результат измерений;

– в разделе "Обработка результатов нескольких серий измерений": серии результатов измерений, порядок их обработки и результат измерения;

– в разделе "Косвенные измерения": функциональная зависимость между искомой величиной Z и измеряемыми величинами X и Y, определены и внесены поправки и определен результат измерения;

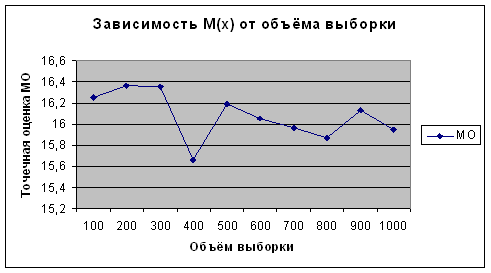
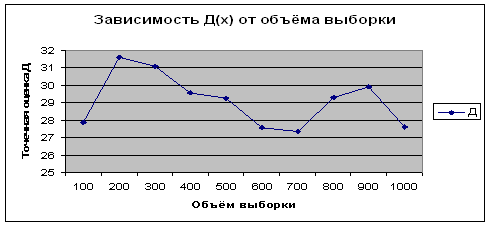
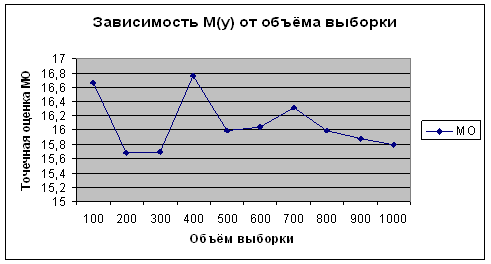
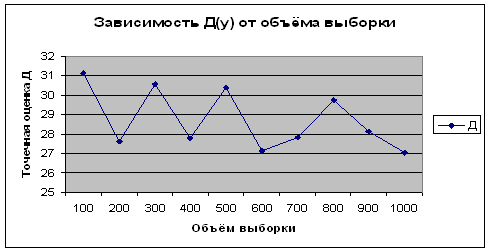
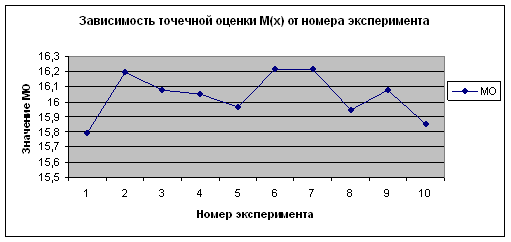
– в разделе "Определение погрешностей результатов измерений методом математической статистики": результаты измерения, выстроены: гистограмма нормального рассеяния измерений и график реального рассеяния измерений в едином масштабе.

Курсовая работа содержит 30 листов расчетно-пояснительной записки.

1

СОДЕРЖАНИЕ

Курсовая работа 1

Введение 3

1. Однократное измерение 4

2. Многократное измерение 6

3. Обработка результатов нескольких серий измерений 13

4. Функциональные преобразования результатов измерений (косвенные измерения) 19

5. Определение погрешностей результатов измерений методом математической статистики 25

29

Литература 30

Введение

Измерения — один из важнейших путей познания природы человеком. Они играют огромную роль в современном обществе. Наука и промышленность не могут существовать без измерений. Практически нет ни одной сферы деятельности человека, где бы интенсивно не использовались результаты измерений, испытаний и контроля.

Диапазон измерительных величин и их количество постоянно растут и поэтому возрастает и сложность измерений. Они перестают быть одноактным действием и превращаются в сложную процедуру подготовки и проведения измерительного эксперимента и обработки полученной информации.

Другой причиной важности измерений является их значимость. Основа любой формы управления, анализа, прогнозирования, контроля или регулирования — достоверная исходная информация, которая может быть получена лишь путем измерения требуемых физических величин, параметров и показателей. Только высокая и гарантированная точность результатов измерений обеспечивает правильность принимаемых решений.

1. Однократное измерение

Условие. При однократном измерении физической величины получено показание средства измерения X = 10. Определить, чему равно значение измеряемой величины, если экспериментатор обладает априорной информацией о средстве измерений и условиях выполнения измерений, согласно исходным данным.

Исходные данные:

Показание средства измерения – X = 10.

Вид закона распределения – равномерный.

Значение оценки среднеквадратического отклонения – S_X= 0,8.

Значение аддитивной поправки – Θ_a = 0,9.

Расчет. Так как в качестве априорной используется информация о законе распределения вероятности, т.е. закон распределения вероятности является равномерным, то пределы, в которых находится значение измеряемой величины, определяются через доверительный интервал:

; (1)

Для равномерного закона распределения вероятности результата измерения значение E (аналог доверительного интервала) можно определить из выражения:

, (2)

где .

Внесем аддитивную поправку и уточним пределы, в которых находится значение измеряемой величины.

2. Многократное измерение

Условие. При многократном измерении одной и той же физической величины получена серия из 24 результатов измерений Q_i; . Определить результат измерения.

Исходные данные:

Таблица 1

№ изме-рения	Результат измерения	№ изме-рения	Результат измерения	№ изме-рения	Результат измерения	№ изме-рения	Результат измерения
1	482	7	483	13	483	19	483
2	485	8	483	14	483	20	482
3	486	9	481	15	483	21	481
4	486	10	480	16	483	22	481
5	483	11	492	17	484	23	483
6	483	12	486	18	484	24	495

Расчет. Порядок расчета и их содержание определяются условием:

10…15 < n< 40…50,

так как n = 24.

1. Определяем оценки результата измерения и среднего квадратического отклонения результата измерения .

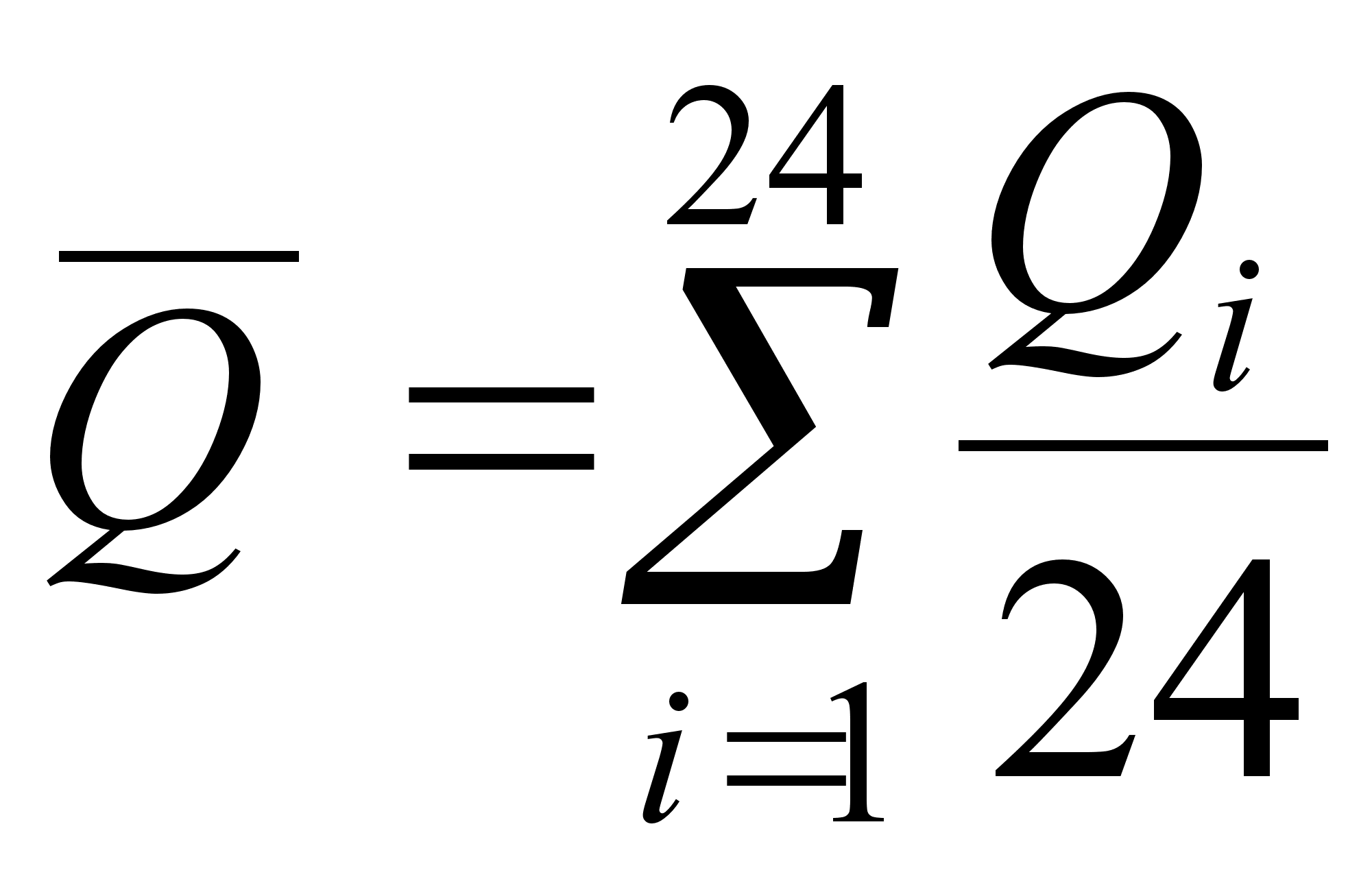
(3)

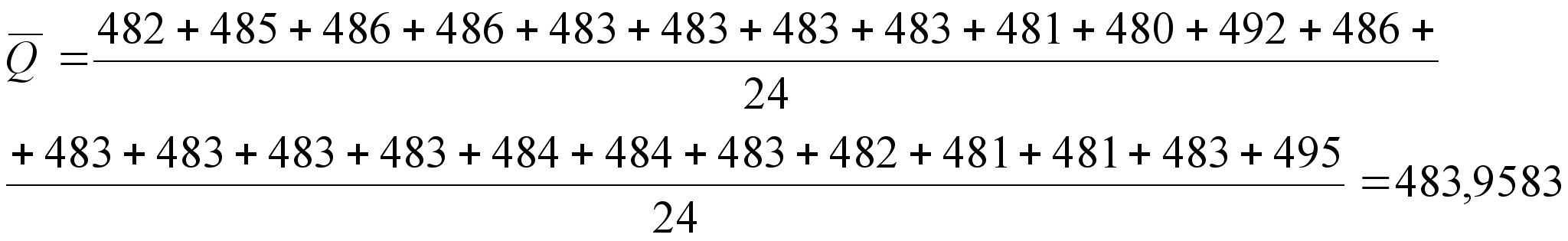
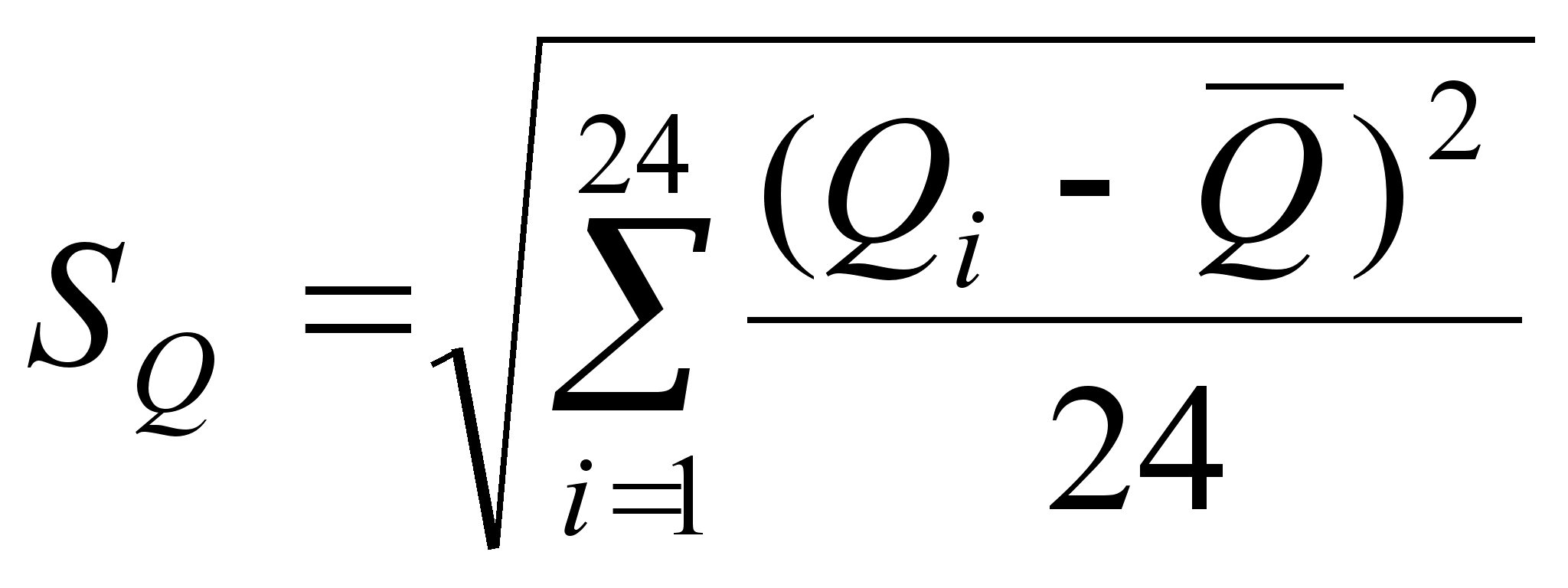(4)

Для удобства вычисления среднего квадратического отклонения результата измерения составим таблицу:

Таблица 2

№ из-мерения	Результат измере-ния (Qi)			№ из-мерения	Результат измере-ния (Qi)
1	482	-1,9583	3,8351	13	483	-0,9583	0,9184
2	485	1,0417	1,0851	14	483	-0,9583	0,9184
3	486	2,0417	4,1684	15	483	-0,9583	0,9184
4	486	2,0417	4,1684	16	483	-0,9583	0,9184
5	483	-0,9583	0,9184	17	484	0,0417	0,0017
6	483	-0,9583	0,9184	18	484	0,0417	0,0017
7	483	-0,9583	0,9184	19	483	-0,9583	0,9184
8	483	-0,9583	0,9184	20	482	-1,9583	3,8351
9	481	-2,9583	8,7517	21	481	-2,9583	8,7517
10	480	-3,9583	15,6684	22	481	-2,9583	8,7517
11	492	8,0417	64,6684	23	483	-0,9583	0,9184
12	486	2,0417	4,1684	24	495	11,0417	121,9184
				Σ		0	258,9583

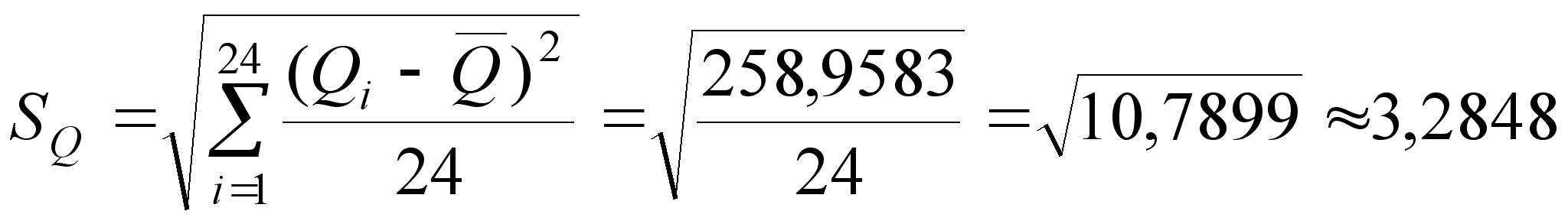
2. Необходимо обнаружить и исключить ошибки. Для этого:

– вычисляем наибольшее по абсолютному значению нормированное отклонение

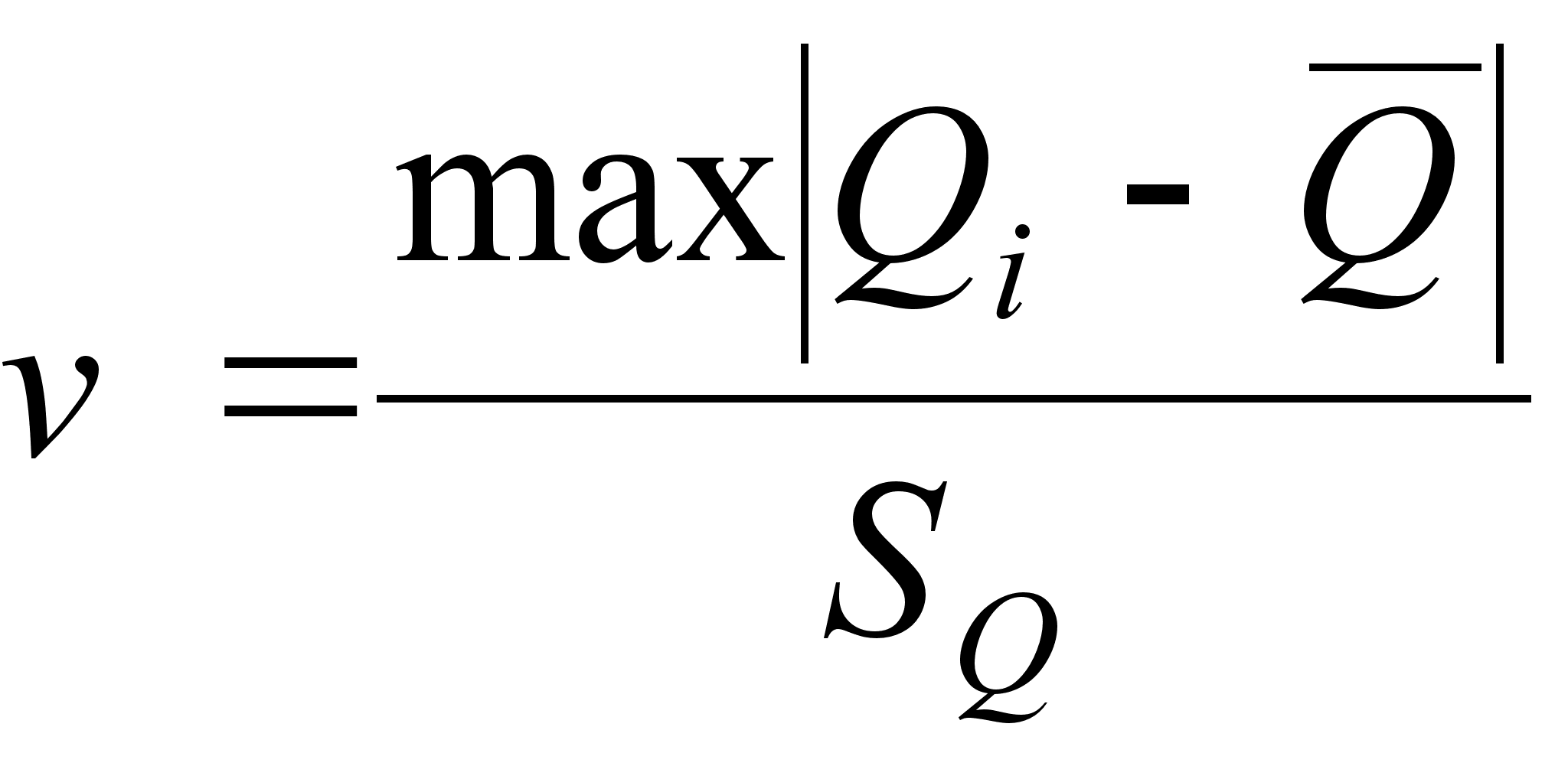(5)

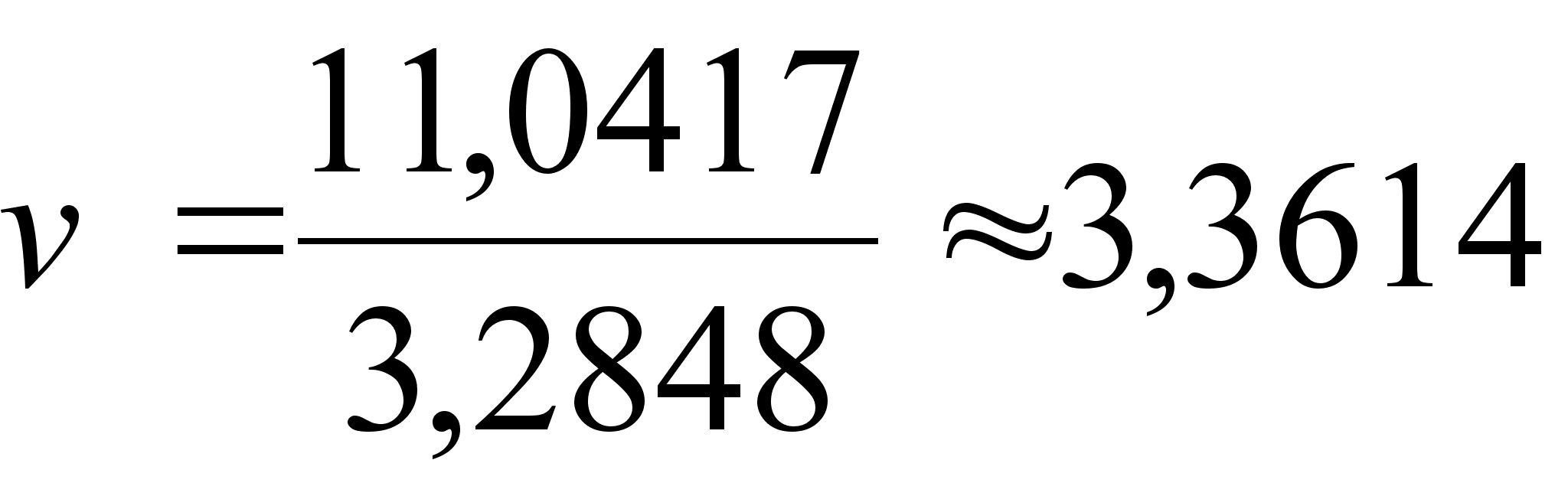
– задаемся доверительной вероятностью P = 0,95 и из соответствующих таблиц (табл. П6) с учетом q = 1 – P находим соответствующее ей теоретическое (табличное) значение :

при n = 24;

– сравниваем с : . Это означает, что данный результат измерения Q_i,т.е. Q₂₄ является ошибочным, он должен быть отброшен. Необходимо повторить вычисления по п.п. 1 и 2 для сокращенной серии результатов измерений и проводить их до тех пор, пока не будет выполняться условие .

Повторяем вычисления, при этом отбрасываем измерение №24:

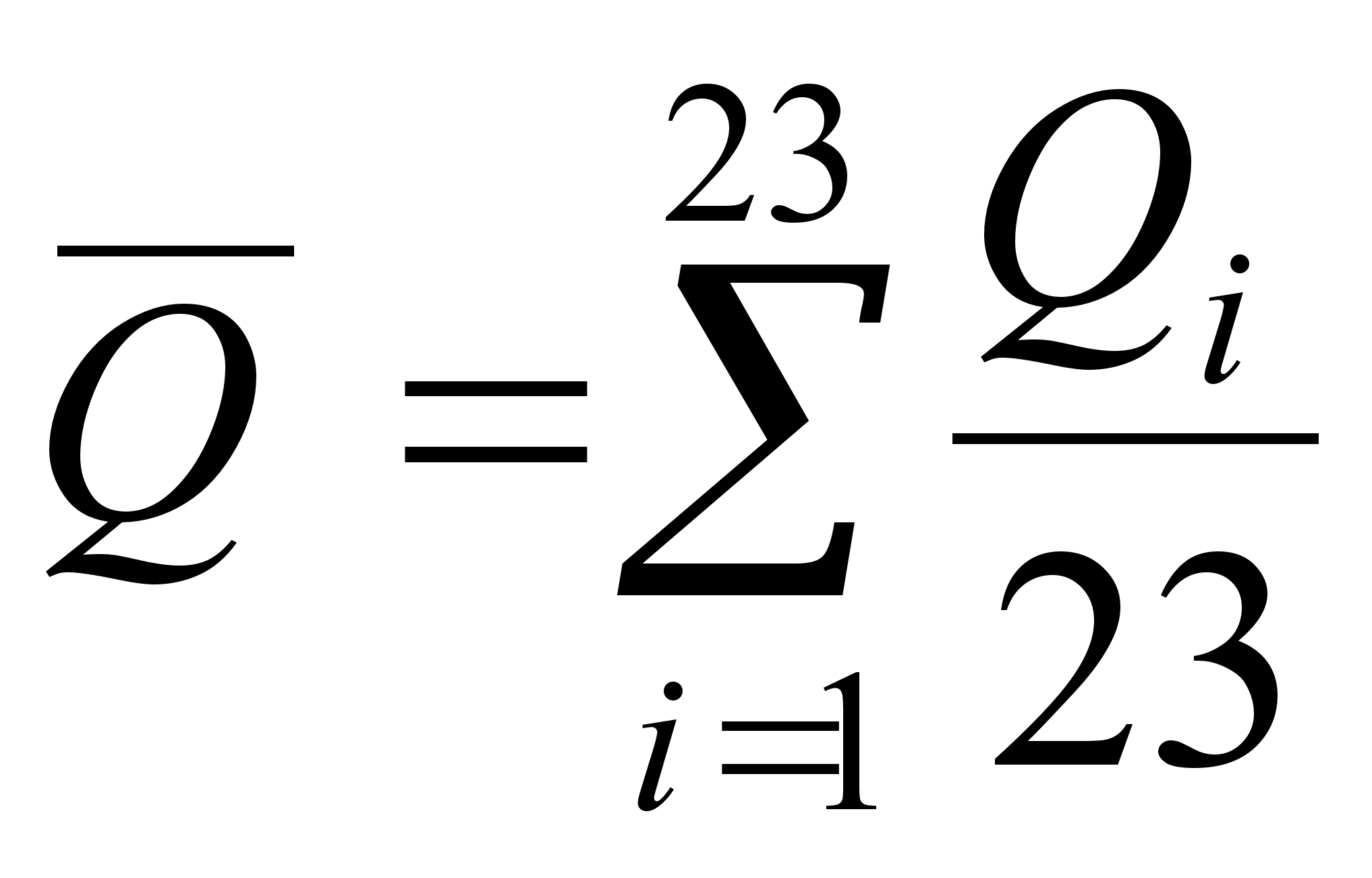
(6)

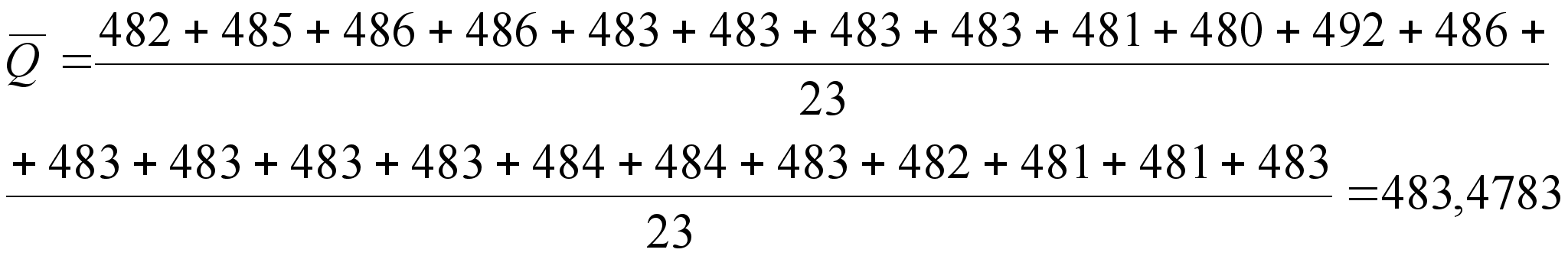
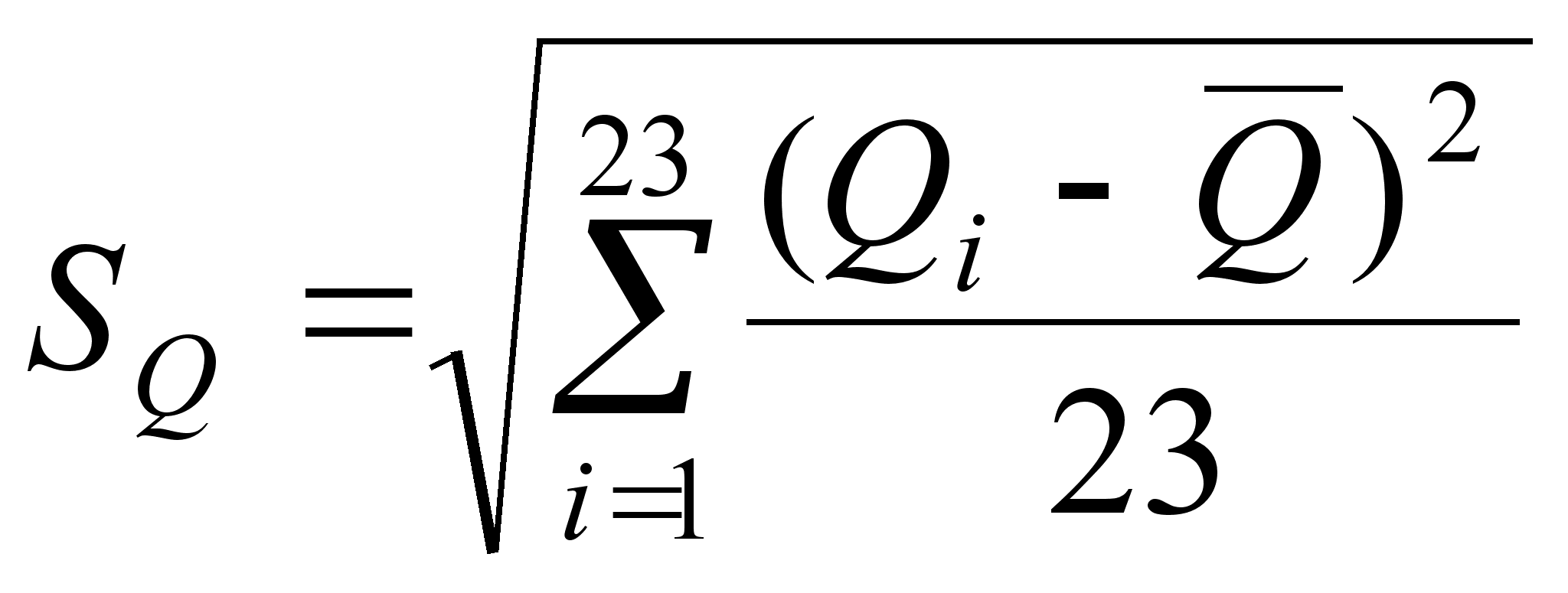(7)

Таблица 3

№ из-мерения	Результат измере-ния (Qi)			№ из-мерения	Результат измере-ния (Qi)
1	482	-1,4783	2,1853	13	483	-0,4783	0,2287
2	485	1,5217	2,3157	14	483	-0,4783	0,2287
3	486	2,5217	6,3592	15	483	-0,4783	0,2287
4	486	2,5217	6,3592	16	483	-0,4783	0,2287
5	483	-0,4783	0,2287	17	484	0,5217	0,2722
6	483	-0,4783	0,2287	18	484	0,5217	0,2722
7	483	-0,4783	0,2287	19	483	-0,4783	0,2287
8	483	-0,4783	0,2287	20	482	-1,4783	2,1853
9	481	-2,4783	6,1418	21	481	-2,4783	6,1418
10	480	-3,4783	12,0983	22	481	-2,4783	6,1418
11	492	8,5217	72,6200	23	483	-0,4783	0,2287
12	486	2,5217	6,3592	Σ		0	131,7391

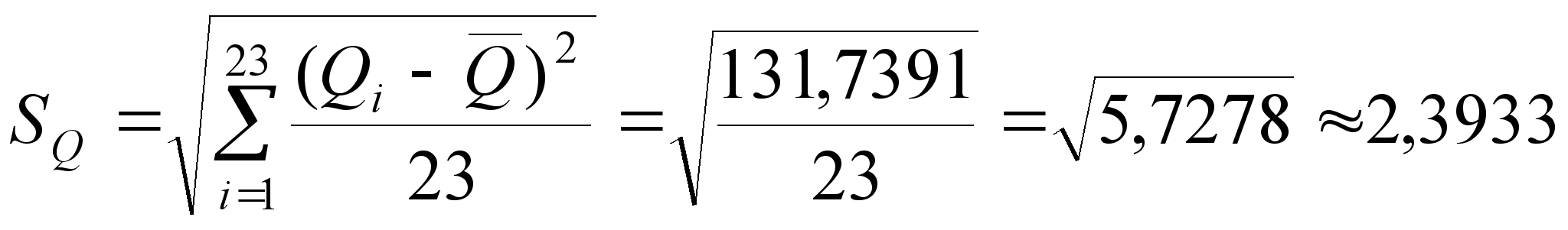
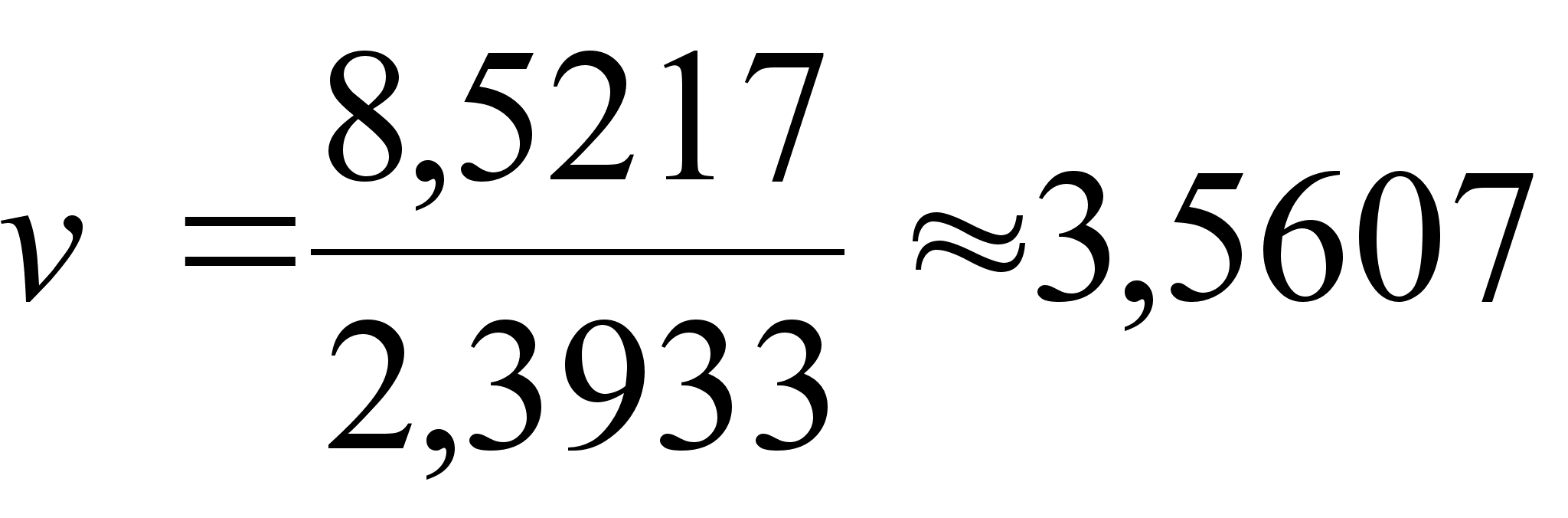
при n = 23;

Сравниваем с : . Отбрасываем измерение №11 и повторяем вычисления.

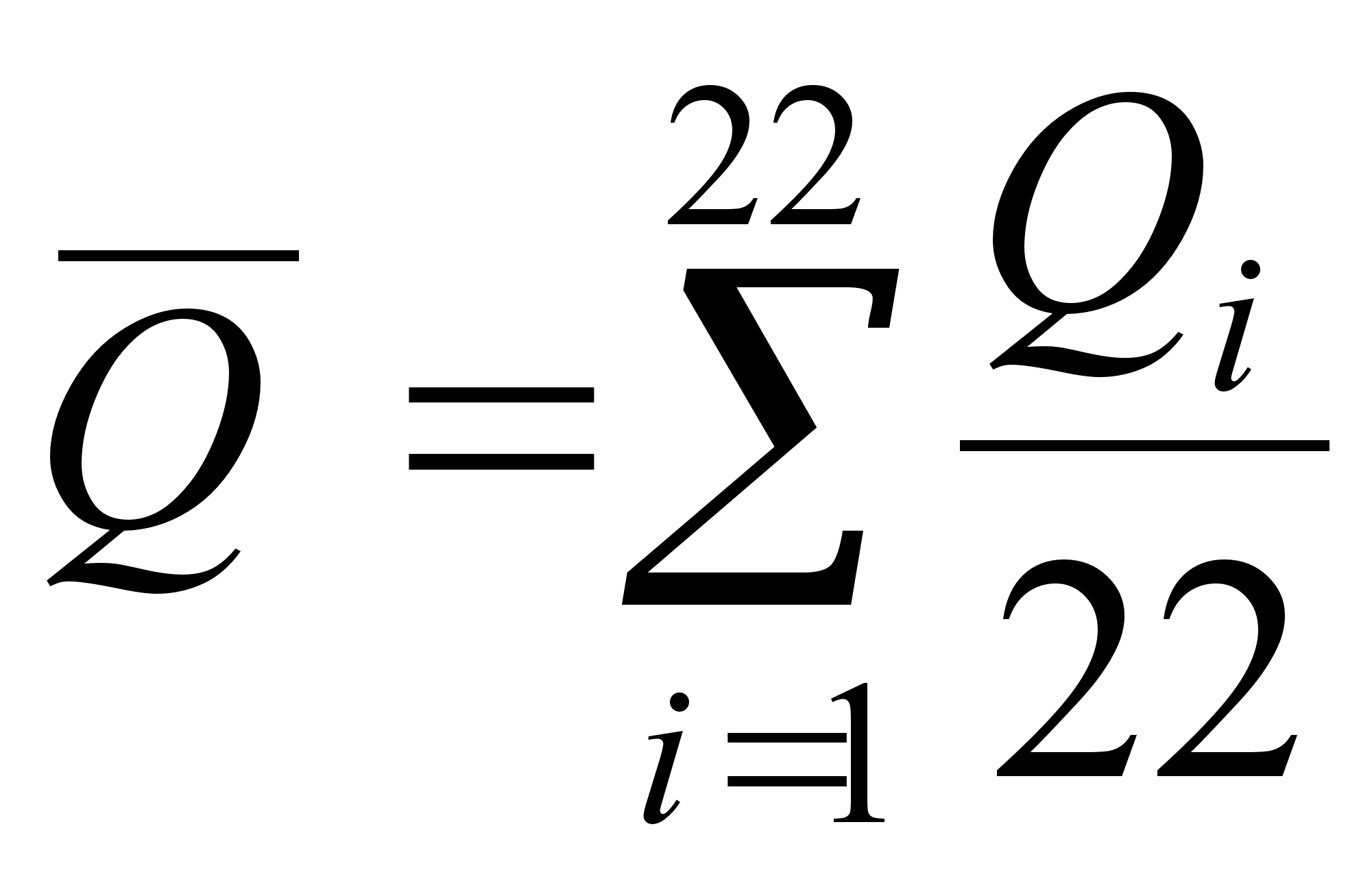
(8)

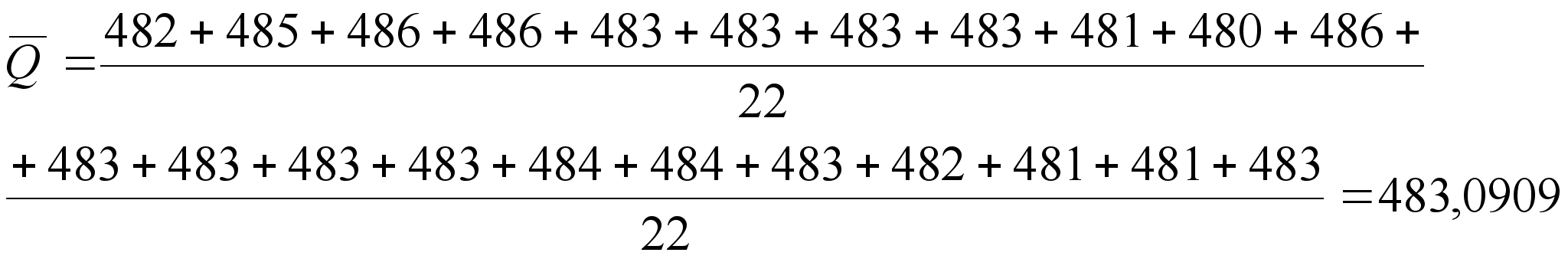
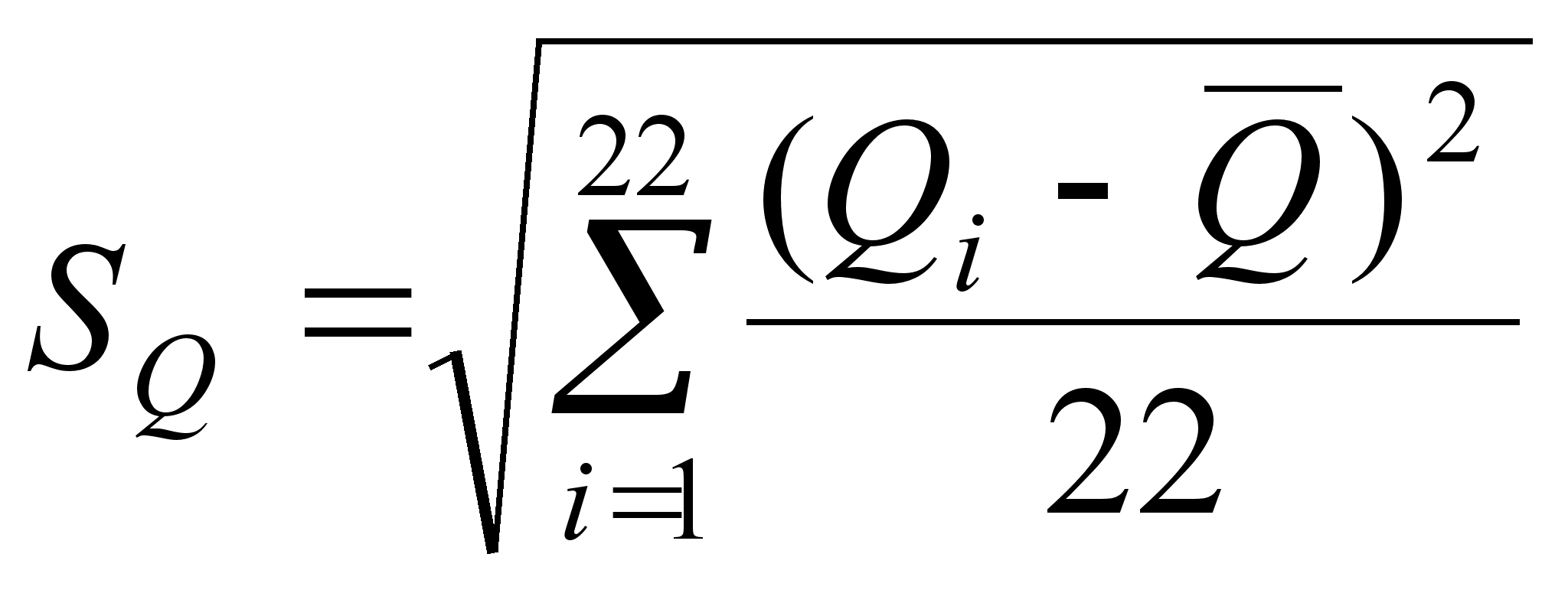(9)

Таблица 4

№ из-мерения	Результат измере-ния (Qi)			№ из-мерения	Результат измере-ния (Qi)
1	482	-1,0909	1,1901	12	483	-0,0909	0,0083
2	485	1,9091	3,6446	13	483	-0,0909	0,0083
3	486	2,9091	8,4628	14	483	-0,0909	0,0083
4	486	2,9091	8,4628	15	483	-0,0909	0,0083
5	483	-0,0909	0,0083	16	484	0,9091	0,8264
6	483	-0,0909	0,0083	17	484	0,9091	0,8264
7	483	-0,0909	0,0083	18	483	-0,0909	0,0083
8	483	-0,0909	0,0083	19	482	-1,0909	1,1901
9	481	-2,0909	4,3719	20	481	-2,0909	4,3719
10	480	-3,0909	9,5537	21	481	-2,0909	4,3719
11	486	2,9091	8,4628	22	483	-0,0909	0,0083
				Σ		0	55,8182

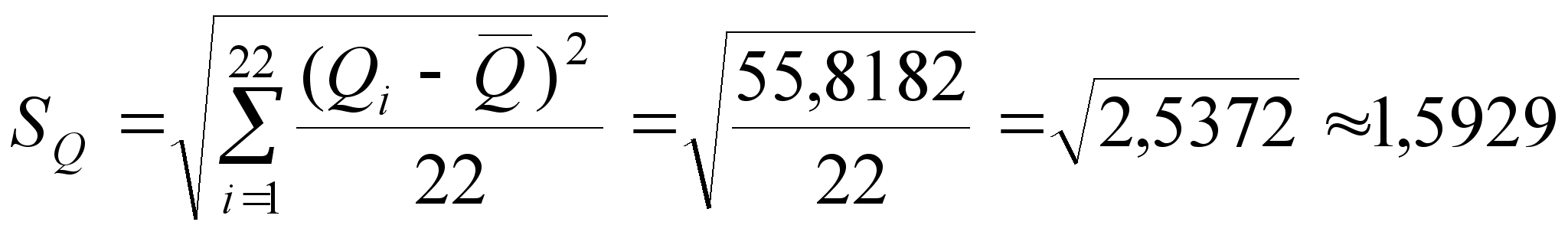
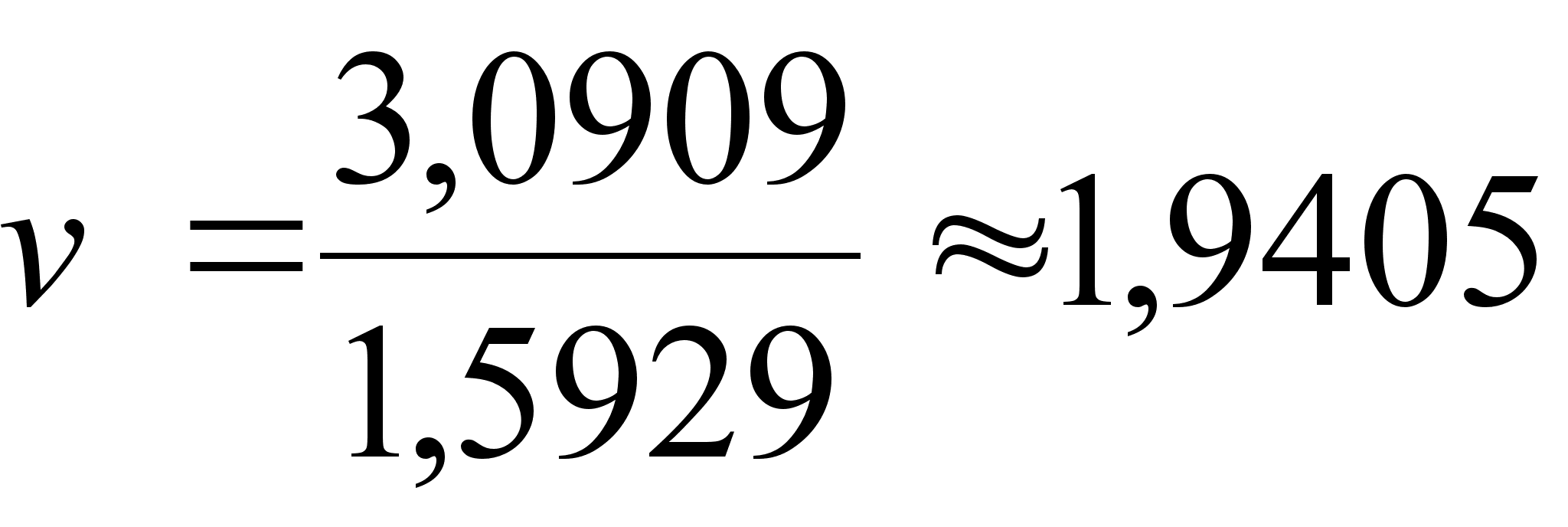
при n = 22;

Сравниваем с . Так как , то результат измерения №10 не является ошибочным и окончательно остается 22 измерения, т.е. n = 22.