Навигация
Элементы статистической термодинамики
23308
знаков
6
таблиц
3
изображения
Элементы статистической термодинамики
1. Распределение Гиббса и распределение Больцмана. Структурные постоянные молекул.
В случае невзаимодействующих частиц идеального газа каноническое распределение Гиббса превращается в распределение Больцмана. В качестве подсистем канонического ансамбля рассматриваются приближённо независимые молекулярные движения:
Поступательное,
Вращательное,
Колебательное,
Электронное,
Ядерное.
Статистические суммы электронного и ядерного состояний равны кратностям вырождения их основных уровней (термов). У электронного движения это число микросостояний, объединённых в терм. У ядерного движения это спиновая мультиплетность ядерного остова.
Таблица 1. Постоянные двухатомных молекул (Табл. 15.2, стр. 467, Даниэльс, Олберти).
| Молекула | NAm - масса приведённая (эксперим), г | R0×1010, м |
| D, эВ | D, кДж/моль |
| Br2 | 39.958 | 2.283 | 323.2 | 1.971 | 190.2219 |
| CH | 0.930024 | 1.1198 | 2861.6 | 3.47 | 334.8909 |
| Cl2 | 17.48942 | 1.988 | 564.9 | 2.475 | 238.863 |
| CO | 6.85841 | 1.1282 | 2170.21 | 11.108 | 1072.037 |
| H2 | 0.504066 | 0.7416 | 4395.24 | 4.476 | 431.9802 |
| H2+ | 0.503928 | 1.06 | 2297 | 2.648 | 255.5594 |
| HCl | 0.979889 | 1.27460 | 2989.74 | 4.430 | 427.5406 |
| HBr | 0.99558 | 1.4138 | 2649.67 | 3.75 | 361.9136 |
| HI | 1.000187 | 1.604 | 2309.53 | 3.056 | 294.9356 |
| KCl | 18.599 | 2.79 | 280 | 4.42 | 426.5757 |
| LiH | 0.881506 | 1.5953 | 1405.649 | 2.5 | 241.2759 |
| Na2 | 11.49822 | 3.078 | 159.23 | 0.73 | 70.45255 |
| NO | 7.46881 | 1.1508 | 1904.03 | 6.487 | 626.0626 |
| O2 | 8.00000 | 1. 20739 | 1780.361 | 5.080 | 490.2726 |
| OH | 0.94838 | 0.9706 | 3735.21 | 4.35 | 419.8198 |
, см-1Таблица 2. Спиновые квантовые числа наиболее распространённых ядер:
| Элемент | Ядро изотопа | Спин ядра I | Мультиплетность ядерного спина 2I+1 |
| Водород | 1H | ½ | 2 |
| Водород | 2D | 1 | 3 |
| Водород | 3T | ½ | 2 |
| Азот | 14N | 1 | 3 |
| Азот | 15N | ½ | 2 |
| Фтор | 19F | ½ | 2 |
| Углерод | 12С | 0 | 1 |
| Углерод | 13С | ½ | 2 |
Похожие работы
... необходимые термодинамические характеристики, а именно: (3.1) Построить явный вид функции свободной энергии для некоторых относительно простых систем можно методом статистической термодинамики. 4. О равновесии. В любом естественно протекающем (самопроизвольном или свободном) процессе свободная энергия системы понижается. При достижении системой состояния термодинамического равновесия её ...
... впервые получены следующие результаты: · Разработана обобщенная координационно-кластерная модель для описания взаимодействий и расчета термодинамических характеристик раствора неметалла в расплаве из трех металлических компонентов. · Установлена связь между термодинамическими свойствами (коэффициентами термодинамической активности и параметрами взаимодействия компонентов первого порядка) и ...
... вызывает процесс. Если процесс заключается в последовательном изменении параметров, приводящих в конечном итоге систему в исходное состояние, то такой процесс называется циклом. Химическая термодинамика, так же как и общая термодинамика, основана главным образом на двух законах (началах). ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ Первое начало термодинамики, окончательно сформулированное Джоулем в ...
... поступательной суммы состояний. ; (3) 1) Вращательная статистическая сумма (на 2 степени свободы) должна быть исправлена с учётом симметрии и неразличимости состояний гомоядерной молекулы при её поворотах на 180o. Эта статистическая сумма сокращается на число симметрии . Для 2-х атомных гомоядерных молекул =2. Для вращения вокруг оси симметрии 3-го порядка =3. Частицы с ...
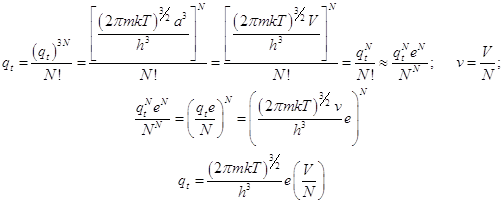
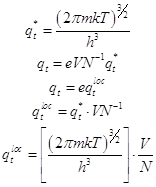
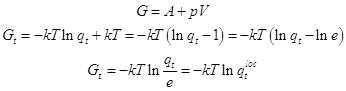
0 комментариев