Навигация
Жесткий ротатор. Уравнение Шредингера
7539
знаков
1
таблица
0
изображений
5. Жесткий ротатор. Уравнение Шредингера.
5.1. Согласно вышеизложенному, уравнение Шредингера для жесткого ротатора может быть представлено так
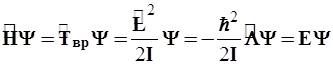(11)
Поскольку момент инерции постоянен (I=const), волновые функция жёсткого ротатора с точностью до постоянного множителя совпадают с собственными функциями оператора Лежандра. Последние обозначаются символом 
и носят название шаровых, или сферических функций. Это значит, что должно быть справедливым операторное уравнение, следующее из (11)
(12)
где 
– собственное значение оператора Лежандра, связанное с квадратом момента импульса и энергией вращения;
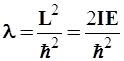(13)
5.2. Поэтому следующий этап решения нашей задачи состоит в нахождении собственных функций операторного уравнения (4.57), которое в развёрнутом виде представляется так
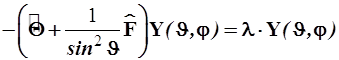(14)
Конструкция уравнения (14), включающего сумму операторов, каждый из которых содержит одну переменную, позволяет легко произвести разделение переменных, используя метод Фурье.
5.3. Для этого представим функцию 
в виде произведения
, (15)
умножим обе части уравнения (14) слева на 
и перегруппируем слагаемые, включающие разные переменные:
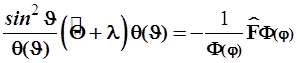(16)
Переменные 
и 
полностью разделились, поэтому правую и левую его части можно приравнять одной и той же постоянной. В результате получится два независимых уравнения
(17)
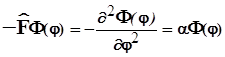(18)
5.4. Уравнение (17) – это уравнение Шредингера для плоского ротатора, где 
, и решение его было предметом обсуждения в разделе 3.2:
, где 
(19)
причём квантовое число m связано с квантованием проекции момента импульса на ось z, так как изменение угла описывает вращение вокруг этой оси:
6. Множитель
пока ещё не раскрыт, однако ясно, что каждая волновая функция отвечает состоянию с некоторым определенным фиксированным квадратом момента импульса или, что то же самое, с фиксированным модулем момента импульса. Обратим внимание читателя на то, что все преобразования, начавшись как векторные, завершаются расчетами в скалярной форме, и понятно, что из таких расчётов естественном путём вытекает квантование абсолютного значения векторной величины в виде квантования ее квадрата. Необходимое квантовое число назовем l и далее получим его значение.
7. Напоминаем, что волновые функции 
являются собственными функция-ми операторов 
и 
. На основании уравнений и можно записать
(20)
а из уравнений (4.58) и (4.70) следует
(21)
При вычитании (21) из (20) получаем операторное уравнение (22) с конкретным собственным значением 
т.е.
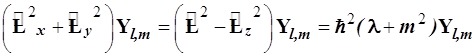. (22)
Целесообразно построить такую последовательность сомножителей из операторов сдвига, которая непосредственно приводила бы к ожидаемому результату (4.91).
8. Для этого исследуем произведение операторов вида 
.
Подставляя коммутатор, получим
(23)
Совершенно аналогично
(24)
или при совместной записи
(25)
В этих формулах привлекательно то, что результат произведения двух операторов сдвигов выражается через операторы с действительными собственными значениями, как это следует из сопоставления правых частей уравнений (22) – (20), с одной стороны, и уравнений (20) и (21) – с другой.
9. Все коммутационные соотношения операторов момента импульса и его проекций, найденные в этом разделе, удобно свести в одну таблицу 4.З. . В строках таблицы указаны левые операторы-сомножители, а в столбцах – правые. На пересечении строки и столбца находится коммутатор соответствующих операторов.
Обращаем внимание читателя на антисимметричный характер таблицы коммутаторов относительно главной диагонали, т.е. элементы, одинаково расположенные по разные стороны последней отличаются только знаками. Таким образом, при изменении порядка записи операторов–сомножителей коммутатор меняет знак.
Таблица 1. Коммутаторы операторов момента импульса
|
|
|
|
|
|
|
|
|
| 0 | 0 | 0 | 0 | 0 | 0 |
|
| 0 | 0 |
|
|
|
|
|
| 0 |
| 0 |
|
|
|
|
| 0 |
|
| 0 |
|
|
|
| 0 |
|
|
| 0 |
|
|
| 0 |
|
|
|
| 0 |
1\ 
Похожие работы
... В: (2.3) Теперь будет сформулирована простая задача спектральной оценки. Особое внимание будет уделено моделированию свойств процесса сбора данных, которые являются общими для многих задач обработки решеток. Эти свойства включают измерение корреляционной функции при конечном числе неравномерно распределенных точек и ограничения на область пространства частоты-воктора волны, в ...
... 1 – 4 (или части этих преобразований). Таким образом, справедливо следующее важное свойство аффинных преобразований плоскости: любое отображение вида (2.1) можно описать при помощи отображений, задаваемых формулами (2.3) – (2.11). Для эффективного использования этих известных формул в задачах компьютерной графики более удобной является их матричная запись. Матрицы, соответствующие случаям 1 – 3, ...
Бреславец, В.Н. Гамаюнов). Объектом исследования в данной исследовательской работе являются фигуры вращения правильных многогранников. Предмет исследования – объем тел вращения. Работая над темой, мне удалось собрать удивительно интересный материал о правильных многогранниках. Оказалось, что даже тайна мироздания связана с этими пятью правильными многогранниками. В процессе исследования были ...
... недостаточная ориентировка в частях собственного тела и недостаточность у них тонкой моторики. Глава II. Занятия конструированием в дошкольных образовательных учреждениях как фактор развития пространственных представлений старших дошкольников с задержкой психического развития 2.1 Обследование Данный анализ проводился на основе экспериментального изучения детей с ЗПР старшего дошкольного ...
0 комментариев