Навигация
Плотность жидкости при нормальной температуре кипения
Плотность жидкости при нормальной температуре кипения
Аддитивный метод ШредераПри изучении свойств органических жидкостей Шредером было сформулировано правило, в соответствии с которым при прогнозировании мольного объема чистой жидкости при нормальной температуре кипения следует сосчитать число атомов углерода, водорода, кислорода и азота в молекуле, добавить по единице на каждую двойную связь и сумму умножить на семь. При этом получаем мольный объем жидкости в см3/моль. Правило Шредера дает удивительно хорошие результаты для нормальных жидкостей - погрешность, как правило, не превышает 3-4% тон. Плотности сильно ассоциированных жидкостей прогнозируются с меньшей точностью. В дальнейшем аддитивный метод Шредера модифицировался самим автором и другими учеными. В табл. 6.5 приведены значения групповых вкладов в последней редакции Шредера и Ле Ба.
Таблица 6.5
Аддитивные составляющие для расчета молярных объемов Vb
органических веществ
| Тип атома, группы, связи | Составляющая, см3/моль | |
| Шредер | Ле Ба | |
| Углерод | 7 | 14,8 |
| Водород | 7 | 3,7 |
| Кислород (за исключением приведенных ниже случаев): | 7 | 7,4 |
| в метиловых сложных и простых эфирах | – | 9,1 |
| в этиловых сложных и простых эфирах | – | 9,9 |
| в высших сложных и простых эфирах | – | 11,0 |
| в кислотах | – | 12,0 |
| Тип атома, группы, связи | Составляющая, см3/моль | |
| Шредер | Ле Ба | |
| соединенный с S, P, N | – | 8,3 |
| Азот: | 7 | – |
| с двойной связью | – | 15,6 |
| в первичных аминах | – | 10,5 |
| во вторичных аминах | – | 12,0 |
| Бром | 31,5 | 27 |
| Хлор | 24,5 | 24,6 |
| Фтор | 10,5 | 8,7 |
| Иод | 38,5 | 37 |
| Сера | 21 | 25,6 |
| Кольцо: | – | |
| трехчленное | -7 | -6,0 |
| четырехчленное | -7 | -8,5 |
| пятичленное | -7 | -11,5 |
| шестичленное | -7 | -15,0 |
| нафталиновое | -7 | -30,0 |
| антраценовое | -7 | -47,5 |
| Двойная связь между атомами углерода | 7 | – |
| Тройная связь между атомами углерода | 14 | – |
Величина мольного объема жидкости при нормальной температуре кипения представлена в качестве функции критического объема:
![]() ,(6.13)
,(6.13)
где ![]() и
и ![]() выражены в см3/моль.
выражены в см3/моль.
Это простое соотношение хорошо прогнозирует ![]() для органических чистых жидкостей, погрешность не превышает 3% отн. при условии, что значения критического объема определены надежно.
для органических чистых жидкостей, погрешность не превышает 3% отн. при условии, что значения критического объема определены надежно.
Рассмотренные выше методы Шредера и Тина-Каллуса не распространяются на всю область насыщенных состояний жидкости. Они приложимы к одной точке в этой области - нормальной температуре кипения. Прогнозирование плотности насыщенной жидкости при любой температуре ниже ![]() может быть выполнено на основе некоторых уравнений состояния вещества, так, например, уравнения Бенедикта-Уэбба-Рубина для углеводородов. Однако целесообразнее использовать для этого специальные эмпирические корреляции, которые относительно просты и в большинстве случаев более точны.
может быть выполнено на основе некоторых уравнений состояния вещества, так, например, уравнения Бенедикта-Уэбба-Рубина для углеводородов. Однако целесообразнее использовать для этого специальные эмпирические корреляции, которые относительно просты и в большинстве случаев более точны.
Практически все корреляционные методы основаны на принципе соответственных состояний и требуют знания плотности насыщенной жидкости хотя бы при одной температуре. Поскольку даже такой минимум информации не всегда доступен, приходится прибегать к оценкам критической плотности вещества по его критическому объему. При отсутствии экспериментальных данных вычисление плотности может быть основано на коэффициенте сжимаемости жидкости при давлении насыщения, что рационально выполнять с использованием таблиц Ли-Кеслера (разд. 4). Ниже рассмотрены оба подхода.
Метод Ганна-ЯмадыМетод предназначен для прогнозирования молярного объема ![]() и плотности неполярных или слабополярных жидкостей
и плотности неполярных или слабополярных жидкостей ![]() только на линии насыщения. Он основан на принципе соответственных состояний. Для прогнозирования необходимо как минимум знать ацентрический фактор и критические температуру и давление. Предложенная авторами корреляция имеет вид
только на линии насыщения. Он основан на принципе соответственных состояний. Для прогнозирования необходимо как минимум знать ацентрический фактор и критические температуру и давление. Предложенная авторами корреляция имеет вид
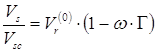 ,(6.14)
,(6.14)
где ![]() - безразмерный параметр,
- безразмерный параметр, ![]() - масштабирующий параметр,
- масштабирующий параметр, ![]() - ацентрический фактор.
- ацентрический фактор. ![]() и
и ![]() являются функциями приведенной температуры. Для расчета
являются функциями приведенной температуры. Для расчета ![]() рекомендованы корреляции двух видов:
рекомендованы корреляции двух видов:
при ![]()
![]() ;(6.15)
;(6.15)
при ![]()
![]() .(6.16)
.(6.16)
Расчет значения ![]() производится по одному уравнению для любой температуры в диапазоне
производится по одному уравнению для любой температуры в диапазоне ![]() :
:
![]() .(6.17)
.(6.17)
При расчете масштабирующего параметра рекомендованы следующие подходы.
Если известен молярный объем насыщенной жидкости ![]() или ее плотность при приведенной температуре
или ее плотность при приведенной температуре ![]() то расчет
то расчет ![]() построен на основе этих сведений:
построен на основе этих сведений:
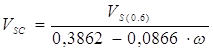 .(6.18)
.(6.18)
Если экспериментальные данные для ![]() отсутствуют, то расчет масштабирующего параметра выполняется по уравнению
отсутствуют, то расчет масштабирующего параметра выполняется по уравнению
![]() .(6.19)
.(6.19)
В большинстве случаев масштабирующий параметр близок по значению к критическому объему ![]() .
.
При наличии экспериментальных сведений о плотности интересующей насыщенной жидкости при некоторой температуре ![]() масштабирующий параметр
масштабирующий параметр ![]() может быть исключен из расчета, и задача сводится к решению уравнения
может быть исключен из расчета, и задача сводится к решению уравнения
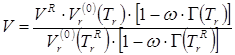 ,(6.20)
,(6.20)
где ![]() , а их участие в уравнении следует понимать как температурный уровень, при котором вычисляются
, а их участие в уравнении следует понимать как температурный уровень, при котором вычисляются ![]() и
и ![]() , а не как сомножители.
, а не как сомножители.
Метод Ганна-Ямады считается наиболее точным из имеющихся в настоящее время методов прогнозирования плотности насыщенной жидкости при Tr < 0,99. Несмотря на то, что он рекомендован авторами для неполярных или слабо полярных веществ, результативность его зачастую оказывается достаточной и в приложении к полярным жидкостям.
Пример 6.4
Методом Ганна-Ямады рассчитать плотность жидкого изобутилбензола, находящегося на линии насыщения в диапазоне 298-650 К. Критические параметры и ацентрический фактор вещества приведены выше.
Решение
Молярный объем вещества ![]() при избранной температуре вычисляется по уравнению (6.14).
при избранной температуре вычисляется по уравнению (6.14).
Поскольку экспериментальные данные для ![]() отсутствуют, то расчет масштабирующего параметра производим по уравнению (6.19):
отсутствуют, то расчет масштабирующего параметра производим по уравнению (6.19):
![]()
![]() 82,05·650·(0,2920-0,0967·0,378)/31 = 439 см3/моль.
82,05·650·(0,2920-0,0967·0,378)/31 = 439 см3/моль.
Результаты расчета плотности приведены в табл.6.6 и на рис. 6.9. Для 298 К имеем:
![]() = 298/650 = 0,458;
= 298/650 = 0,458;
![]() = 0,29607 – 0,09045·0,458 –0,04842·0,4582 = 0,244;
= 0,29607 – 0,09045·0,458 –0,04842·0,4582 = 0,244;
![]() = 0,33593–0,33953·0,458+1,51941·0,4582+1,11422·0,4584 = 0,354;
= 0,33593–0,33953·0,458+1,51941·0,4582+1,11422·0,4584 = 0,354;
![]() = 0,354·(1–0,378·0,244)·439 = 140,9 см3/моль;
= 0,354·(1–0,378·0,244)·439 = 140,9 см3/моль;
![]() = 134,222/140,9 = 0,952 г/см3 .
= 134,222/140,9 = 0,952 г/см3 .
Метод предназначен для прогнозирования плотностей жидкостей при любых давлениях. В приложении к плотности насыщенной жидкости метод заключается в следующем. Приведенная плотность жидкости, находящейся на линии насыщения, коррелирована с приведенной температурой:
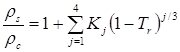 ,(6.21)
,(6.21)
где ![]() - мольная плотность насыщенной жидкости,
- мольная плотность насыщенной жидкости, ![]() - критическая плотность вещества,
- критическая плотность вещества, ![]() - приведенная температура.
- приведенная температура.
Коэффициенты ![]() являются функциями критического коэффициента сжимаемости и вычисляются по уравнениям
являются функциями критического коэффициента сжимаемости и вычисляются по уравнениям
![]() ;(6.22)
;(6.22)
![]() при
при ![]() ;(6.23)
;(6.23)
![]() при
при ![]() ;(6.24)
;(6.24)
![]() ;(6.25)
;(6.25)
![]() .(6.26)
.(6.26)
Пример 6.5
Методом Йена и Вудса рассчитать плотность жидкого изобутилбензола, находящегося на линии насыщения в диапазоне 298-650 К. Критический коэффициент сжимаемости изобутилбензола равен 0,28, критический объем составляет 480 см3/моль.
Решение
1. Вычисляем значения коэффициентов Kj:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
2. Критическая плотность изобутилбензола:
![]() г/см3 .
г/см3 .
3. Рассчитываем плотность жидкого изобутилбензола, находящегося на линии насыщения. Для 298 К имеем
![]() =0,8056 г/см3.
=0,8056 г/см3.
Фрагмент результатов расчета при других температурах приведен в табл. 6.6., на рис. 6.9. дается сопоставление их с полученными методом Ганна-Ямады и другими методами.
Метод Чью-ПраусницаМетод предназначен для прогнозирования плотности жидкости при любых давлениях. В приложении к жидкому состоянию на линии насыщения метод заключается в следующем. Отношение критической плотности c к плотности насыщенной жидкости s коррелировано с приведенной температурой и ацентрическим фактором:
 .
.
Для расчета ![]() предложены следующие эмпирические уравнения:
предложены следующие эмпирические уравнения:
![]()
![]() ;(6.27)
;(6.27)
![]()
![]() ;(6.28)
;(6.28)
![]()
![]() (6.29)
(6.29)
Пример 6.6
Методом Чью и Праусница рассчитать плотность жидкого изобутилбензола, находящегося на линии насыщения, в диапазоне 298-650 К. Критический объем составляет 480 см3/моль.
Решение
1. Вычисляем значения функций ![]() . Для 298 К имеем
. Для 298 К имеем
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() .
.
Похожие работы
... Обозначение трансмиссионных масел по ГОСТ 17479.2 – 85 ТМ – 5 – 18 Таблица №7 Таблица смазывания и заправки рабочих жидкостей автомобиля ВАЗ-2107 Номер на карте смазки в приложении Точка смазывания и заправки Колич. точек Объём, л Смазочный материал и Рабочая жидкость 6 Картер двигателя вклчая масленный фильтр Одна 3,75 Всесезонно м-8в или М-6з12г1 6 ...
... 907 Обозначение трансмиссионных масел по ГОСТ 17479.2 – 85 ТМ – 5 – 18 Таблица №7 Таблица смазывания и заправки рабочих жидкостей автомобиля ЗИЛ – 130 Точка смазывания и заправки Колич. точек Объём, л Смазочный материал и рабочая жидкость Картер двигателя Одна 8,5 Масло М-4З/6Б1(АСЗ-6) Подшипники жидкостного насоса ПП Смазка ЦИАТИМ-201 или ЛИТА Валик ...
... насыщенного пара при избранной для расчета температуре. Для каждой из названных областей P-V-T пространства существуют самостоятельные подходы к прогнозированию плотности. Прогнозирование плотности индивидуальных веществ с использованием коэффициента сжимаемости Пример 6.1 Для изобутилбензола, имеющего критическую температуру 650 К, критическое давление 31 атм и ацентрический фактор 0,378, ...
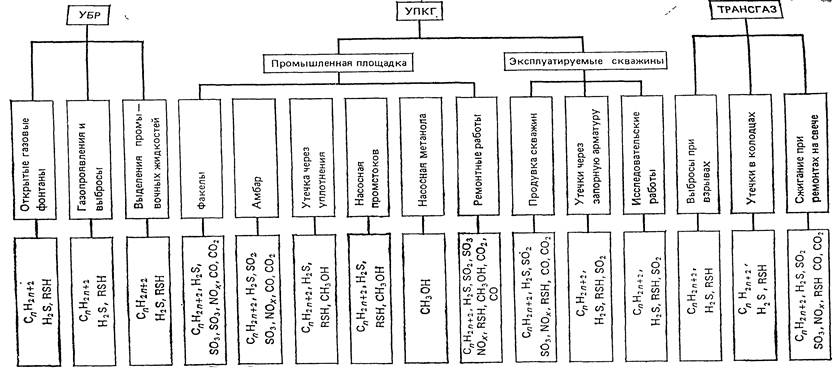
... от кислых газов (м3/с) Концентрированные кислые газы, полученные при регенерации метанола, общим потоком подаются на установку переработки кислых газов с получением товарной серы. Из практики известно, что в промышленных условиях при очистке природного газа от кислых газов метанолом с последующим выделением кислых газов при регенерации, получают концентрированный кислый газ, содержащий 58% Н2S ...

0 комментариев