Розкриття невизначеностей за правилом Лопіталя

Міністерство охорони здоров’я України

Житомирський фармацевтичний коледж

ім. Г.С. Протасевича

Реферат

на тему:

“ Розкриття невизначеностей за правилом Лопіталя”

 

Роботу виконала

Студентка 211 групи

Піщук Олеся

Викладач:

Виговська В.Г.

Отриманий бал:

_____________

м. Житомир – 2006

 

План

 

І. Розкриття невизначеностей з використанням правила Лопіталя.

1) Правило Лопіталя.

а) Наслідок.

б) Приклад 1.

2) Розкриття невизначеностей виду: ∞-∞; 0∙∞; 1^∞; 0⁰; ∞⁰.

а) Приклад 2.

б) Приклад 3.

в) Приклад 4.

Список використаної літератури.

І. Розкриття невизначеностей з використанням правила Лопіталя.

 

Лопіталь де Гійом Франсуа (1661-2.02.1704 рр.). Французький математик, член Парижської АН, народився в Парижі, вивчав математику під керівництвом У. Бернуллі. Видав перший друкований підручник по диференціальному обчисленню – “Аналіз нескінченно малих” (1696р.). В підручнику є правило Лопіталя – правило знаходження межі дробу, чисельник і знаменник якого прямує до 0. Крім того, він створив курс аналітичної геометрії конічних перетинів. Йому також належить дослідження і розвиток за допомогою математичного аналізу декількох важких задач по геометрії і механіці, а також одне із рівнянь знаменитої задачі о браністохроні.

 

1.  Правило Лопіталя.

Нехай виконані умови:

1.  функції f(х) та g(х) визначені і диференційовані в колі точки х₀;

2.  частка цих функцій  в точці х₀ має невизначеність вигляду  або ;

3.  існує .

Тоді існує  і виконує рівність:

(1)

 

а) Наслідок.

Нехай:

1. Визначені в колі точки х₀ функції f(х),  g(х) та їх похідні до n-го порядку включно;

2. Частки , , …,  мають невизначеність вигляду  або ;

3. Існує , тоді

(2)

 

б) Приклад 1.

Знайти: .

Розв’язання:

Функції  та  визначені з усіма своїми похідними в околі точки х=0.

Маємо:

.

2) Розкриття невизначеностей виду: ∞-∞; 0∙∞; 1^∞; 0⁰; ∞⁰.

Існують прийоми, що дозволяють зводити вказані невизначеності до невизначеностей вигляду  або , які можна розкривати з використанням правила Лопіталя.

1.   Нехай  і , тоді

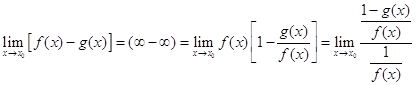(3)

За умовою  при , тому  при .

Якщо  не прямує до 0 при , то границя в правій частині (3) не існує, а тому і границя лівої частини (3) не існує.

Якщо  при , то вираз 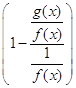 має невизначеність .

2. Нехай , , тоді  має невизначеність вигляду  при .

В цьому випадку поступають так:

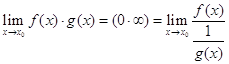
Під знаком останньої границі маємо невизначеність .

3. Нехай ,  при . Тоді  має невизначеність вигляду .

Позначимо . Шляхом логарифмування цієї рівності одержимо:

Отже, обчислення натурального логарифма границі  зводиться до розкриття невизначеності вигляду .

4. Невизначеності вигляду  та  зводять до невизначеностей  або  шляхом логарифмування аналогічно до невизначеності вигляду .

а) Приклад 2.

Знайти границю .

Розв’язання:

Функції  та  диференційовані, а їх частка  має невизначеність вигляду  при .

Використовуючи правило Лопіталя, одержимо:

.

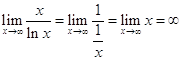б) Приклад 3.

Знайти границю .

Розв’язання:

В цьому випадку маємо невизначеність вигляду . Позначимо  і про логарифмуємо цю рівність. Одержимо:

, тобто невизначеність вигляду . Використовуючи правило Лопіталя, одержимо:

.

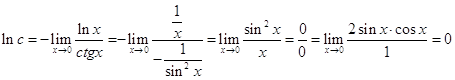Отже, .

в) Приклад 4.

Знайти границю .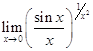

В цьому випадку маємо невизначеність вигляду . Нехай 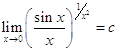. Логарифмуючи цю рівність, одержимо:

 .

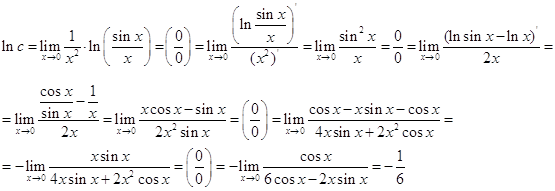Чотири рази застосували правило Лопіталя.

Отже, маємо:

 

 

 

 

 

 

 

 

 

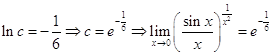
Список використаної літератури:

 

1.                Кривуца В.Г., Барковський В.В., Барковська Н.В. К.82. Вища математика. Практикум. Навчальний посібник.–Київ: Центр навчальної літератури, 2005.–536с.

2.                Бородин А.И., Бугай А.С., Биографический словарь деятелей в области математики. Радянська школа 1979.

3.                Алгебра и начала анализа: В 2-х ч./ Под. ред. Г.Н. Яковлева.–2-е изд. –К.: Вища шк., Головное изд-во, 1984.–Ч.2. 293с.