Вариант №9
№1. Решить систему линейных уравнений по правилу Крамера, с помощью обратной матрицы
a) По правилу Крамера.
![]()
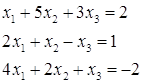


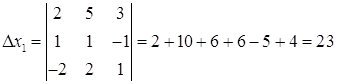


![]() ;
;
б) С помощью обратной матрицы.
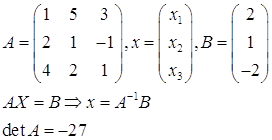
Алгебраические дополнения:
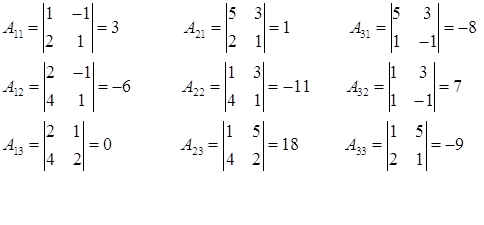
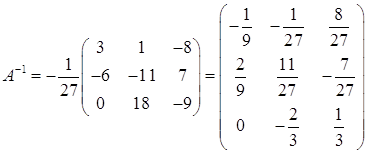
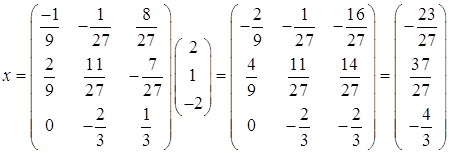
![]()
№ 2. Вычислить определитель
а) С помощью теоремы Лапласа. б) Предварительно упростив, получив нули в какой либо строке (столбце).
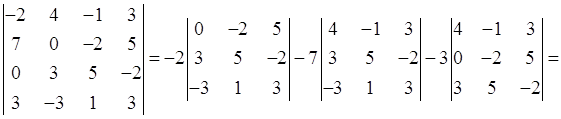
![]()
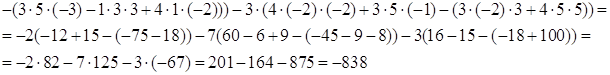
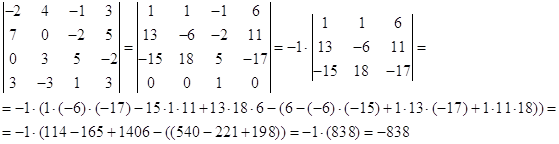
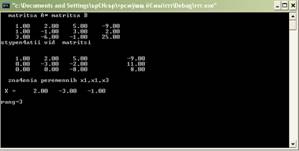
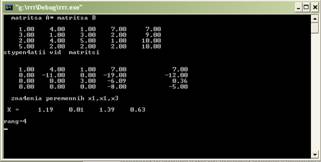
№3. Найти ранг матрицы
a) С помощью элементарных преобразований
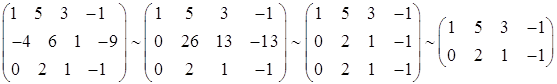
б) Найти ранг матрицы методом окаймления миноров
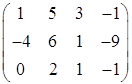
Решение. Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) М 1 = 1, расположенный в первой строке и первом столбце. Окаймляя при помощи второй строки и третьего столбца, получаем минор M 2=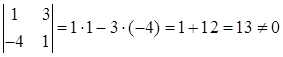 , отличный от нуля. Переходим теперь к минорам 3-го порядка, окаймляющим М 2. Их всего два (можно добавить второй столбец или четвертый). Вычисляем их:
, отличный от нуля. Переходим теперь к минорам 3-го порядка, окаймляющим М 2. Их всего два (можно добавить второй столбец или четвертый). Вычисляем их:
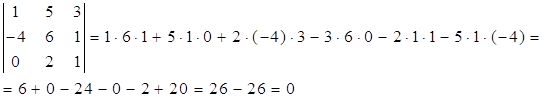
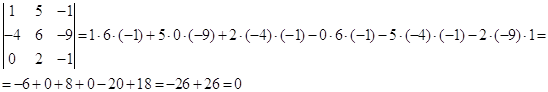
Таким образом, все окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум.
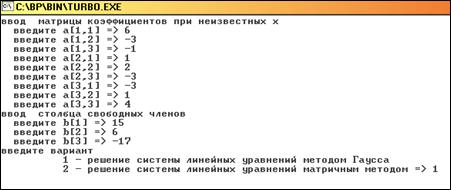
№4. Дана система уравнений:
a) исследовать на совместимость б) Найти общее решение методом Гауса и записать два частных.
![]()
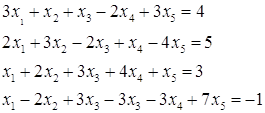

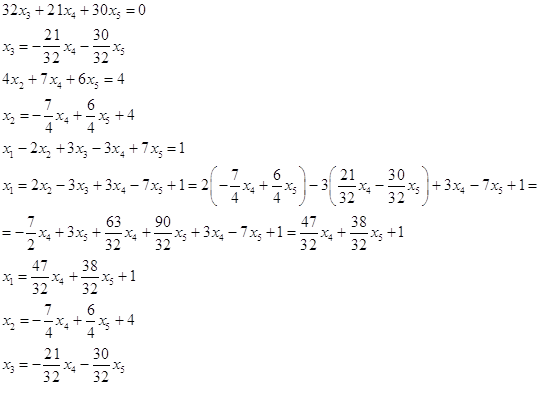
Частные решения:

№5. Найти фундаментальную систему решений однородной системы уравнений
![]()
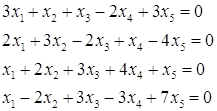
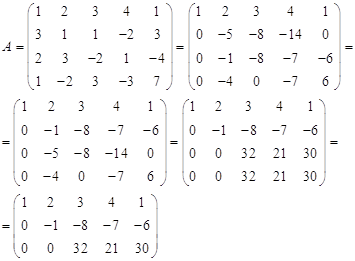
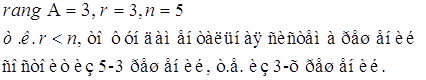
![]()

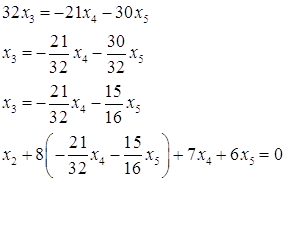
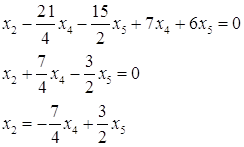

№ 6
a) Найти площадь ABC
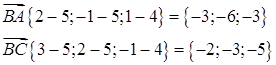
Найдем векторное произведение ![]() :
:
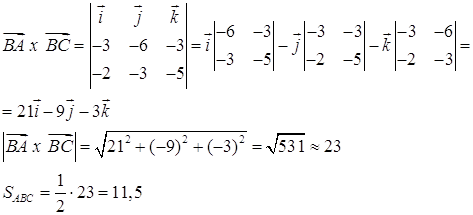
б) Составим уравнение плоскости ABC:
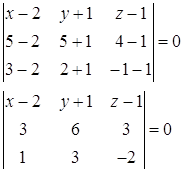
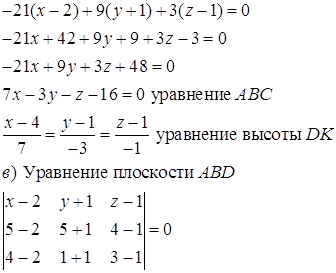
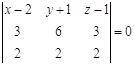
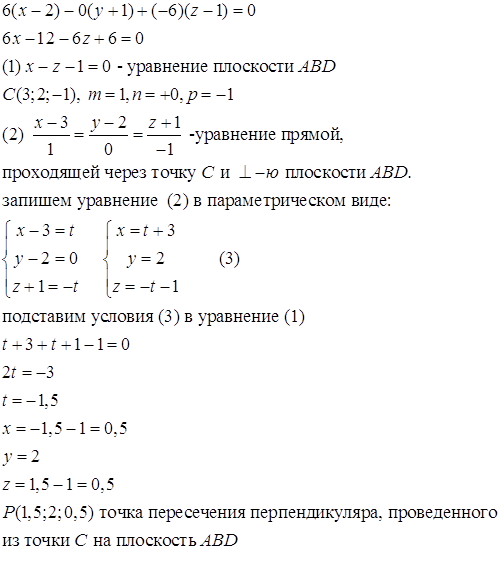
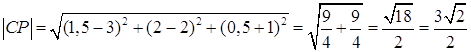
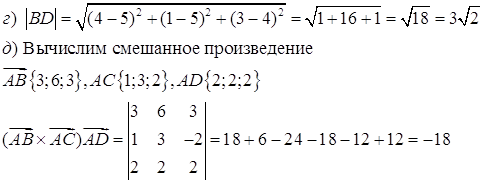
Объем параллелепипеда, построенного на трёх некомпланарных векторах ![]() , равен абсолютной величине их смешанного произведения, т.е. 18. Объем тетраэдра
, равен абсолютной величине их смешанного произведения, т.е. 18. Объем тетраэдра ![]()
e) Найти величину плоского угла при вершине С плоскости ABC

Похожие работы
... + аm2с2 + …+ аmnсn где c1, c2,..., сп — коэффициенты линейных комбинаций. Таким образом, системе (14) удовлетворяют значения x1 = c1,..., хп = сп, следовательно, она совместна. Теорема доказана. Доказанная теорема совместности системы линейных уравнений называется теоремой Кронекера – Капелли. Пример 1. Рассмотрим систему 5x1 – x2 + 2x3 + x4 = 7; 2x1 + x2 – 4x3 – 2x4 = 1; x1 – 3x2 + ...
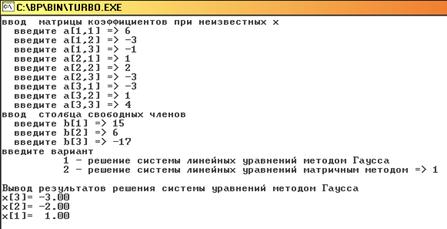
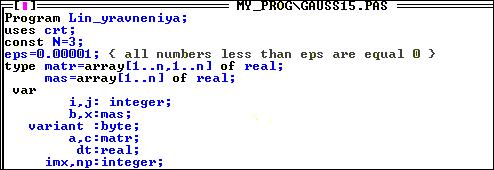
... 4.Исходный текст программы Составить программу решения систем линейных алгебраических уравнений с квадратной невырожденной матрицей порядка n методом Гаусса с использованием языка С++ . // Решение системы линейных уравнений методом Гаусса. #include<io.h> #include "stdio.h" #include "conio.h" #include <windows.h> #include <iostream> #include <time.h> #include ...
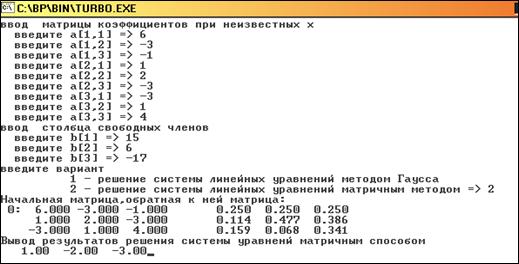
... строке матрицы i2-ю, умноженную на число r; процедура MultMatr предназначена для умножения матриц. Функция Sign используется для изменения знака на противоположный при вычислении обратной матрицы. Программа настроена на решение системы 3-х линейных уравнений с тремя неизвестными. Чтобы решить систему из 2-х уравнений с 2-мя неизвестными необходимо в программе изменить значение константы N с ...
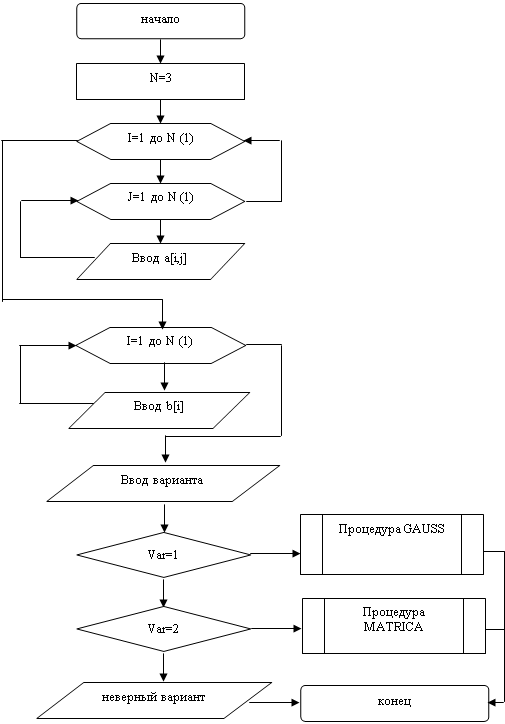
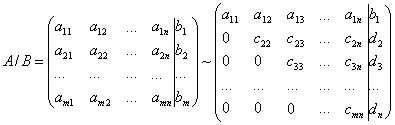
... к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. Рассмотрим решение системы (1) m линейных уравнений с nпеременными в общем виде: (3) Если m=n, то рассмотрим расширенную матрицу. Учитывая правую часть, приведем данную матрицу к треугольному виду: Ситема линейных ...
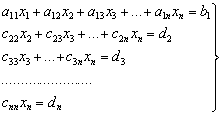
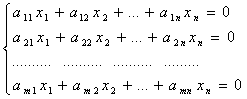
0 комментариев