( технический университет )
Филиал “Взлёт”
Курсовая работа по дисциплине "Теория вероятности и математическая статистика"“Теория вероятности”
Выполнил студент группы ДР-2:
Архипов А.В.
Проверил преподаватель:
Егорова Т. П.
г. Ахтубинск 2004 г
Задание 1
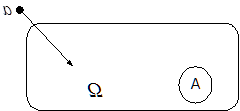
Проверка выполнимости теоремы Бернулли на примере надёжности электрической схемы.
Формулировка теоремы Бернулли: “Частота появления события в серии опытов сходится по вероятности к вероятности данного события”.

p1 = 0.9
p2 = 0.8
p3 = 0.9
p4 = 0.8
p5 = 0.9
p6 = 0.9
Проверка теоремы с помощью программы:
Текст программы:
Program bernuli;
Uses CRT;
Var op,i,j,m,n:integer;
a,pp:real;
p:array[1..6] of real;
x:array[1..6] of byte;
Begin
ClrScr;
Randomize;
p[1]:=0.9; p[2]:=0.8; p[3]:=0.9; p[4]:=0.8; p[5]:=0.9; p[6]:=0.9;
for op:=1 to 20 do begin
n:=op*100; m:=0;
write(' n=',n:4);
for i:=1 to n do begin
for j:=1 to 6 do begin
x[j]:=0;
a:=random;
if a<p[j] then x[j]:=1;
end;
if ((((((x[1]=1) and (x[2]=1)) or (x[3]=1)) and (x[4]=1)) or (x[5]=1)) and (x[6]=1)) then m:=m+1
end;
pp:=m/n;
writeln(' M=',m:4,' P*=',pp:3:6);
End;
Readln;
end.
Результаты работы программы:
Опытов: Мсходы: Вер-ть:
n= 100 M= 89 P*=0.89
n= 200 M= 173 P*=0.86
n= 300 M= 263 P*=0.88
n= 400 M= 360 P*=0.90
n= 500 M= 434 P*=0.87
n= 600 M= 530 P*=0.88
n= 700 M= 612 P*=0.87
n= 800 M= 704 P*=0.88
n= 900 M= 784 P*=0.87
n=1000 M= 865 P*=0.86
n=1100 M= 985 P*=0.90
n=1200 M=1062 P*=0.89
n=1300 M=1165 P*=0.90
n=1400 M=1238 P*=0.88
n=1500 M=1330 P*=0.89
n=1600 M=1418 P*=0.89
n=1700 M=1471 P*=0.87
n=1800 M=1581 P*=0.88
n=1900 M=1670 P*=0.88
n=2000 M=1768 P*=0.88
Вер. в опыте: p= 0.88
Проверка вручную:
Первый способ:
![]()
Второй способ:
![]()
Вывод: Теорема Бернулли верна.
Задание 2
Методом кусочной аппроксимации смоделировать случайную величину, имеющую закон распределения Коши, заполнить массив из 300 точек.
Теория:
Метод кусочной аппроксимации заключается в том, что для формирования одного случайного числа из последовательности с заданным законом распределения необходимо дважды использовать датчик случайных чисел. Процедура получения случайного числа yi сводиться к:
1. Случайный выбор интервала (определение значения aj)
2. Случайный выбор «b» из этого интервала
3. Формирование случайного числа в соответствии с формулой ![]()
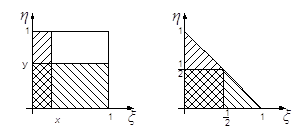
При выборе интервала на первом шаге процедуры должна учитываться плотность распределения. С этой целью ее кусочно-линейно аппроксимируют отрезками прямых, параллельных оси абсцисс (рис.1.)
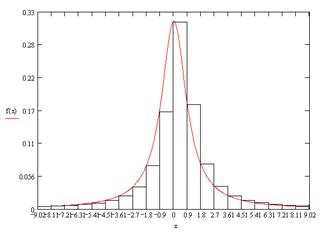
Рис.1. Кусочно-линейно аппроксимированный график плотности распределения по закону Коши.
Количество интервалов разбиения области определения случайной величины обычно выбирается достаточно большим (именно поэтому в данной Курсовой работе было использовано разбиение на 400 интервалов).
Решение:
Построим график плотности распределения по закону Коши (![]() ):
):
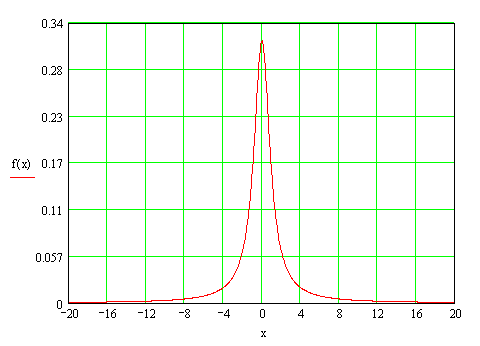
Рис.2. График распределения Коши.
Необходимо разбить интервал от –20 до 20 на n подинтервалов (в данном случае n=40) и вычислить вероятность попадания на каждый из этих подинтервалов. После этого составить массив [a1,aj], так чтобы a1=0, a ![]() , случайно сгенерировать значение числа «b» из промежутка от 0 до 1, найти номер интервала в который она попадет и второй раз используя датчик случайных чисел сгенерировать случайную добавку «b». Для выполнения этих действий составим программу в среде Turbo Pascal 7.1.
, случайно сгенерировать значение числа «b» из промежутка от 0 до 1, найти номер интервала в который она попадет и второй раз используя датчик случайных чисел сгенерировать случайную добавку «b». Для выполнения этих действий составим программу в среде Turbo Pascal 7.1.
Программа позволяющая смоделировать СВ, имеющую закон распределения Коши:
Program tvmslab2;
Uses CRT,GRAPH;
Type mas=array[1..40] of real;
label 10;
const a:mas=(0.0008,0.0009,0.001,0.0011,0.0013,0.0015,0.0017,0.002,0.0024,
0.00287,0.0035,0.0043,0.0056,0.0074,0.01,0.015,0.024,0.045,0.102,0.25,0.25,
0.102, 0.045,0.024,0.015,0.01,0.0074,0.0056,0.0043,0.0035,0.00287,0.0024,0.002
0.0017,0.0015,0.0013,0.0011,0.001,0.0009,0.0008);
Xmax=20; Xmin=-20;
n=300; k=40; xn=70; xm=550; yn=180; ym=140;
Var i,j:integer;
q:boolean;
a1,y,x,e,dh,t,Mmax,hmax,t1,t2,b,Mxx,Dxx,Skx,Qxx,Exx:real;
r,d,x1,x2,y1,y2:integer;
m,xi,pix,hi,h:array[1..300] of real;
o,l:array[1..41] of real;
b1:array[0..300] of real;
st:string;
Begin
clrscr;
randomize;
o[1]:=0;
for i:=1 to 41 do begin
o[i+1]:=o[i]+a[i];
end;
x:=-20;
for i:=1 to 41 do begin
l[i]:=x;
x:=x+1;
end;
writeln(' Массив имеющий закон распределения Коши:')
writeln;
for j:=1 to 300 do begin
a1:=random;
for i:=1 to 41 do begin
if (a1>o[i]) and (a1<o[i+1]) then goto 10;
end;
10: b1[j]:=random+l[i];
write(' ',b1[j]:1:2);
if j mod 10= 0 then writeln;
if j mod 210= 0 then readln;
end;
readln;
end.
Результат работы программы:
Массив имеющий закон распределения Коши:
3.83 -9.36 0.79 0.22 -0.32 0.46 -0.73 20.98 -0.44 -1.74 0.02 0.70 -1.98 0.77 -9.79 3.24 0.36 -1.04 -4.28 2.71 -1.82 -0.92 -3.36 -0.65 0.37 -0.15 0.36 -0.61 0.76 20.56 -1.81 -8.94 0.26 0.40 1.62 0.59 -0.41 1.69 -0.02 0.29 0.61 0.32 0.86 -1.24 -1.87 -0.84 2.95 0.04 -0.63 1.54 0.53 -1.07 -0.08 -2.15 3.43 -0.66 -2.70 -0.87 0.64 0.65 0.04 3.76 -2.54 -3.80 2.40 1.22 -0.84 8.86 0.54 3.91 -0.70 -5.46 -1.64 -0.01 -0.52 -1.08 -2.16 -0.66 0.83 -1.88 1.97 0.55 3.84 -0.51 0.22 20.98 -3.00 0.46 -0.40 -2.10 0.78 20.46 -4.76 -0.36 1.30 3.85 -0.41 19.88 0.55 -1.05 0.14 -15.07 -0.87 0.18 -3.28 1.10 -0.42 -3.83 1.35 -3.82 -0.72 -1.02 -0.35 -0.13 -0.10 0.40 0.85 0.40 -0.62 1.28 -2.68 -1.88 -2.43 0.94 1.67 20.21 -0.70 -0.39 -3.56 -0.60 -3.86 -0.99 -6.71 0.79 1.62 -1.11 2.87 0.74 1.08 -0.29 -0.90 -0.22 0.04 -6.63 0.13 -0.36 -10.82 -3.04 2.81 -0.73 -0.16 0.61 -0.25 4.00 -0.93 -7.58 -0.09 0.69 0.30 2.38 0.79 11.03 -0.44 -0.56 11.12 -1.22 1.17 0.60 -1.78 -2.78 -0.85 -0.98 -1.21 3.51 0.05 0.29 -8.62 0.26 -0.56 1.68 -1.65 13.02 -0.11 0.50 -0.58 4.98 0.57 -0.51 0.78 -0.43 -1.62 0.27 0.75 0.29 20.65 0.91 0.01 3.46 -0.58 -0.50 9.42 -0.88 -1.78 0.81 1.35 -0.03 3.53 11.99 0.63 -1.65 20.66 0.36 -0.01 -0.68 0.31 0.28 16.13 -1.24 -0.36 0.99 -1.65 0.58 1.88 -0.35 0.66 0.94 1.56 0.31 0.58 0.61 -0.73 1.04 -0.61 -1.73 -1.02 -7.95 21.00 -0.98 20.94 -0.03 0.36 0.82 -2.91 1.03 0.47 -0.91 6.13 1.49 0.91 6.30 -0.93 1.03 -1.07 1.70 -0.63 -8.84 -1.87 0.01 2.63 -1.20 1.73 -1.71 -12.13 0.89 3.30 -0.24 0.36 18.97 9.16 0.77 -0.02 -0.03 -2.71 -1.20 -0.79 0.95 -0.18 0.50 5.61 -0.04 0.05 0.81 0.93 20.94 -0.91 20.17 1.70 1.66 -0.99 -0.25 -0.51 0.79 20.58 1.78 2.62 0.99 -1.45 0.89 -0.48 -0.98
Вывод: Используя данный метод можно формировать случайные величины со сколь угодно сложным законом распределения. Недостаток – необходимость некоторой подготовительной работы перед непосредственным применением процедуры и двукратное применение датчика случайных чисел для розыгрыша одного значения случайного числа Y.
Задание 3
Критерием Пирсона проверить, что данный массив имеет соответствующий закон распределения.
Для построения гистограммы и нахождения числовых характеристик, необходимо составить статистический ряд:
Статистический ряд
m[1]=0.00 x[1]=-19.5 pi[1]=0.0000 hi[1]=0.0000
m[2]=0.00 x[2]=-18.5 pi[2]=0.0000 hi[2]=0.0000
m[3]=0.00 x[3]=-17.5 pi[3]=0.0000 hi[3]=0.0000
m[4]=0.00 x[4]=-16.5 pi[4]=0.0000 hi[4]=0.0000
m[5]=1.00 x[5]=-15.5 pi[5]=0.0033 hi[5]=0.0033
m[6]=0.00 x[6]=-14.5 pi[6]=0.0000 hi[6]=0.0000
m[7]=0.00 x[7]=-13.5 pi[7]=0.0000 hi[7]=0.0000
m[8]=1.00 x[8]=-12.5 pi[8]=0.0033 hi[8]=0.0033
m[9]=0.00 x[9]=-11.5 pi[9]=0.0000 hi[9]=0.0000
m[10]=1.00 x[10]=-10.5 pi[10]=0.0033 hi[10]=0.0033
m[11]=2.00 x[11]=-9.5 pi[11]=0.0067 hi[11]=0.0067
m[12]=3.00 x[12]=-8.5 pi[12]=0.0100 hi[12]=0.0100
m[13]=2.00 x[13]=-7.5 pi[13]=0.0067 hi[13]=0.0067
m[14]=2.00 x[14]=-6.5 pi[14]=0.0067 hi[14]=0.0067
m[15]=1.00 x[15]=-5.5 pi[15]=0.0033 hi[15]=0.0033
m[16]=2.00 x[16]=-4.5 pi[16]=0.0067 hi[16]=0.0067
m[17]=8.00 x[17]=-3.5 pi[17]=0.0267 hi[17]=0.0267
m[18]=11.00 x[18]=-2.5 pi[18]=0.0367 hi[18]=0.0367
m[19]=32.00 x[19]=-1.5 pi[19]=0.1067 hi[19]=0.1067
m[20]=79.00 x[20]=-0.5 pi[20]=0.2633 hi[20]=0.2633
m[21]=83.00 x[21]=0.5 pi[21]=0.2767 hi[21]=0.2767
m[22]=26.00 x[22]=1.5 pi[22]=0.0867 hi[22]=0.0867
m[23]=8.00 x[23]=2.5 pi[23]=0.0267 hi[23]=0.0267
m[24]=12.00 x[24]=3.5 pi[24]=0.0400 hi[24]=0.0400
m[25]=1.00 x[25]=4.5 pi[25]=0.0033 hi[25]=0.0033
m[26]=1.00 x[26]=5.5 pi[26]=0.0033 hi[26]=0.0033
m[27]=2.00 x[27]=6.5 pi[27]=0.0067 hi[27]=0.0067
m[28]=0.00 x[28]=7.5 pi[28]=0.0000 hi[28]=0.0000
m[29]=1.00 x[29]=8.5 pi[29]=0.0033 hi[29]=0.0033
m[30]=2.00 x[30]=9.5 pi[30]=0.0067 hi[30]=0.0067
m[31]=0.00 x[31]=10.5 pi[31]=0.0000 hi[31]=0.0000
m[32]=3.00 x[32]=11.5 pi[32]=0.0100 hi[32]=0.0100
m[33]=0.00 x[33]=12.5 pi[33]=0.0000 hi[33]=0.0000
m[34]=1.00 x[34]=13.5 pi[34]=0.0033 hi[34]=0.0033
m[35]=0.00 x[35]=14.5 pi[35]=0.0000 hi[35]=0.0000
m[36]=0.00 x[36]=15.5 pi[36]=0.0000 hi[36]=0.0000
m[37]=1.00 x[37]=16.5 pi[37]=0.0033 hi[37]=0.0033
m[38]=0.00 x[38]=17.5 pi[38]=0.0000 hi[38]=0.0000
m[39]=1.00 x[39]=18.5 pi[39]=0.0033 hi[39]=0.0033
m[40]=1.00 x[40]=19.5 pi[40]=0.0033 hi[40]=0.0033
Построим гистограмму:
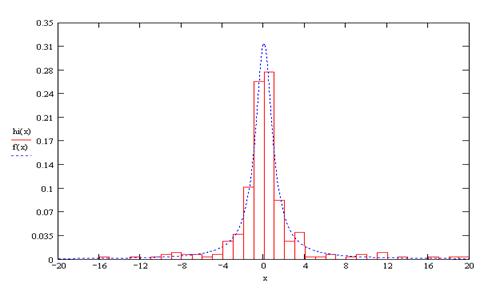
Рис.3. Гистограмма распределения по закону Коши.
По данным статистического ряда вычислим числовые характеристики:
Числовые характеристики:
![]() - статистическое математическое ожидание
- статистическое математическое ожидание
![]() - статистическая дисперсия
- статистическая дисперсия
![]() - статистическое среднеквадратическое отклонение
- статистическое среднеквадратическое отклонение
![]() - скошенность
- скошенность
![]() - эксцесс
- эксцесс
Для нахождения ![]() необходимо вычислить Pi (вероятности попадания на каждый из интервалов). Вероятность попадания может быть найдена как площадь криволинейной трапеции, ограниченной концами этого интервала слева и справа, и графиком плотности распределения сверху:
необходимо вычислить Pi (вероятности попадания на каждый из интервалов). Вероятность попадания может быть найдена как площадь криволинейной трапеции, ограниченной концами этого интервала слева и справа, и графиком плотности распределения сверху:
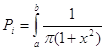
По найденной частоте и вероятности, вычислим значение ![]() :
:
![]()
Т.к. число степеней свободы r = 7, а уровень значимости p = 0.1, следовательно значение ![]() будет равным 12.02.
будет равным 12.02.
Вывод: Таким образом, сравнив значения ![]() и
и ![]() получим, что
получим, что ![]() , а, следовательно, нет оснований отвергнуть гипотезу о распределении случайной величины по закону Коши.
, а, следовательно, нет оснований отвергнуть гипотезу о распределении случайной величины по закону Коши.
Литература
1. Е. С. Венцель “Теория вероятности”
2. Г.М. Погодина “Лабораторные работы по курсу Теория вероятностей и статистических решений”
3. Курс лекций по Теории вероятности
Похожие работы
... Доказать: По определению второй смешанной производной. Найдем по двумерной плотности одномерные плотности случайных величин X и Y. Т.к. полученное равенство верно для всех х, то подинтегральные выражение аналогично В математической теории вероятности вводится как базовая формула (1) ибо предлагается, что плотность вероятности как аналитическая функция может не существовать. Но т.к. в нашем ...
... равна 0,515). Конец 19 в. и 1-я половина 20 в. отмечены открытием большого числа статистических закономерностей в физике, химии, биологии и т.п. Возможность применения методов теории вероятностей к изучению статистических закономерностей, относящихся к весьма далёким друг от друга областям науки, основана на том, что вероятности событий всегда удовлетворяют некоторым простым соотношениям, о ...
... {ξn (ω )}¥n=1 . Поэтому, во-первых, можно говорить о знакомой из математического анализа (почти) поточечной сходимости последовательностей функций: о сходимости «почти всюду», которую в теории вероятностей называют сходимостью «почти наверное». Определение 46. Говорят, что последовательность с. в. {ξn } сходится почти наверное к с. в. ξ при n ® ¥ , и пишут: ξn ...
... ничего другого, кроме как опять же события и . Действительно, имеем: *=, *=, =, =. Другим примером алгебры событий L является совокупность из четырех событий: . В самом деле: *=,*=,=,. 2.Вероятность. Теория вероятностей изучает случайные события. Это значит, что до определенного момента времени, вообще говоря, нельзя сказать заранее о случайном событии А произойдет это событие или нет. Только ...





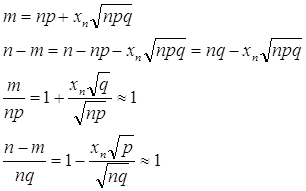
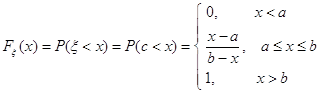
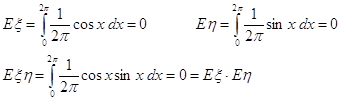
0 комментариев