Определение стоимости основных фондов

Контрольные задания

 

Вариант 2.

1.         Выполнить задачу №1 (n=10).

2.         По данным задачи №1 определить:

А) среднее квадратическое отклонение;

Б) коэффициент вариации;

В) модальный интервал распределения и моду.

3.         Выполнить задачу №2.

4.         Выполнить задачу №3.

5.         По данным задачи №3 рассчитать абсолютное изменение стоимости товаров, в том числе за счет изменения физического объема и за счет изменения цен:

1.Выполнить задачу №1 (n=10).

Задача № 1.

Имеются следующие данные о стоимости основных фондов предприятий, млн. руб.

Таблица 1.

99,0	80,3	103,1	115,4	84,5	93,4	103,1	106,4	95,6	86,1
78,1	105,3	96,4	82,7	118,1	98,8	125,7	89,9	140,0	104,5
100,1	123,1	95,3	79,1	107,1	84,4	108,8	96,4	117,0	85,6
95,0	109,3	80,7	105,8	90,5	97,5	119,0	107,7	90,7	96,1
70,2	81,0	111,3	75,3	99,1	92,0	72,2	109,1	89,3	70,0

1.Построить интервальный вариационный ряд с равными интервалами, выделив n групп предприятий по величине стоимости основных фондов.

2.Изобразить полученный вариационный ряд графически в виде гистограммы и полигона распределения.

3.Построить кумуляту распределения предприятий по величине стоимости основных фондов.

4.Определить по данным вариационного ряда среднюю стоимость основных фондов.

Решение.

1.Построим интервальный вариационный ряд с равными интервалами, выделив 10 групп предприятий по величине стоимости основных фондов.

Чтобы определить величину интервала в группе, необходимо найти разность между максимальным и минимальным значениями признака ( в нашем случае стоимости основных фондов предприятий) и разделим её на число выделяемых групп. Обозначим величину интервала через h, следовательно, h= (140-70)/10=7 (млн. руб.)

Выделим теперь группы с интервалом 7 млн. руб. и подсчитаем число предприятий в каждой группе (в виде таблицы):

Таблица 2.

Стоимости основных фондов предприятий, млн. руб.	Число предприятий fi	Накопленные (кумулятивные) частоты
70-77 77-84 84-91 91-98 98-105 105-112 112-119 119-126 126-133 133-140	4 6 8 9 7 9 4 2 0 1	4 10 18 27 34 43 47 49 49 50
Всего	50

2.Изобразим полученный вариационный ряд графически в виде гистограммы и полигона распределения

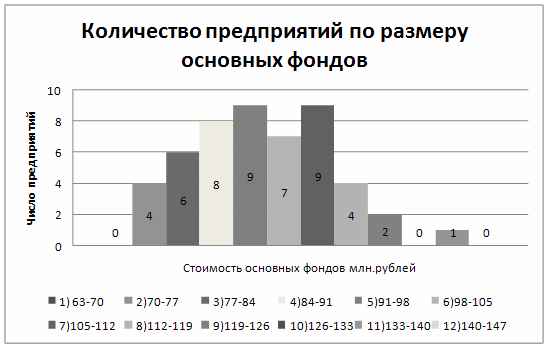
Рис.1. Гистограмма и полигон распределения 50-и предприятий по размеру основных фондов

3.Построим кумуляту распределения предприятий по величине стоимости основных фондов.

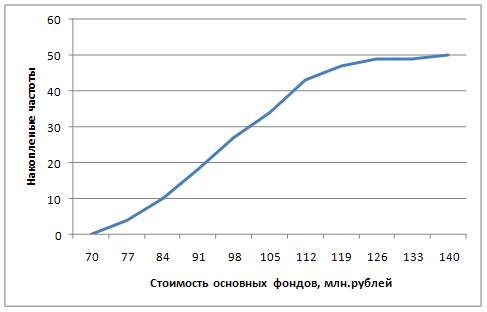
Рис.2 Кумулята распределения 50-и предприятий по размеру основных фондов

4.Определим по данным вариационного ряда среднюю стоимость основных фондов.

Для определения средней стоимости основных фондов нам необходимо добавить в таблицу 2 дополнительно два столбца, а именно Середина интервала (xi) и столбец произведения среднего интервала на число предприятий (fi), то есть (xi*f i). В связи с тем что, нам даны не точные цифры, а диапазоны и последняя колонка, следовательно, в данной ситуации мы должны использовать среднюю арифметическую взвешенную.

Формула средней арифметической взвешенной следующая:

∑ xi*f i

x = ————

∑ f i

Таблица 3.

Стоимости основных фондов предприятий, млн. руб.	Середина интервала xi	Число предприятий fi	Накопленные (кумулятивные) частоты	xi*f i
70-77 77-84 84-91 91-98 98-105 105-112 112-119 119-126 126-133 133-140	73,5 80,5 87,5 94,5 101,5 108,5 115,5 122,5 129,5 136,5	4 6 8 9 7 9 4 2 0 1	4 10 18 27 34 43 47 49 49 50	294 483 700 850,5 710,5 976,5 462 245 0 136,5
Всего		50		4858

Посчитаем среднюю стоимость основных фондов:

∑ xi*f i 4858

x = ———— = ———— = 97,16 (млн. руб.)

∑ f i 50

Ответ: средняя стоимость основных фондов указанных в Таблице 1 предприятий составляет 97,16 млн. руб.

2. По данным задачи №1 определить:

А) среднее квадратическое отклонение;

Б) коэффициент вариации;

В) модальный интервал распределения и моду.

Решение.

А) Определим среднее квадратическое отклонение (σ).

В нашем случае применим формулу для вариационного ряда:

∑ (xi - x) f i

σ = √ —————

∑ f i

а) нам известна x , она составляет 97,16 (млн. руб.)

Для нахождения среднего квадратического отклонения (σ) составим Таблицу 4.

Таблица 4

Стоимости основных фондов предприятий, млн. руб.	Середина интервала xi	Число предприятий fi	Накопленные (кумулятивные) частоты	_  │xi - x│	_ │xi - x│*f i	_ 2 │xi - x│*f i
70-77 77-84 84-91 91-98 98-105 105-112 112-119 119-126 126-133 133-140	73,5 80,5 87,5 94,5 101,5 108,5 115,5 122,5 129,5 136,5	4 6 8 9 7 9 4 2 0 1	4 10 18 27 34 43 47 49 49 50	23,66 16,66 9,66 2,66 4,34 11,34 18,34 25,34 32,34 39,34	94,64 99,96 77,28 23,94 30,38 102,06 73,36 50,68 0 39,34	2239,1824 1665,3336 746,5248 63,6804 131,8492 1157,3604 1345,4224 1284,2312 0 1547,6356
Всего		50		78,4	591,64	10181,22

10181,22

Итак , σ = √ ————— = 14,26970217 (млн. руб.)

50

Б) Определим коэффициент вариации (V)

Коэффициент вариации (V) рассчитывается по следующей формуле:

σ

V = — *100 %, следовательно

_

x

14,26970217

V = —————— *100% = 14,6868075 %

97,16

Округлив, получим V = 14,7 % ,т.к. коэффициент вариации (V) не превышает 33 %, мы можем сказать, что данная совокупность считается однородной.

В) Определим модальный интервал распределения и моду.

Модальный интервал распределения – это интервал с наиболее часто встречающимися показателями (имеющий наибольшую частоту). Исходя из данных задачи №1 таких интервалов два: а) 91-98(млн. руб.) и б) 105-112 (млн. руб.).

Мода (наиболее часто встречающееся значение, в нашем случае стоимость основных фондов предприятий) находится в двух интервалах а) 91-98(млн. руб.)

б) 105-112 (млн. руб.).

Определим Моду (Мо) по следующей формуле:

f 4 - f 3

Мо 1 = xн+h —————————— ,

( f 4 - f 3 ) + ( f 4 - f 5 )

где xн - нижняя граница модального интервала

f 6 - f 5

Мо 2 = xн+h ——————————— ,

( f 6 - f 5 ) + ( f 6 - f 7 )

где xн - нижняя граница модального интервала

9-8

Мо 1 = 91+7 —————— = 93,33 (млн. руб.).

(9-8 )+( 9-7)

9-7

Мо 2 = 105+7 —————— = 107 (млн. руб.).

(9-7)+( 9-4)

Ответ: А) среднее квадратическое отклонение σ = 14,26970217 (млн. руб.);

Б) коэффициент вариации V = 14,7 % ,т.к. коэффициент вариации (V) не превышает 33 %, следовательно, данная совокупность считается однородной;

В) модальных интервалов распределения два :а) 91-98(млн. руб.) и б) 105-112 (млн. руб.), мода Мо 1 = 93,33 (млн. руб.), Мо 2 = 107 (млн. руб.).

3.Выполнить задачу №2.

Задача № 2.

Имеются следующие данные о среднесписочной численности работников предприятия за 5 лет.

Таблица 5

Год	1998	1999	2000	2001	2002
Среднесписочная численность, чел. (Вариант 2)	74	77	79	84	81

Рассчитать:

1.         средний уровень численности работников предприятия за 5 лет;

2.         ежегодные абсолютные приросты, темпы роста и темпы прироста численности работников предприятия;

3.         среднегодовой темп роста численности работников предприятия.

Решение.

1.Расчитаем средний уровень численности работников предприятия за 5 лет. Он определяется как средняя арифметическая простая:

_ ∑ xi 74+77+79+84+81 395

x = ———— = ———————— = ——— =79 (человек)

 n 5  5