Навигация
Принцип учета влияния инфляции и риска, а также другие принципы
7. Принцип учета влияния инфляции и риска, а также другие принципы.
Все перечисленные принципы одинаково важны при оценке эффективности состоятельности проекта, однако наиболее важным, на наш взгляд, является принцип учета наличия разных участников проекта. Это связано с тем, что наиболее эффективным будет тот проект, который в большей степени будет отвечать интересам всех его участников.
§3. МЕТОДИКА АНАЛИЗА ЭКОНОМИЧЕСКОЙ ЭФФЕКТИВНОСТИ ИНВЕСТИЦИОННОГО ПРОЕКТА
В основе процесса принятия управленческих решений инвестиционного характера лежит оценка и сравнение объема предполагаемых инвестиций и будущих денежных поступлений. Общая логика анализа с использованием формализованных критериев в принципе достаточно очевидна - необходимо сравнивать величину требуемых инвестиций с прогнозируемыми доходами. Поскольку сравниваемые показатели относятся к различным моментам времени, ключевой проблемой здесь является их сопоставимость. Относиться к ней можно по-разному в зависимости от существующих объективных и субъективных условий: темпа инфляции, размера инвестиций и генерируемых поступлений, горизонта прогнозирования, уровня квалификации аналитика и т.п.
К критическим моментам в процессе оценки единичного проекта или составления бюджета капиталовложений относятся: а) прогнозирование объемов реализации с учетом возможного спроса на продукцию (поскольку большинство проектов связано с дополнительным выпуском продукции); б) оценка притока денежных средств по годам; в) оценка доступности требуемых источников финансирования; г) оценка приемлемого значения цены капитала, используемого в том числе и в качестве коэффициента дисконтирования.
Анализ возможной емкости рынка сбыта продукции, т.е. прогнозирование объема реализации, наиболее существен, поскольку его недооценка может привести к потере определенной доли рынка сбыта, а его переоценка - к неэффективному использованию введенных по проекту производственных мощностей, т.е. к неэффективности сделанных капиталовложений.
Что касается оценки притока денежных средств по годам, то основная проблема возникает в отношении последних лет реализации проекта, поскольку, чем дальше горизонт планирования, т.е. чем более протяжен во времени проект, тем более неопределенными и рискованными рассматриваются притоки денежных средств отдаленных лет. Поэтому могут выполняться несколько расчетов, в которых в отношении значений поступлений последних лет реализации проекта могут вводиться понижающие коэффициенты либо эти поступления ввиду существенной неопределенности могут вообще исключаться из анализа.
Как правило, компании имеют множество доступных к реализации проектов, и основным ограничителем является возможность их финансирования. Источники средств существенно варьируют по степени их доступности -наиболее доступны собственные средства, т.е. прибыль, далее по степени увеличения срока мобилизации следуют банковские кредиты, займы, новая эмиссия. Как уже отмечалось выше, эти источники различаются не только продолжительностью срока их вовлечения в инвестиционный процесс, но и ценой капитала, величина которой также зависит от многих факторов. Кроме того, цена капитала, привлекаемого для финансирования проекта, в ходе его реализации может меняться (как правило, в сторону увеличения) в силу разных обстоятельств. Это означает, что проект, принимаемый при одних условиях, может стать невыгодным при других. Различные проекты не одинаково реагируют на увеличение цены капитала. Так, проект, в котором основная часть притока денежных средств падает на первые годы его реализации, т.е. возмещение сделанных инвестиций осуществляется более интенсивно, в меньшей степени чувствителен к удорожанию цены за пользование источником средств.
. С формальной точки зрения любой инвестиционный проект зависит от ряда параметров, которые в процессе анализа подлежат оценке и нередко задаются в виде дискретного распределения, что позволяет проводить этот анализ в режиме имитационного моделирования. В наиболее общем виде инвестиционный проект Р представляет собой следующую модель:
Р = {/С,-, CFk, n, r}, (3.1)
где /С, - инвестиция в/-М году,/=1,2.....т (чаще всего считается, что т=1);
CFk- приток (отток) денежных средств в /с-м году, /с=1,2.....п;
п - продолжительность проекта;
г - коэффициент дисконтирования.
Инвестиционные проекты, анализируемые в процессе составления бюджета капиталовложений, имеют определенную логику.
• С каждым инвестиционным проектом принято связывать денежный поток, элементы которого представляют собой либо чистые оттоки, либо чистые притоки денежных средств; в данном случае под чистым оттоком денежных средств в k-м году понимается превышение текущих денежных расходов по проекту над текущими денежными поступлениями (соответственно, при обратном соотношении имеет место чистый приток); иногда в анализе используется не денежный поток, а последовательность прогнозных значений чистой годовой прибыли, генерируемой проектом.
• Чаще всего анализ ведется по годам, хотя это ограничение не является безусловным или обязательным; иными словами, анализ можно проводить по равным базовым периодам любой продолжительности (месяц, квартал, год, пятилетка и др.), необходимо лишь помнить об увязке величин элементов денежного потока, процентной ставки и длины этого периода.
• Предполагается что весь объем инвестиций делается в конце года, предшествующего первому году генерируемого проектом притока денежных средств, хотя в принципе инвестиции могут делаться в течение ряда последующих лет.
• Приток (отток) денежных средств имеет место в конце очередного года (подобная логика вполне понятна и оправданна, поскольку, например, именно так считается прибыль - нарастающим итогом на конец отчетного периода).
• Коэффициент дисконтирования, используемый для оценки проектов с помощью методов, основанных на дисконтированных оценках, должен соответствовать длине периода, заложенного в основу инвестиционного проекта (например, годовая ставка берется только в том случае, если длина периода - год).
Необходимо особо подчеркнуть, что применение методов оценки и анализа проектов предполагает множественность используемых прогнозных оценок и расчетов. Множественность определяется как возможностью применения ряда критериев, так и безусловной целесообразностью варьирования основными параметрами. Это достигается использованием имитационных моделей в среде электронных таблиц.
Критерии, используемые в анализе инвестиционной деятельности, можно подразделить на две группы в зависимости от того, учитывается или нет временной параметр: а) основанные на дисконтированных оценках; б) основанные на учетных оценках. К первой группе относятся критерии: чистый приведенный эффект (Net Present Value, NPV); индекс рентабельности инвестиции (Profitability Index, PI); внутренняя норма прибыли (Internal Rate of Return, IRR); модифицированная внутренняя норма прибыли (Modified Internal Rate of Return, MIRR); дисконтированный срок окупаемости инвестиции (Discounted Payback Period, DPP). Ко второй группе относятся критерии: срок окупаемости инвестиции (Payback Period, PP); коэффициент эффективности инвестиции (Accounting Rate of Return, ARR). Рассмотрим ключевые идеи, лежащие в основе методов оценки инвестиционных проектов, использующих данные критерии.
3.1. Метод расчета чистого приведенного эффектаВ основе данного метода заложено следование основной целевой установке, определяемой собственниками компании - повышение ценности фирмы, количественной оценкой которой служит ее рыночная стоимость. Тем не менее принятие решений по инвестиционным проектам чаще всего инициируется и осуществляется не собственниками компании, а ее управленческим персоналом. Поэтому здесь молчаливо предполагается, что цели собственников и высшего управленческого персонала конгруэнтны , т.е. негативные последствия возможного агентского конфликта не учитываются.
Этот метод основан на сопоставлении величины исходной инвестиции (1C) с общей суммой дисконтированных чистых денежных поступлений, генерируемых ею в течение прогнозируемого срока. Поскольку приток денежных средств распределен во времени, он дисконтируется с помощью коэффициента г, устанавливаемого аналитиком (инвестором) самостоятельно исходя из ежегодного процента возврата, который он хочет или может иметь на инвестируемый им капитал.
Допустим, делается прогноз, что инвестиция (1C) будет генерировать в течение п лет годовые доходы в размере Р1, Р2, … , Рn- Общая накопленная величина дисконтированных доходов (Present Value, PV) и чистый приведенный эффект (Net Present Value, NPV) соответственно рассчитываются по формулам:
PV=å Pk /(1+r)^k (3.2)
NPV =å Pk /(1+r)^k-IC (3.3)
Очевидно, что если: NPV > О, то проект следует
принять; NPV < 0, то проект следует отвергнуть;
NPV = О, то проект ни прибыльный, ни убыточный.
Имея в виду упомянутую выше основную целевую установку, на достижение которой направлена деятельность любой компании, можно дать экономическую интерпретацию трактовки критерия NPV с позиции ее владельцев, которая по сути и определяет логику критерия NPV:
• если NPV < 0, то в случае принятия проекта ценность компании уменьшится, т.е. владельцы компании понесут убыток;
• если NPV = 0, то в случае принятия проекта ценность компании не изменится, т.е. благосостояние ее владельцев останется на прежнем уровне;
• если NPV > 0, то в случае принятия проекта ценность компании, а следовательно, и благосостояние ее владельцев увеличатся.
Следует особо прокомментировать ситуацию, когда NPV = 0. В этом случае действительно благосостояние владельцев компании не меняется, однако, как уже отмечалось выше, инвестиционные проекты нередко принимаются управленческим персоналом самостоятельно, при этом менеджеры могут руководствоваться и своими предпочтениями. Проект с NPV = 0 имеет все же дополнительный аргумент в свою пользу - в случае реализации проекта благосостояние владельцев компании не изменится, но в то же время объемы производства возрастут, т.е. компания увеличится в масштабах. Поскольку нередко увеличение размеров компании рассматривается как положительная тенденция (например, с позиции менеджеров аргументация такова: в крупной компании более престижно работать, кроме того, и жалованье нередко выше), проект все же принимается.
При прогнозировании доходов по годам необходимо по возможности учитывать все виды поступлений как производственного, так и непроизводственного характера, которые могут быть ассоциированы с данным проектом. Так, если по окончании периода реализации проекта планируется поступление средств в виде ликвидационной стоимости оборудования или высвобождения части оборотных средств, они должны быть учтены как доходы соответствующих периодов.
Если проект предполагает не разовую инвестицию, а последовательное инвестирование финансовых ресурсов в течение т лет, то формула для расчета NPV модифицируется следующим образом:
NPV= å Pk /(1+r)^k- å ICj /(1+i)^j
(3.4)
где i - прогнозируемый средний уровень инфляции.
Расчет с помощью приведенных формул вручную достаточно трудоемок, поэтому для удобства применения этого и других методов, основанных на дисконтированных оценках, разработаны специальные финансовые таблицы, в которых табулированы значения сложных процентов, дисконтирующих множителей, дисконтированного значения денежной единицы и т. п. в зависимости от временного интервала и значения коэффициента дисконтирования.
При расчете NPV, как правило, используется постоянная ставка дисконтирования, однако при некоторых обстоятельствах, например, ожидается изменение уровня учетных ставок, могут использоваться индивидуализированные по годам коэффициенты дисконтирования. Если в ходе имитационных расчетов приходится применять различные коэффициенты дисконтирования, то, во-первых, формула (3.3) неприменима и, во-вторых, проект, приемлемый при постоянной дисконтной ставке, может стать неприемлемым.
Необходимо отметить, что показатель NPV отражает прогнозную оценку изменения экономического потенциала коммерческой организации в случае принятия рассматриваемого проекта. Этот показатель аддитивен в пространственно-временном аспекте, т.е. NPV различных проектов можно суммировать. Это очень важное свойство, выделяющее этот критерий из всех остальных и позволяющее использовать его в качестве основного при анализе оптимальности инвестиционного портфеля.
3.2. Метод расчета индекса рентабельности инвестицииЭтот метод является по сути следствием предыдущего. Индекс рентабельности (PI) рассчитывается по формуле
Pi=å Pk /(1+r)^k: IC.
(3.5)
Очевидно, что если: PI > 1, то проект следует принять,
PI < 1, то проект следует отвергнуть,
PI = 1, то проект не является ни прибыльным, ни убыточным.
В отличие от чистого приведенного эффекта индекс рентабельности является относительным показателем: он характеризует уровень доходов на единицу затрат, т.е. эффективность вложений - чем больше значение этого показателя, тем выше отдача каждого рубля, инвестированного в данный проект. Благодаря этому критерий PI очень удобен при выборе одного проекта из ряда альтернативных, имеющих примерно одинаковые значения NPV (в частности, если два проекта имеют одинаковые значения NPV, но разные объемы требуемых инвестиций, то очевидно, что выгоднее тот из них, который обеспечивает большую эффективность вложений), либо при комплектовании портфеля инвестиций с целью максимизации суммарного значения NPV.
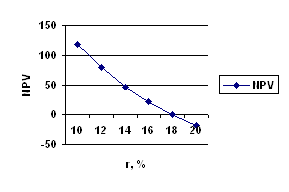
3.3. Метод расчета внутренней нормы прибыли инвестицииПод внутренней нормой прибыли инвестиции (IRR-синонимы: внутренняя доходность, внутренняя окупаемость) понимают значение коэффициента дисконтирования л, при котором NPV проекта равен нулю:
IRR = r, при котором NPV = f(r) = 0.
Иными словами, если обозначить IC = CF0, то IRR находится из уравнения:
å CFk /(1+IRR)^k=0
(3.6)
Смысл расчета внутренней нормы прибыли при анализе эффективности планируемых инвестиций, как правило, заключается в следующем: IRR показывает ожидаемую доходность проекта, и, следовательно, максимально допустимый относительный уровень расходов, которые могут быть ассоциированы с данным проектом . Например, если проект полностью финансируется за счет ссуды коммерческого банка, то значение 1RR показывает верхнюю границу допустимого уровня банковской процентной ставки, превышение которого делает проект убыточным.
На практике любая коммерческая организация финансирует свою деятельность, в том числе и инвестиционную, из различных источников. В качестве платы за пользование авансированными в деятельность организации финансовыми ресурсами она уплачивает проценты, дивиденды, вознаграждения и т.п., иными словами, несет некоторые обоснованные расходы на поддержание экономического потенциала. Показатель, характеризующий относительный уровень этих расходов в отношении долгосрочных источников средств, как обсуждалось выше, называется средневзвешенной ценой капитала (WACC). Этот показатель отражает сложившийся в коммерческой организации минимум возврата на вложенный в ее деятельность капитал, его рентабельность, и рассчитывается по формуле средней арифметической взвешенной.
Таким образом, экономический смысл критерия IRR заключается в следующем: коммерческая организация может принимать любые решения инвестиционного характера, уровень рентабельности которых не ниже текущего значения показателя "цена капитала" СС, под последним понимается либо WACC, если источник средств точно не идентифицирован, либо цена целевого источника, если таковой имеется. Именно с показателем СС сравнивается критерий IRR, рассчитанный для конкретного проекта, при этом связь между ними такова.
Данное утверждение верно лишь для "классического" проекта в том смысле, в каком он был определен ранее в данном разделе. Ниже будут приведены примеры проектов, для которых суждения о соотношении цены источника и IRR имеют другую интерпретацию.
Если: IRR > СС, то проект следует принять; IRR < СС, то проект следует отвергнуть; IRR = СС, то проект не является ни прибыльным, ни убыточным.
Независимо от того, с чем сравнивается IRR, очевидно одно: проект принимается, если его IRR больше некоторой пороговой величины; поэтому при прочих равных условиях, как правило, большее значение IRR считается предпочтительным.
Практическое применение данного метода осложнено, если в распоряжении аналитика нет специализированного финансового калькулятора. В этом случае применяется метод последовательных итераций с использованием табулированных значений дисконтирующих множителей. Для этого с помощью таблиц выбираются два значения коэффициента дисконтирования r-f < г2 таким образом, чтобы в интервале (r-i, г2) функция NPV = f(r) меняла свое значение с "+" на "-" или с "-" на "+". Далее применяют формулу
IRR=r1+f(r1)/(f(r1)-f(r2))*(r2-r1)
(3.8)
где r1 - значение табулированного коэффициента дисконтирования, при котором f(r1) > 0 (f(r1) < 0);
г2 - значение табулированного коэффициента дисконтирования, при котором f(r1) < 0 (f(r1) > 0).
Точность вычислений обратно пропорциональна длине интервала (r1, r2), а наилучшая аппроксимация с использованием табулированных значений достигается в случае, когда длина интервала минимальна (равна 1%), т.е. r1 и r2 - ближайшие друг к другу значения коэффициента дисконтирования, удовлетворяющие условиям (в случае изменения знака функции у = f(r) с "+" на "-"):
R1 - значение табулированного коэффициента дисконтирования, минимизирующее положительное значение показателя NPV, т.е. f(rj) = min {f(r) > 0};
г2 - значение табулированного коэффициента дисконтирования, максимизирующее отрицательное значение показателя NPV, т.е. f(r2) = max (f(r) < 0}.
Путем взаимной замены коэффициентов r1 и r2 аналогичные условия выписываются для ситуации, когда функция меняет знак с "-" на "+".
Пример
Требуется рассчитать значение показателя IRR для проекта, рассчитанного на три года, требующего инвестиций в размере 10 млн руб. и имеющего предполагаемые денежные поступления в размере 3 млн руб., 4 млн руб., 7 млн руб.
Возьмем два произвольных значения коэффициента дисконтирования: r = 10%, r = 20%. Соответствующие расчеты с использованием табулированных значений приведены в табл. 3.1. Тогда значение IRR будет равно:
IRR= 16,6%.
Можно уточнить полученное значение. Допустим, что путем нескольких итераций мы определили ближайшие целые значения коэффициента дисконтирования, при которых NPV меняет знак:
при r=16% NPV=+0,05; при r=17% WPV=-0,14. Тогда уточненное значение /RR будет равно: 0,05
IRR= 16,26%.
Истинное значение показателя IRR равно 16,23%, т.е. метод последовательных итераций обеспечивает весьма высокую точность (отметим, что с практической точки зрения такая точность является излишней). Свод всех вычислений приведен в табл. 4.1.
Таблица 3.1 Исходные данные для расчета показателя IRR
| Год | Поток | Расчет 1 | Расчет 2 | Расчет 3 | Расчет 4 | ||||
| г=10% | PV | г=20% | PV | /•=16% | PV | г=17% | PV | ||
| 0-й | -10 | 1,000 | -10,00 | 1,000 | -10,00 | 1,000 | -10,00 | 1,000 | -10,00 |
| 1-й | 3 | 0,909 | 2,73 | 0,833 | 2,50 | 0,862 | 2,59 | 0,855 | 2,57 |
| 2-й | 4 | 0,826 | 3,30 | 0,694 | 2,78 | 0,743 | 2,97 | 0,731 | 2,92 |
| 3-й | 7 | 0,751 | 5,26 | 0,579 | 4,05 | 0,641 | 4,49 | 0,624 | 4,37 |
| 1,29 | -0,67 | 0,05 | -0,14 | ||||||
Рассмотренная методика приложима лишь к акционерным обществам. В организациях, не являющихся акционерными, некоторым аналогом показателя WACC является уровень издержек производства и обращения (дебетовый оборот счета 46 "Реализация") в процентах к общей сумме авансированного капитала (итог баланса-нетто).
3.4. Метод определения срока окупаемости инвестицийЭтот метод, являющийся одним из самых простых и широко распространенных в мировой учетно-аналитичес-кой практике, не предполагает временной упорядоченности денежных поступлений. Алгоритм расчета срока окупаемости (РР) зависит от равномерности распределения прогнозируемых доходов от инвестиции. Если доход распределен по годам равномерно, то срок окупаемости рассчитывается делением единовременных затрат на величину годового дохода, обусловленного ими. При получении дробного числа оно округляется в сторону увеличения до ближайшего целого. Если прибыль распределена неравномерно, то срок окупаемости рассчитывается прямым подсчетом числа лет, в течение которых инвестиция будет погашена кумулятивным доходом. Общая формула расчета показателя РР имеет вид:
РР = min n, при котором åPk > IC
(3.9)
Нередко показатель РР рассчитывается более точно, т.е. рассматривается и дробная часть года; при этом делается молчаливое предположение, что денежные потоки распределены равномерно в течение каждого года. Так, для проекта с денежным потоком (млн руб.): -100 40 40 40 30 20 значение показателя РР равно 3 годам, если расчет ведется с точностью до целого года, или 2,5 года в случае точного расчета.
Некоторые специалисты при расчете показателя РР все же рекомендуют учитывать временной аспект. В этом случае в расчет принимаются денежные потоки, дисконтированные по показателю WACC, а соответствующая формула для расчета дисконтированного срока окупаемости, DPP, имеет вид:
DPP - min n, при котором å Pk/(1+r)^k
(3.10)
Для удобства расчетов можно пользоваться дисконтирующим множителем FM2(r%,n). Очевидно, что в случае дисконтирования срок окупаемости увеличивается, т.е. всегда DPP > PP. Иными словами, проект, приемлемый по критерию РР, может оказаться неприемлемым по критерию DPP. Рассмотрим пример.
Прежде всего необходимо отметить, что в оценке инвестиционных проектов критерии РР и DPP могут использоваться двояко: а) проект принимается, если окупаемость имеет место; б) проект принимается только в том случае, если срок окупаемости не превышает установленного в компании некоторого лимита.
Пример
Компания рассматривает целесообразность принятия проекта с денежным потоком, приведенным во второй графе табл. 4.2. Цена капитала компании 14%. Как правило, проекты со сроком погашения, превышающим 4 года, не принимаются. Сделать анализ с помощью критериев обыкновенного и дисконтированного сроков окупаемости.
Таблица 3.2 Оценка приемлемости проекта по критериям РР и DPP
| Год | Денеж- | Дисконти- | Дисконти- | Кумулятивное | |
| ный | рующий | рованный | возмещение | ||
| поток | множитель | денежный | инвестиции для | ||
| (млн | при | поток | потока (млн руб.) | ||
| руб.) | 1*14% | (млн руб.) | исход- | дисконти- | |
| ного | рованного | ||||
| 0-й -130 1,000 -130,0 -130 | -130,0 | ||||
| 1-й 30 0,877 26,3 -100 | -103,7 | ||||
| 2-й 40 0,769 30,8 -60 | -72,9 | ||||
| 3-й 50 0,675 33,8 -10 | -39,1 | ||||
| 4-й 50 0,592 29,6 40 | -9,5 | ||||
| 5-й 20 0,519 10,4 60 | 0,9 | ||||
Из приведенных в таблице расчетов видно, что РР = 4 годам (при точном расчете РР = 3,25 года), a DPP = 5 годам (при точном расчете DPP = 4,9 года). Таким образом, если решение принимается на основе обыкновенного срока окупаемости, то проект приемлем, если используется критерий дисконтированного срока окупаемости, то проект скорее всего будет отвергнут.
Показатель срока окупаемости инвестиции очень прост в расчетах, вместе с тем он имеет ряд недостатков, которые необходимо учитывать в анализе.
Во-первых, он не учитывает влияние доходов последних периодов. В качестве примера рассмотрим два проекта с одинаковыми капитальными затратами (10 млн руб.), но различными прогнозируемыми годовыми доходами: по проекту А - 4,2 млн руб. в течение трех лет; по проекту В - 3,8 млн руб. в течение десяти лет. Оба эти проекта в течение первых трех лет обеспечивают окупаемость капитальных вложений, поэтому с позиции данного критерия они равноправны. Однако очевидно, что проект В гораздо более выгоден.
Во-вторых, поскольку этот метод основан на недисконтированных оценках, он не делает различия между проектами с одинаковой суммой кумулятивных доходов, но различным распределением ее по годам. Так, с позиции этого критерия проект А с годовыми доходами 40, 60, 20 млн руб. и проект В с годовыми доходами 20, 40, 60 млн руб. равноправны, хотя очевидно, что первый проект более предпочтителен, поскольку обеспечивает большую сумму доходов в первые два года; эти дополнительные средства могут быть пущены в оборот и в свою очередь принесут новые доходы.
В-третьих, данный метод не обладает свойством аддитивности. Рассмотрим следующий пример (табл. 3.3).
Таблица 4.3 Динамика денежных потоков
| Год | Денежные | потоки по проектам | |||
| А | В | С | А и С | В и С | |
| 0-й | -10 | -10 | -10 | -20 | -20 |
| 1-й | 0 | 10 | 0 | 0 | 10 |
| 2-й | 20 | 0 | 0 | 20 | 0 |
| 3-й | 5 | 15 | 15 | 20 | 30 |
| Период | 2 | 1 | 3 | 2 | 3 |
| окупаемости | |||||
Допустим, что проекты А и В являются взаимоисключающими, а проект С - независимым. Это означает, что если у коммерческой организации есть финансовые возможности, то она может выбрать не только какой-то один из представленных проектов, но и их комбинации, т.е. проекты А и С или проекты В и С. Если рассматривать каждый проект отдельно с применением показателя "период окупаемости", можно сделать вывод, что предпочтительным является проект В. Однако если рассматривать комбинации проектов, то следует предпочесть комбинацию из "худших" проектов А и С.
Существует ряд ситуаций, при которых применение метода, основанного на расчете срока окупаемости затрат, является целесообразным. В частности, это ситуация, когда руководство коммерческой организации в большей степени озабочено решением проблемы ликвидности, а не прибыльности проекта - главное, чтобы инвестиции окупились, и как можно скорее. Метод также хорош в ситуации, когда инвестиции сопряжены с высокой степенью риска, поэтому чем короче срок окупаемости, тем менее рискованным является проект. Такая ситуация характерна для отраслей или видов деятельности, которым присуща большая вероятность достаточно быстрых технологических изменений. Таким образом, в отличие от критериев NPV, IRR и Р/ критерий РР позволяет получить оценки, хотя и грубые, о ликвидности и рисковости проекта. Понятие ликвидности проекта здесь условно: считается, что из двух проектов более ликвиден тот, у которого меньше срок окупаемости. Что касается сравнительной оценки рисковости проектов с помощью критерия РР, то логика рассуждений такова: денежные поступления удаленных от начала реализации проекта лет трудно прогнозируемы, т.е. более рисковы по сравнению с поступлениями первых лет; поэтому из двух проектов менее рисков тот, у которого меньше срок окупаемости.
3.5. Метод расчета коэффициента эффективности инвестицииЭтот метод имеет две характерные черты: во-первых, он не предполагает дисконтирования показателей дохода; во-вторых, доход характеризуется показателем чистой прибыли PN (прибыль за минусом отчислений в бюджет). Алгоритм расчета исключительно прост, что и предопределяет широкое использование этого показателя на практике: коэффициент эффективности инвестиции, называемый также учетной нормой прибыли (ARR), рассчитывается делением среднегодовой прибыли PN на среднюю величину инвестиции (коэффициент берется в процентах). Средняя величина инвестиции находится делением исходной суммы капитальных вложений на два, если предполагается, что по истечении срока реализации анализируемого проекта все капитальные затраты будут списаны; если допускается наличие остаточной или ликвидационной стоимости (RV), то ее оценка должна быть учтена в расчетах. Иными словами, существуют различные алгоритмы исчисления показателя ARR, достаточно распространенным является следующий:
ARR =PN/1/2*(IC+RV)
(3.11)
Данный показатель чаще всего сравнивается с коэффициентом рентабельности авансированного капитала, рассчитываемого делением общей чистой прибыли коммерческой организации на общую сумму средств, авансированных в ее деятельность (итог среднего баланса-нетто). В принципе возможно и установление специального порогового значения, с которым будет сравниваться ARR, или даже их системы, дифференцированной по видам проектов, степени риска, центрам ответственности и др.
Метод, основанный на коэффициенте эффективности инвестиции, также имеет ряд существенных недостатков, обусловленных в основном тем, что он не учитывает временной компоненты денежных потоков. В частности, метод не делает различия между проектами с одинаковой суммой среднегодовой прибыли, но варьирующей суммой прибыли по годам, а также между проектами, имеющими одинаковую среднегодовую прибыль, но генерируемую в течение различного количества лет, и т.п.
§4.ОСОБЕННОСТИ ИСПОЛЬЗОВАНИЯ ОПИСАННЫХ МЕТОДОВ НА ПРИМЕРЕ оао «НОМОС»
Коммерческая организация рассматривает целесообразность приобретения новой технологической линии. Стоимость линии составляет 10 млн долл.; срок эксплуатации - 5 лет; износ на оборудование начисляется по методу прямолинейной амортизации, т.е. 20% годовых; ликвидационная стоимость оборудования будет достаточна для покрытия расходов, связанных с демонтажем линии. Выручка от реализации продукции прогнозируется по годам в следующих объемах (тыс. долл.): 6800, 7400, 8200, 8000, 6000. Текущие расходы по годам оцениваются следующим образом: 3400 тыс. долл. в первый год эксплуатации линии с последующим ежегодным ростом их на 3%. Ставка налога на прибыль составляет 30%. Сложившееся финансово-хозяйственное положение коммерческой организации таково, что коэффициент рентабельности авансированного капитала составлял 21-22%; цена авансированного капитала (WACC) - 19%. В соответствии со сложившейся практикой принятия решений в области инвестиционной политики руководство организации не считает целесообразным участвовать в проектах со сроком окупаемости более четырех лет. Целесообразен ли данный проект к реализации?
Оценка выполняется в три этапа: 1) расчет исходных показателей по годам; 2) расчет аналитических коэффициентов; 3) анализ коэффициентов.
Этап 1. Расчет исходных показателей по годам
| Годы | |||||
| 1-й | 2-й | 3-й | 4-й | 5-й | |
| Объем реализации Текущие расходы Износ Налогооблагаемая прибыль Налог на прибыль Чистая прибыль Чистые денежные поступления | 6800 3400 2000 | 7400 3502 2000 | 8200 3607 2000 | 8000 3715 2000 | 5000 3827 2000 |
| 1400 420 | 1898 569 | 2593 778 | 2285 686 | 173 52 | |
| 980 2980 | 1329 3329 | 1815 3815 | 1599 3599 | 121 2121 | |
Этап 2. Расчет аналитических коэффициентов
а) расчет чистого приведенного эффекта по формуле (3.3), r = 19%:
NPV = - 10000 + 2980-0,8403 + 3329-0,7062 +
3815-0,5934 + 3599-0,4987 + 2121-0,4191 =
= -198 тыс. .долл.;
б) расчет индекса рентабельности инвестиции по формуле (3.5):
PI = 0,98;
в) расчет внутренней нормы прибыли данного проекта по формуле (3.7):
IRR = 18,1%;
г) расчет срока окупаемости проекта по формуле (3.9): срок окупаемости 3 года, поскольку кумулятивная сумма чистых денежных поступлений за этот период (10124 тыс. долл.) превышает объем капитальных вложений.
д) расчет коэффициента эффективности проекта по формуле (3.11):
среднегодовая чистая прибыль равна 1168,8 тыс.
долл.,
среднегодовой объем капитальных вложений составил 5000 тыс. долл.,
коэффициент эффективности равен 23,3%.
Этап 3, Анализ коэффициентов
Приведенные расчеты показывают, что в зависимости от того, какой критерий эффективности выбран за основу в данной коммерческой организации, могут быть сделаны диаметрально противоположные выводы. Действительно, согласно критериям NPV, PI и /RR проект нужно отвергнуть; согласно двум другим критериям (срок окупаемости и коэффициент эффективности) - принять. В данном случае можно ориентироваться на какой-то один или несколько критериев, наиболее важных по мнению руководства коммерческой организации, либо принять во внимание дополнительные объективные и субъективные факторы.
§5.ПРОТИВОРЕЧИВОСТЬ КРИТЕРИЕВ ОЦЕНКИ
Приведенный выше пример показывает, что даже в отношении единичного проекта решение о его принятии не всегда очевидно, поскольку выбор нужного критерия может при определенных условиях помочь "обосновать" то или иное решение. Очевидно, что ситуация резко усложнится, если приходится оценивать несколько проектов, причем находящихся в различных отношениях взаимозависимости. В примере показано, что противоречия возникли между критериями различных групп - основанных на дисконтированных и не дисконтированных оценках, однако даже на интуитивном уровне можно предположить, что такие расхождения могут возникнуть и внутри группы однородных критериев.
Действительно, что касается критериев РР и ARR, то они являются абсолютно независимыми друг от друга, и поскольку в компании могут устанавливаться различные пороговые значения для данных критериев, возможность возникновения противоречия между ними совершенно не исключена. Например, если бы в предыдущем примере рентабельность авансированного капитала в последние годы в компании составляла не менее 25%, то проект был бы отвергнут и по критерию ARR,
Взаимосвязи между критериями, основанными на дисконтированных оценках, несколько более сложны. В частности, существенную роль играет то обстоятельство, идет ли речь о единичном проекте или инвестиционном портфеле, в котором могут быть как независимые, так и взаимоисключающие проекты. Единичный проект является частным случаем портфеля независимых проектов. В этом случае критерии NPV, PI и IRR дают одинаковые рекомендации по поводу принятия или игнорирования проекта. Иными словами, проект, приемлемый по одному из этих критериев, будет приемлем и по другим. Причина такого "единодушия" состоит в том, что между показателями NPV, PI, IRR, CC имеются очевидные взаимосвязи:
если NPV > 0, то одновременно IRR > СС и PI > 1; если NPV < 0, то одновременно IRR < СС и PI < 1; если NPV = 0, то одновременно IRR = СС и Р/ = 1.
Однако независимыми проектами не исчерпывается все многообразие доступных вариантов инвестирования средств. Весьма обыденной является ситуация, когда менеджеру необходимо сделать выбор из нескольких возможных для реализации инвестиционных проектов. Причины могут быть разными, в том числе и ограниченность доступных финансовых ресурсов, означающая, что некоторые из приемлемых в принципе проектов придется отвергнуть или, по крайней мере, отложить на будущее. Возможна и такая ситуация, когда величина источников средств и их доступность заранее точно не определены или меняются с течением времени. В этом случае требуется по крайней мере ранжировать проекты по степени приоритетности независимо от того, являются они независимыми или взаимоисключающими. Оказывается, что во всех приведенных ситуациях сделать однозначный вывод не всегда возможно. Каким же критерием при этом следует пользоваться? Для иллюстрации рассмотрим простой пример.
Пример
В табл. 5.1 приведены исходные данные и аналитические коэффициенты по нескольким альтернативным проектам. Требуется оценить целесообразность выбора одного из них, если финансирование выбранного проекта может быть осуществлено за счет ссуды банка под 12% годовых (для простоты расходами по выплате процентов можно пренебречь).
Таблица 5.1
Динамика денежных потоков (ты с. дол л.)
| Год | Денежные потоки | |||
| проект 1 | проект 2 | проект 3 | проект 4 | |
| 0-й | -1200 | -1200 | -1200 | -1200 |
| 1-й | 0 | 100 | 300 | 300 |
| 2-й | 100 | 300 | 450 | 900 |
| 3-й | 250 | 500 | 500 | 500 |
| 4-й | 1200 | 600 | 600 | 250 |
| 5-й | 1300 | 1300 | 700 | 100 |
| NPV | 557,9 | 603,3* | 561,0 | 356,8 |
| PI | 1,46 | 1,50* | 1,47 | 1,30 |
| IRR | 22,7% | 25,0% | 27,1%* | 25,3% |
| РР | 4 года | 4 года | 3 года | 2 года* |
| ARR | 55,0%* | 53,3% | 45,0% | 28,3% |
| Примечания: 1) звездочкой отмечено лучшее значение данного показателя; | ||||
| 2) при расчете показателя ARR средне- | ||||
| годовой доход уменьшен на величину | ||||
| амортизации. | ||||
Результаты выполненных расчетов подтверждают сделанный ранее вывод о том, что возможна различная упорядоченность проектов по приоритетности выбора в зависимости от используемого критерия. Для принятия окончательного решения необходимы дополнительные формальные или неформальные критерии.
Некоторые аргументы в пользу того или иного критерия приводились выше. Прежде всего необходимо еще раз подчеркнуть, методы, основанные на дисконтированных оценках, с теоретической точки зрения, являются более обоснованными, поскольку учитывают временную компоненту денежных потоков. Вместе с тем они относительно более трудоемки в вычислительном плане.
Таким образом, основной вывод состоит в том, что из всех рассмотренных критериев наиболее приемлемыми для принятия решений инвестиционного характера являются критерии NPV, IRR и PI. Несмотря на отмеченную взаимосвязь между этими показателями, при оценке альтернативных инвестиционных проектов проблема выбора критерия все же остается. Основная причина кроется в том, что NPV - абсолютный показатель, a PI и IRR - относительные.
Пример
Рассмотрим два альтернативных проекта А и В с исходными данными, приведенными в табл. 5.2.
Таблица 5.2 Анализ альтернативных проектов
| Проект | Исходные | Годовой | NPV из | IRR,% | PI |
| инвести- | доход в | расчета | |||
| ции | течение | 13% | |||
| (тыс. руб.) | четырех | (тыс. руб.) | |||
| лет | |||||
| (тыс. руб.) | |||||
| А -700000 +250000 +43618 16,0 1,06 | |||||
| В -100000 +40000 +18979 21,9 1,19 | |||||
| А- В -600000 +210000 +24639 15,0 1,04 | |||||
Если проекты А и В рассматриваются изолированно, то каждый из них должен быть одобрен, поскольку они удовлетворяют всем критериям. Однако если проекты являются альтернативными, то выбор не очевиден, так как проект А имеет выше значение NPV, зато проект В предпочтительнее по показателям /RR и PI.
При принятии решения можно руководствоваться следующими соображениями:
а) рекомендуется выбирать вариант с большим NPV, поскольку этот показатель характеризует возможный прирост экономического потенциала коммерческой организации (наращивание экономической мощи компании является одной из наиболее приоритетных целевых установок);
б) возможно также сделать расчет коэффициента /RR для приростных показателей капитальных вложений и доходов (последняя строка таблицы); при этом если /RR > СС, то приростные затраты оправданны, и целесообразно принять проект с большими капитальными вложениями.
Исследования, проведенные крупнейшими специалистами в области финансового менеджмента, показали, что в случае противоречия более предпочтительно использование критерия NPV. Основных аргументов в пользу этого критерия два:
• Л/РУдает вероятностную оценку прироста стоимости коммерческой организации в случае принятия проекта; критерий в полной мере отвечает основной цели деятельности управленческого персонала, которой, как отмечалось ранее, является наращивание экономического потенциала компании, точнее рыночной оценки капитала собственников;
• NPV обладает свойством аддитивности, что позволяет складывать значения показателя NPV по различным проектам и использовать агрегированную величину для оптимизации инвестиционного портфеля.
Рекомендация о предпочтительности критерия NPV высказывается в основном учеными, которые, формируя такое мнение, исходят из основной целевой установки, стоящей перед любой компанией - максимизация благосостояния ее владельцев. Тем не менее на практике данная рекомендация не является доминирующей. Так, согласно данным Бригхема и Гапенски менеджеры американских компаний предпочитают критерий IRR критерию NPV в соотношении 3:1. Высказывается и предположение, объясняющее эту ситуацию, - решения в области инвестиций легче принимать, основываясь на относительных, а не на абсолютных оценках.
Более того, и с позиции теории нельзя категорично утверждать, что критерий NPV всегда является абсолютно лучшим. В следующем параграфе будут рассмотрены ситуации и дана интерпретация некоторых примечательных особенностей критерия IRR.
§6.АНАЛИЗ ИНВЕСТИЦИОННЫХ ПРОЕКТОВ В УСЛОВИЯХ РИСКА
Анализ в условиях риска основывается на похожих идеях. Поскольку основными характеристиками инвестиционного проекта являются элементы денежного потока и коэффициент дисконтирования, учет риска осуществляется поправкой одного из этих параметров. Рассмотрим несколько наиболее распространенных подходов.
Имитационная модель учета риска
Первый подход связан с корректировкой денежного потока и последующим расчетом NPV для всех вариантов (имитационное моделирование, или анализ чувствительности). Методика анализа в этом случае такова:
• по каждому проекту строят три его возможных варианта развития: пессимистический, наиболее вероятный, оптимистический;
• по каждому из вариантов рассчитывается соответствующий NPV, т.е. получают три величины: NPVp, NPVm/, NPV0;
• для каждого проекта рассчитывается размах вариации NPV по формуле
R(NPV) = NPV0 - NPVp;
• из двух сравниваемых проектов тот считается более рисковым, у которого размах вариации NPV больше.
Пример
Провести анализ двух взаимоисключающих проек-тов А и В, имеющих одинаковую продолжительность реализации (5 лет). Проект А, как и проект В, имеет одинаковые ежегодные денежные поступления. Цена капитала составляет 10%. Исходные данные и результаты расчетов приведены ниже.
| Показатель | Проект А | Проект В |
| Инвестиция | 9,0 | 9,0 |
| Экспертная оценка среднего | ||
| годового поступления: | ||
| пессимистическая | 2,4 | 2,0 |
| наиболее вероятная | 3,0 | 3,5 |
| оптимистическая | 3,6 | 5,0 |
| Оценка NPV (расчет): | ||
| пессимистическая | 0,10 | -1,42 |
| наиболее вероятная | 2,37 | 4,27 |
| оптимистическая | 4,65 | 9,96 |
| Размах вариации NPV | 4,55 | 11,38 |
Таким образом, проект В "обещает" больший NPV, но в то же время он более рискован.
Существуют модификации рассмотренной методи-I ки, предусматривающие применение количественных вероятностных оценок. В этом случае методика может иметь вид:
• по каждому варианту рассчитывается пессимистическая, наиболее вероятная и оптимистическая оценки денежных поступлений и NPV;
• для каждого проекта значениям NPVp, NPVmh NPV0 присваиваются вероятности их осуществления;
• для каждого проекта рассчитывается вероятное значение NPV, взвешенное по присвоенным вероятностям, и среднее квадратическое отклонение от него;
• проект с большим значением среднего квадратического отклонения считается более рисковым.
Методика построения безрискового эквивалентного денежного потока
В основу данной методики, по сути являющейся: обобщением предыдущей, заложены некоторые концептуальные идеи, развитые в рамках теории полезности и теории игр. В частности, крупнейшие специалисты в этой сфере научных исследований Дж. фон Нейман и О. Моргенштерн показали, что принятие' решений, в том числе и в области инвестиций, с помощью критериев, основанных только на монетарных оценках, не является безусловно оптимальным - более предпочтительно использование специальных кри- j терпев, учитывающих ожидаемую полезность того или j иного события. Для того чтобы получить некоторое представление о концепции полезности, рассмотрим ситуацию.
Инвестору требуется сделать выбор одного из двух I альтернативных вариантов получения дохода (млн. руб.):
Вариант А
Годовой доход Вероятность
20 0,5
40 0,5
Вариант В
Годовой доход Вероятность
- 0,5
60 0,5
Оба варианта имеют одинаковый средний ожидаемый годовой доход:
Вариант А: ERA = 20-0,5 + 40-0,5 = 30 млн руб.
Вариант В: ERB - 0-0,5 + 60-0,5 = 30 млн руб.
Если с позиции ожидаемого дохода проекты равноправны, то с позиции риска между ними есть существенное различие: используя один из описанных в теории критериев оценки риска, например, размах вариации, можно сделать вывод, что проект В более рисковый, т.е. при равном ожидаемом доходе он менее предпочтителен. Это можно продемонстрировать и другим способом - с помощью аппарата теории полезности.
Предположим, что некий инвестор, пользуясь некоторыми количественными критериями, или на основе интуиции, предварительно отобрал проект А как более предпочтительный и теперь пытается понять, а не следует ли все же отказаться от А и принять В. Очевидно, что если будет сделан переход от А к В, то при неблагоприятном развитии событий инвестор получит нулевой доход, т.е. на 20 млн руб. меньше, чем при реализации проекта А; наоборот, в удачный год его доход может быть на 20 млн руб. больше. Итак, с вероятностью 50% инвестор может выиграть дополнительно 20 млн руб., но с той же вероятностью 50% он может проиграть ту же самую сумму. Так стоит ли делать переход от А к В? В рамках теории полезности показано, что каждому событию свойственна определенная полезность. Переход от А к В, как правило, не делается, поскольку полезность получения дополнительного дохода меньше полезности потери той же самой суммы.
Логика здесь достаточно очевидна. Предположим, что человек, едва сводивший концы с концами, вдруг получил тысячу долларов. Эта сумма будет иметь для него исключительную полезность, поскольку попросту не даст умереть с голоду. Получение второй тысячи уже будет иметь меньшую полезность, так как основные (базовые) потребности человека уже были удовлетворены за счет первой тысячи. Понятно, что и возможность потери первой тысячи в сравнении с равновеликой возможностью приобретения второй тысячи имеют для этого индивидуума совершенно разные последствия, а следовательно, и значение. Рассуждая далее по той же схеме, можно сделать вывод, что с каждым новым приростом дохода полезность этого события будет уменьшаться. Таким образом, по мере роста потребления дополнительная полезность его прироста снижается.
Эта концепция убывающей предельной полезности может быть продемонстрирована в приложении к нашему примеру следующим образом. Предположим, что предельная полезность получения первых 10 млн Руб. составляет 1; вторых 10 млн руб. - 0,9, третьих 10 млн руб. - 0,79 и т.д. Иными словами, темпы снижения образуют арифметическую прогрессию
ak = где а-, = 0,1; d - 0,01.
(k -
Тогда изменение дохода инвестора в терминах по- ; лезности будет иметь вид:
| Доход | Предельная полезность | Полезность |
| 0 | 0 | 0 |
| 10 | 1 | 1 |
| 20 | 0,9 | 1,9 |
| 30 | 0,79 | 2,69 |
| 40 | 0,67 | 3,36 |
| 50 | 0,54 | 3,90 |
| 60 | 0,40 | 4,30 |
Проекты А и В в терминах полезности имеют следующие характеристики:
| Вариант А | Вариант В | |||||
| Годовой доход | Вероятность | Полезность | Годовой доход | Вероятность | Полезность | |
| 20 40 | 0,5 0,5 | 1,9 3,36 | - 60 | 0,5 0,5 | 0 4,3 | |
| Ожидаемый доход Ожидаемая полезность | 30 2,63 | 30 2,15 | ||||
Примечание. Ожидаемые значения дохода и полезности представляют собой математические ожидания данных показателей, т.е. они найдены по формуле средней арифметической взвешенной, в которой весами выступают значения вероятностей.
Таким образом, если по критерию "ожидаемый доход" нельзя было сделать выбор между проектами, то по критерию "ожидаемая полезность" явное предпочтение отдается проекту А. Это в точности согласуется с ранее сделанным выводом об относительно большей рискованности проекта В по сравнению с проектом А.
Логика построения безрисковых эквивалентов в значительной степени базируется на идеях теории полезности в том смысле, что, рассматривая поэлементно денежный поток рискового проекта, инвестор в отношении его пытается оценить, какая гарантированная, т. е. безрисковая, сумма денег потребуется ему, чтобы быть индифферентным к выбору между этой суммой и ожидаемой, т.е. рисковой, величиной k-го элемента потока.
Как же на практике находят безрисковые эквиваленты? Существуют различные способы. Например, можно попытаться оценить вероятность появления заданной величины денежного поступления для каждого года и каждого проекта. После этого составляются новые проекты на основе откорректированных с помощью понижающих коэффициентов денежных потоков и для; них рассчитываются NPV (понижающий коэффициента представляет собой вероятность появления рассматриваемого денежного поступления). По сути, откорректированный поток и представляет собой поток из безрисковых эквивалентов. Предпочтение отдается проекту откорректированный денежный поток которого имеет наибольший NPV; этот проект считается менее рискованным.
С некоторой долей условности можно считать, что в теоретическом плане метод RADR более оправдан, поскольку введение поправки на риск автоматически приводит к принятию безусловно обоснованной предпосылки о возрастании риска с течением времени. Конечно, эта предпосылка может быть учтена и при расчете безрисковых эквивалентов. По свидетельству западных специалистов, из рассмотренных методов учета риска метод RADR пользуется большей популярностью. Обычно называют две причины: а) менеджеры и аналитики предпочитают работать с относительными показателями, в частности с показателями доходности; б) ввести поправку к коэффициенту дисконтирования гораздо легче, нежели рассчитывать безрисковые эквиваленты, тем более, что в любом случае решение является субъективным. Во многих компаниях для удобства вводят специальную шкалу, в которой указаны значения коэффициента дисконтирования в зависимости от того, какой уровень риска может быть приписан данному проекту, например: ниже среднего, средний, выше среднего и весьма высокий. Как градация шкалы, так и значения коэффициента дисконтирования периодически пересматриваются и, кроме joro, могут специфицироваться по видам инвестиций, подразделениям, регионам и другим классификационным признакам.
ЗАКЛЮЧЕНИЕ
Разработка, санкционирование и отбор конкретных вариантов капиталовложений обоснованно ставятся в один ряд с наиболее важными и сложными проблемами, изучение которых осуществляется в рамках финансового менеджмента (ФМ). Доказательством этому служит общепринятое подразделение прикладных задач ФМ на организационно-методические разработки и технологию реализации инвестиционных и финансовых решений. В основе процесса принятия оптимальных решений в области долгосрочного инвестирования лежат анализ, оценка и сравнение объема планируемых капиталовложений и ожидаемых результатов. Оптимизация инвестиционных решений — это процесс исследования множества факторов, воздействующих на ожидаемые результаты, в ходе которого менеджерами на основе ранее установленных критериев оптимизации осуществляется осознанный (рациональный) выбор наиболее эффективного варианта капиталовложений. В качестве критерия оптимизации в сравнительной оценке различных инвестиций будут выступать количественные показатели результативности долгосрочных инвестиционных проектов.
В современной научной литературе исследованию данной проблемы уделено немало внимания. Методические рекомендации зарубежных организаций (например, ЮНИДО), разработки отечественных ученых и государственных органов Российской Федерации нацелены на необходимость единообразного подхода к оценке различных инвестиционных проектов с учетом накопленного за последние годы отечественного и зарубежного опыта. Однако при всем многообразии распространенных в настоящее время методик инвестиционного анализа, недостаточно изученной остается проблема комплексного подхода в оценке многоцелевых коммерческих и некоммерческих установок долгосрочного инвестирования. Нечетко представлены отдельные положительные и отрицательные стороны каждого показателя, специфические условия и особенности его применения на практике.
Можно выделить следующие семь ключевых вопросов (список решений, которые должен принять финансовый менеджер), ответ на которые может быть получен в ходе использования основных положений комплексного анализа долгосрочных инвестиций (КАДИ):
по какому критерию оценивать инвестиционный проект (ИП);
принимать или не принимать участие в ИП на предложенных инвестором (коммерческим банком, инвестиционным фондом и пр.) условиях финансирования;
вкладывать или не вкладывать капитал в конкретный проект;
какой из нескольких альтернативных (взаимоисключающих) проектов предпочесть;
замещать или ремонтировать основные фонды (оборудование);
в какой период свертывать (ликвидировать) инвестиции;
какие проекты отобрать в портфель инвестиций.
Обоснование вышеперечисленных решений не может быть выполнено только с использованием одних результатов оценки эффективности ИП. Комплексный подход к изучению сложных экономических явлений предполагает исследование взаимосвязей и взаимозависимостей с другими разделами КАДИ. Другими словами, принятие рационального управленческого решения должно основываться на определенных критериях оценки, однако помимо этого в процессе принятия оптимальных инвестиционных решений необходимо учитывать результаты анализа риска, воздействия инфляции, расчеты цены и структуры капитала и пр.
Основополагающими принципами оценки эффективности долгосрочных инвестиций являются: моделирование потоков продукции, ресурсов и денежных средств по периодам реализации ИП; комплексный учет внешних и внутренних факторов реализации ИП; определение эффекта посредством сопоставления ожидаемых инвестиционных результатов и затрат; учет временной ценности денежных вложений и требуемой ставки рентабельности на инвестированный капитал. В ходе оценки ИП широко используются классические методы анализа (сравнения, балансовый, элиминирования, корреляционно-регрессионного анализа, графический, простых и сложных процентов, дисконтирования и пр.), а также такие распространенные конкретно-аналитические приемы исследования, как расчет абсолютных, относительных и средних величин, детализация показателей на его составляющие, сводки и группировки.
Для принятия оптимальных инвестиционных решений менеджерам необходимо комплексно изучить соответствующие показатели экономического эффекта и эффективности. В первом случае определяются абсолютные результативные показатели инвестиционной деятельности. В свою очередь, эффективность долгосрочных инвестиций характеризуется системой относительных показателей, соизмеряющих полученный эффект с затратами инвестированного в проект капитала. На практике принято различать показатели коммерческой (оценка финансовых последствий осуществления капиталовложений для непосредственных участников процесса долгосрочного инвестирования), бюджетной (оценка финансовых последствий реализации ИП для бюджетов различных уровней) и экономической эффективности долгосрочных инвестиций.
В основе классификации показателей проектной оценки лежит подразделение их на три главные группы: дисконтные, комплексные и показатели, при расчете которых не учитывается фактор времени. Обращая внимание на исходные положения анализа экономической целесообразности капиталовложений, нетрудно заметить, что принцип учета временной ценности денежных вложений и требуемой ставки рентабельности в основном реализуется в первой группе показателей, к которым относятся чистая текущая стоимость, внутренняя норма рентабельности, дисконтированный срок окупаемости, индекс рентабельности инвестиций и пр. Точность расчета данных показателей в значительной степени зависит от достоверности и объективности оценки соответствующих денежных потоков и проектной дисконтной ставки.
Однако, как показывает практика, многие компании по-прежнему предпочитают использовать в инвестиционном анализе сравнительно простые альтернативные показатели. Пренебрегая рекомендации ученых относительно теоретической обоснованности дисконтных показателей, финансовые менеджеры для оценки ИП рассчитывают максимум проектной прибыли, срок окупаемости, учетную норму рентабельности и пр.
Не все проекты могут иметь четко выраженные стоимостные результаты реализации, например, инвестиции в социальную сферу, экологию и безопасность труда. Если менеджерам удается субъективно оценить преимущества, которые фирма получит в ходе осуществления данных капиталовложений (как правило, точная стоимостная оценка объема
инвестиционных затрат не представляет трудностей для учетно-финан-совых работников), то для обоснования управленческих решений могут быть использованы традиционные количественные показатели, о которых упоминалось ранее. Более трудной процедурой является оценка долгосрочных инвестиций в некоммерческих организациях (в бюджетных учреждениях здравоохранения, образования и др.). В этом случае применяется так называемый СВА-подход (cost-benefit analysis). В его основе лежит сопоставление количественно измеримых затрат с множеством прямых и косвенных преимуществ (выгод). Последние являются комплексными показателями и должны учитывать относительную ценность ожидаемых результатов как для организации, так и для отдельных общественных групп с различными уровнями доходов. Применение на практике СВА-подхода сопряжено со значительными затратами на этапе разработки альтернативных вариантов капиталовложений. Это связано с необходимостью сбора и обработки обширного объема статистического материала, социологическими исследованиями, использованием высококвалифицированного персонала .
С теоретической точки зрения наиболее корректным среди формализованных показателей является чистая текущая стоимость проектных денежных потоков. Этот показатель представляет собой разницу между первоначальной величиной инвестиционных затрат (iQ) и общей суммой дисконтированных чистых денежных потоков за все периоды времени в течение планируемого срока реализации проекта. Высокая научная обоснованность принимаемых инвестиционных решений на основе показателя NPV связана не только с учетом фактора временной ценности денежных поступлений, генерируемых ИП в разных периодах времени. Успешная реализация проекта с положительной чистой текущей стоимостью фактически обеспечивает повышение рыночной цены обыкновенных акций фирмы. Тогда как известно из теории корпоративных финансов, что важнейшей целью функционирования компании в подавляющем большинстве случаев является максимизация благосостояния ее владельцев (SWM). На примере открытого акционерного общества показано, в какой степени инвестиционные решения, принятые на основе NPV-критерия, отвечают данной корпоративной цели.
Принимая за основу предпосылку о том, что инвестиции с положительной NPV будут приумножать благосостояние владельцев компании, а с отрицательной NPV — понижать его, можно сформулировать следующие правила принятия инвестиционных решений:
если результат NPV положительный, то можно осуществлять капиталовложения, если он отрицательный, то их следует отвергать;
если представленные проекты являются альтернативными
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1Бирман Г., Шмидт С. Экономический анализ инвестиционных проектов: Пер. с англ. / Под ред. Л.П.Белых. — М.: Банки и биржи, ЮНИТИ,485 с. 2002.
2. Бригхем Ю., Гапенски Л. Финансовый менеджмент: Полный курс. В 2-х т.: Пер. с англ. / Под ред. В.В.Ковалева. - СПб: Экономическая школа,238 с. 2001.
3. Ван Хорн Дж. Основы управления финансами: Пер. с англ. / Под ред. И. И. Елисеевой. - М.: Финансы и статистика,634 с. 2001.
4. Гальперин В.М., Игнатьев С.М., Моргунов В.И. Микроэкономика. - Т. 1. - СПб: Экономическая школа,267 с. 2002.
5. Друри К. Введение в управленческий и производственный учет: Пер. с англ. / Под ред. С.А.Табалиной. - М.: Аудит, ЮНИТИ,438 с. 2002.
6. Инвестиционно-финансовый портфель(Книга инвестиционного менеджера. Книга финансового менеджера. Книга финансового посредника). / Отв. ред. Рубин Ю.Б., Солдат-кин В.И. - М.:"СОМИНТЭК", 282 с.2002.
7. Ковалев 6.6. Финансовый анализ: Управление капиталом. Выбор инвестиций. Анализ отчетности. - 2-е изд., пе-рераб. и доп. - М.: Финансы и статистика,322 с. 2002.
8. Липсиц И.В., Коссов Б.Б. Инвестиционный проект: методы подготовки и анализа: Учебно-справочное пособие. - М.: Издательство БЕК,189 с. 2000.
9. Нейман Дж. фон, Моргенштерн О. Теория игр и экономическое поведение. — М.,293 с. 1999.
10. Райфа Г. Анализ решений. - М.,148 с. 2002.
11. Справочник финансиста предприятия. — М.: ИНФРА-М,365 с. 2002.
12. Финансовое управление компанией / Общ. ред. Е. В.Кузнецовой. - М.: Фонд "Правовая культура",392 с. 2002.
13. Фридман Д., Ордуэй Н. Анализ и оценка приносящей доход недвижимости: Пер. с англ. - М.: "Дело Лтд",758 с.2002.
14. Хендриксен Е.С., Ван Бреда М.Ф. Теория управленческого учета: Пер. с англ. / Под ред. Я. В. Соколова. - М.: Финансы и статистика,141, 2002.
15. Четыркин Е.М. Методы финансовых и коммерческих расчетов. - 2-е изд., испр. и доп. - М.: "Дело Лтд", 218 с.2002
16. Шарп У.Ф., Александер Г.Дж., БейлиДж. Инвестиции-Пер. с англ. - М.: ИНФРА-М,288 с. 2002.
17. BrealeyRA., Myers S.C. Principles of Corporate Finance 4-th ed. - McGraw Hill, Inc., 480 p. 2001.
Похожие работы
... рисков, нестабильности экономики, сложности прогнозирования денежных потоков и т.д. Поэтому эффективность инвестиционных проектов следует оценивать по нескольким критериям и нескольким методам [ 33, с.280]. 2 Экономическая оценка реализации проекта по производству полиэтилена 2.1 Перспективы развития полиэтилена в России Полиэтилен различных марок (LLDPE, LDРЕ, НDРЕ) на мировых рынках ...
... денежных потоков в год (15% на все 10 млрд. руб. инвестиций), т. е. использоваться с рентабельностью не менее 18,75%. Глава 3. Методы оценки эффективности инвестиционных проектов. 3.1 Российский опыт оценки эффективности инвестиционных проектов. В период плановой экономики действовала официально утвержденная методика определения экономической эффективности капитальных вложений. Согласно ей ...
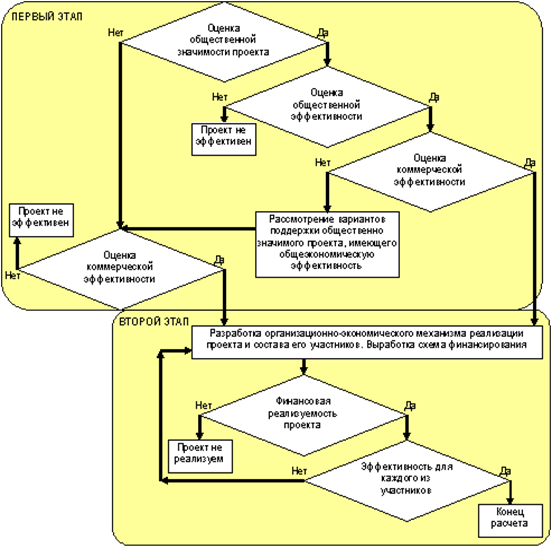
тся главной, определяющей судьбу проекта в целом. Схема 1. Концептуальная схема оценки эффективности инвестиционного проекта. Первый этап. Эффективность проекта в целом. На первом этапе рассчитываются показатели эффективности проекта в целом. Цель этого этапа - агрегированная экономическая оценка проектных решений и создание необходимых условий для поиска инвесторов. 1.1 Оценка ...
... будет превышать таковую для любого иного способа вложения капитала. Итак, проблема оценки привлекательности инвестиционного проекта заключается в определении уровня его доходности (нормы прибыли). Различают два основных подхода к решению данной проблемы, в соответствии с которыми и методы оценки эффективности инвестиций предлагается разделить на две группы: 1) простые (статические) методы; 2) ...
0 комментариев