Навигация
Решить задачу, используя критерий Розенбаума
9. Решить задачу, используя критерий Розенбаума.
Экспериментатор измерил, используя тест Векслера, показатели интеллекта у двух групп респондентов из городской и сельской местности. Его интересует вопрос – будут ли обнаружены статистические значимые различия в показателях интеллекта. В городской группе было 11 человек, в сельской – 12.
| город | 96 | 100 | 104 | 104 | 120 | 120 | 120 | 120 | 126 | 130 | 134 | |
| село | 76 | 82 | 82 | 84 | 88 | 96 | 100 | 102 | Ё04 | 110 | 118 | 120 |
Решение
Таблица 1.
Индивидуальные значения вербального интеллекта в выборках городских (n1=11) и сельских (n2=12) респондентов
| Город | Показатель вербального интеллекта | Село | Показатель вербального интеллекта | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Упорядочим значения в обеих выборках, а затем сформулируем гипотезы:
H0: горожане не превосходят сельчан по уровню вербального интеллекта.
H1: горожане превосходят сельчан по уровню вербального интеллекта.
Таблица 2
Упорядоченные по убыванию вербального интеллекта ряды индивидуальных значений в двух выборках
| 1 ряд – горожане | 2 ряд – сельчане | ||||||||||||||||||||||||
|
| ||||||||||||||||||||||||
Как видно из табл. 2, мы правильно обозначили ряды: первый тот, что "выше" - ряд горожан, а второй, тот, что "ниже” - ряд сельчан. По табл. 2. определяем количество значений первого ряда, которые больше максимального значения второго ряда: S1=3. Теперь определяем количество значений второго ряда, которые меньше минимального значения первого ряда: S2=5. Вычисляем по формуле:
Qэмп =S1+S2=3 + 5 =8
По табл.1 Приложения 1 определяем критические значения Q для n1=11, n2=12;
| Правило отклонения Н0 в принятия Н1 Если эмпирическое значение критерия равняется критическому значению,cответствующему р≤0,05 или превышает его, то Н0 отклоняется, но мы еще не можем определенно принять Н1. Если эмпирическое значение критерия равняется критическому значению, соответствующему р≤0,01 или превышает его, то Н0 отклоняется и принимаетсяH1. |
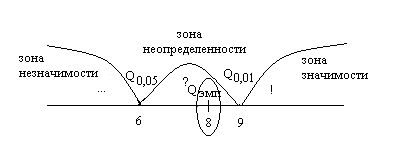
Рис 1. ось значимости для критерии Q Разенбаума
Эмпирическое значение критерия попадает в область между Q0,05 и Q0,01. Это зона "неопределенности": мы уже можем отклонить гипотезу о недостоверности различий (Н0), но еще не можем принять гипотезы об их достоверности (H1).
Ответ: мы уже можем отклонить гипотезу о недостоверности различий интеллекта между городскими и сельскими жителями(Н0), но еще не можем принять гипотезы об их достоверности (H1).
10. Как рассчитать коэффициент корреляции Спримена, если мы имеем одинаковые ранги?
Поскольку в обоих сопоставляемых ранговых рядах присутствуют группы одинаковых рангов, перед подсчетом коэффициента ранговой корреляции необходимо внести поправки на одинаковые ранги Та и Тb:
Та=∑(а3-а)/12
Тb=∑(b3-b)/12
где a - объем каждой группы одинаковых рангов в ранговом ряду А,
b - объем каждой группы одинаковых рангов в ранговом ряду В.
Для подсчета эмпирического значения гs используем формулу:
rs=1-6![]()
При больших количествах одинаковых рангов изменения rs могут оказаться гораздо более существенными. Наличие одинаковых рангов означает меньшую степень днфферентдкрованностк упорядоченных переменных и, следовательно, меньшую возможность оценить степень связи между ними.
[1] Определения и формулы расчета М и σ даны в параграфе «Распределение признака. Параметры распределения».
Похожие работы
... , и , то можно предположить о правильном распределении объектов и уже существующих двух классах и верно выполненной классификации объектов подмножества М0. 3.2 Пример решения задачи дискриминантным анализом в системе STATISTICA Исходя из данных по 10 странам (рис. 3.1), которые были выбраны и отнесены к соответствующим группам экспертным методом (по уровню медицинского обслуживания), ...
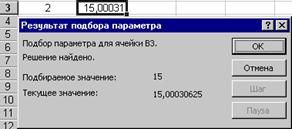
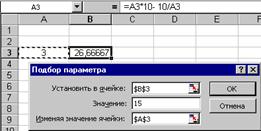
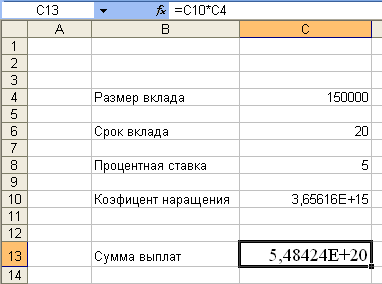
... ) или неположительным (второе решение). Задачу поиска параметра при налагаемых граничных условиях поможет решить специальная надстройка Microsoft Excel Поиск решения. 2 Практическая часть 2.1 Пример решения задач с использованием функции “подбор параметра” Как известно, формулы в Microsoft Excel позволяют определить значение функции по ее аргументам. Однако может возникнуть ситуация, ...
... его увеличением для целей информационного обеспечения исполнительных местных органов [7,8]. 3 ОПЫТ УПРАВЛЕНИЯ И ОБОЩЕНИЕ ДАННЫХ НА ПРИМЕРЕ АЛМАТИНСКОГО ОБЛАСТНОГО УПРАВЛЕНИЯ СТАТИСТИКИ3.1 Алматинское областное управление статистики как субъект сбора и обобщения статистической информации В своей деятельности Алматинское областное управление статистики (АОУС) руководствуется ...
... проверить знания студента из первой части курса, которая излагается в первых четырёх модулях. Во вторых вопросах билета проверяются знания классической предельной проблемы теории вероятностей и математической статистики, которые излагаются в следующих пяти модулях. 1. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: испытания с равновозможными исходами. 2. ...


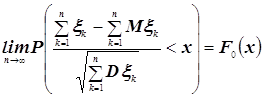
0 комментариев