Навигация
Применение средневзвешенных индексов в статистике
4. Применение средневзвешенных индексов в статистике
На примерах можно было увидеть, что общий агрегатный индекс одновременно является индексом средним из индивидуальных. Всякий общий агрегатный индекс можно исчислить как среднюю взвешенную величину из индивидуальных индексов. Но при таком способе расчета нужно правильно взять форму средней и систему весов для индивидуальных индексов. Вопрос о выборе формы средней и системы весов в этом случае решается на основе общего правила, что агрегатный индекс _ основная форма всякого экономического индекса. Следствием этого правила является то, что средний из индивидуальных индексов должен быть тождествен исходному агрегатному. Это означает, что средние из индивидуальных индексов выступают как преобразованная форма агрегатного индекса. А так как агрегатный индекс может быть преобразован только либо в средний арифметический, либо в средний гармонический, то, следовательно, при исчислении средних индексов могут быть использованы только две формы средних: средняя арифметическая и средняя гармоническая. Никакая другая форма при расчете не применяется.
Покажем преобразование агрегатного индекса качественного показателя в средний гармонический и средний арифметический на примере индекса цен.
В тех случаях, когда неизвестны отдельные значения ![]() и
и ![]() , но дано их произведение
, но дано их произведение ![]() , (товарооборот текущего периода) и индивидуальные индексы цен
, (товарооборот текущего периода) и индивидуальные индексы цен 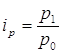 , а сводный индекс должен быть исчислен с отчетными весами, - применяется средний гармонический индекс цен. Причем, индивидуальные индексы должны быть взвешены таким образом, чтобы средний гармонический индекс совпал с агрегатным. Из формулы
, а сводный индекс должен быть исчислен с отчетными весами, - применяется средний гармонический индекс цен. Причем, индивидуальные индексы должны быть взвешены таким образом, чтобы средний гармонический индекс совпал с агрегатным. Из формулы 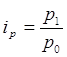 определяем неизвестное значение
определяем неизвестное значение  , подставляем его в знаменатель агрегатной формулы (9) и получаем средний гармонический индекс цен, который тождественен формуле Паше:
, подставляем его в знаменатель агрегатной формулы (9) и получаем средний гармонический индекс цен, который тождественен формуле Паше:
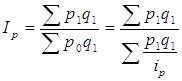 (13)
(13)
Весами индивидуальных индексов ![]() в этом индексе служит стоимость отдельных видов продукции отчетного периода в ценах того же периода
в этом индексе служит стоимость отдельных видов продукции отчетного периода в ценах того же периода ![]() .
.
Если из индивидуального индекса цен 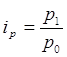 выразим цену отчетного периода
выразим цену отчетного периода ![]() и подставим в числитель агрегатного индекса цен (10), то получим средний арифметический индекс цен, тождественный агрегатному индексу Ласпейреса:
и подставим в числитель агрегатного индекса цен (10), то получим средний арифметический индекс цен, тождественный агрегатному индексу Ласпейреса:
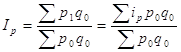
Весами осредняемых индивидуальных индексов в этом индексе служит объем товарооборота в базисном периоде (![]() ).
).
Аналогично индексу цен исчисляются и средние индексы себестоимости продукции.
Приведем общую схему преобразования агрегатных индексов в индексы средние арифметические и средние гармонические.
Таблица 1
| Наименование индекса | Индивидуальный индекс | Преобразование индивидуального индекса | Агрегатный индекс | Средний арифметический | Средний гармонический |
| Физического объема |
|
|
|
|
|
| Цен |
|
|
|
|
|
| Себестоимости |
|
|
|
|
|
| Производительности труда |
|
|
|
|
|
* Эти формулы теоретически возможны, практически они не применяются (см. список лит-ры п.5)
Важной особенностью общих индексов, построение и расчет которых составляют суть индексного метода, является то, что они обладают синтетическими и аналитическими свойствами:
Ø Синтетические свойства общих индексов состоят в том, что они выражают относительные изменения сложных (разнотоварных) явлений, отдельные части и элементы которых непосредственно несоизмеримы.
Ø Аналитические свойства общих индексов состоят в том, что посредством индексного метода определяется влияние факторов на изменение изучаемого показателя.
Таким образом, общие индексы являются синтетическими и аналитическими показателями, играющими важную роль в социально-экономических исследованиях.
II. Расчетная часть. Задание 25
Задача №1
Розничный товарооборот по трем районам характеризуется следующими данными:
| Район | Товарооборот в отчетном году, млн. руб. | Индексы товарооборота в отчетном году по сравнению с базисным | |
| В фактических ценах, число раз | В сопоставимых ценах, % | ||
| 1 | 2040 | 1,26 | 105 |
| 2 | 1500 | 1,20 | 80 |
| 3 | 2492 | 1,19 | 85 |
Определите:
1) среднее изменение цен на товары по каждому району;
2) общий индекс цен по трем районам;
3) общий индекс товарооборота в фактический ценах;
4) абсолютный прирост товарооборота вследствие изменения цен, объема продажи по каждому району и в целом по трем районам.
Решение:
Таблица 2
|
|
|
|
|
|
|
|
|
| |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 2040 | 1,26 | 1,05 | 1,2 | 1700 | 1619 | 340 | 81 | 421 |
| 2 | 1500 | 1,2 | 0,8 | 1,5 | 1000 | 1250 | 500 | -250 | 250 |
| 3 | 2492 | 1,19 | 0,85 | 1,4 | 1780 | 2094 | 712 | -314 | 398 |
|
| 6032 | 4480 | 4963 | 1552 | -483 | 1069 |
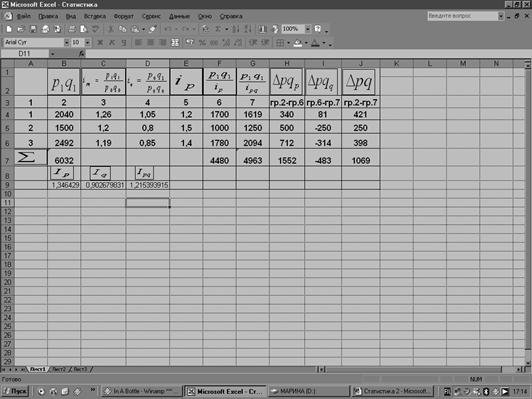
Таблица 3.
1) Для того, чтобы узнать среднее изменение цен на товары по каждому району произведем вычисления по следующей формуле:
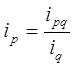 (см. гр.5 табл.2)
(см. гр.5 табл.2)
а) ![]() ; Среднее повышение цен на товары в первом районе составило 20% (120-100).
; Среднее повышение цен на товары в первом районе составило 20% (120-100).
б) ![]() ; Среднее повышение цен на товары во втором районе составило 50%.
; Среднее повышение цен на товары во втором районе составило 50%.
в) ![]() ; Среднее повышение цен на товары в третьем районе составило 40%.
; Среднее повышение цен на товары в третьем районе составило 40%.
2) Определим общий индекс цен по трем районам по формуле среднего взвешенного гармонического индекса.
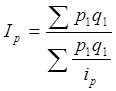 .
.
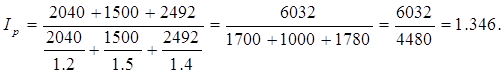 или 134,6%. Среднее повышение цен в общем по трем районам составило 34,6%.
или 134,6%. Среднее повышение цен в общем по трем районам составило 34,6%.
3) Найдем общий индекс физического объема товарооборота.
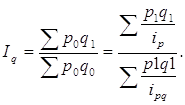
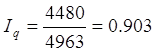 или 90,3%. Среднее снижение физического объема товарооборота составило 9,7%
или 90,3%. Среднее снижение физического объема товарооборота составило 9,7%
4) Общий индекс товарооборота в фактический ценах найдем по формуле:
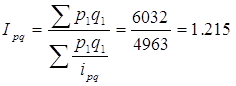
или 121,5%. Выручка от продаж всех товаров в среднем выросла на 21,5%.
5) Абсолютный прирост товарооборота вследствие изменения:
а) цен
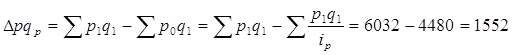 (см.гр.8)
(см.гр.8)
б) объема продажи:
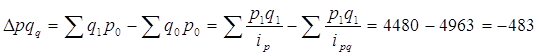 (см. гр.9)
(см. гр.9)
в) двух факторов вместе
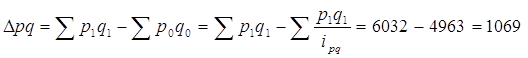 (см.гр. 10)
(см.гр. 10)
Вычисления абсолютного прироста товарооборота вследствие изменения объема продажи по каждому району см. гр. 8-10 табл.2.
Проверка взаимосвязи индексов
![]()
![]()
Задача №2
Динамика объема продукции и затрат на ее производство характеризуется данными:
| Вид продукции | Фактические затраты на производство, тыс. руб. | Индекс физического объема продукции 2 кв. к 1 кв., % | |
| 1 квартал | 2 квартал | ||
| А | 300 | 360 | 105 |
| Б | 200 | 250 | 90 |
Определите общие индексы:
1. физического объема продукции;
2. себестоимости продукции;
3. абсолютный прирост (снижение) затрат за счет изменения: объема продукции, себестоимости продукции.
Решение:
Таблица 4
| Вид продукции | Фактические затраты на производство |
|
| |
|
|
| |||
| А | 300 | 360 | 1,05 | 315 |
| Б | 200 | 250 | 0,90 | 180 |
| 500 | 610 | 495 | ||
1) Найдем индекс физического объема по следующей формуле:
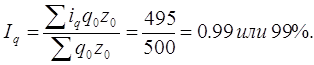
Среднее снижение физического объема продукции составило 1%.
2) Вычислим индекс себестоимости продукции:
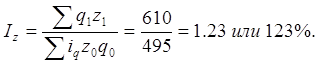
Среднее увеличение себестоимости на произведенную продукцию составило 23%.
3) Абсолютное изменение затрат за счет изменения:
а) объема продукции
![]()
б) себестоимости продукции
![]()
![]()
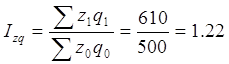
в) 2-х факторов вместе
![]()
![]()
Проверка взаимосвязи:
![]()
III. Аналитическая часть
Согласно Российскому статистическому ежегоднику 2004 года имеются следующие данные:
Таблица 5
| Регионы | Товарооборот, млн. руб. | Индексы физического объема товарооборота в отчетном году по сравнению с базисным (в сопоставимых ценах, %) | |
| 2002 г. | 2003 г. | ||
| Воронежская обл. | 43512 | 52609 | 109,0 |
| Курская обл. | 18700 | 23240 | 111,0 |
| Московская обл. | 153803 | 194375 | 115,6 |
[см. стр. 497, 501]
Следует определить:
1) среднее изменение цен на товары по каждому региону.
2) общий индекс цен по трем регионам.
3) общий индекс физического объема товарооборота.
4) общий индекс товарооборота в фактических ценах.
5) абсолютный прирост товарооборота вследствие изменения цен, объема продажи по каждому региону и в целом по трем регионам.
Решение:
Таблица 6
| Регионы |
|
|
|
|
|
|
|
|
|
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 1 | 43512 | 52609 | 1,09 | 1,209 | 1,109 | 47438 | 43514 | 5171 | 3924 | 9095 |
| 2 | 18700 | 23240 | 1,12 | 1,243 | 1,12 | 20750 | 18697 | 2490 | 2053 | 4543 |
| 3 | 153803 | 194375 | 1,156 | 1,264 | 1,093 | 177836 | 153778 | 16539 | 24058 | 40597 |
| 270224 | 246024 | 215989 | 24200 | 30035 | 54235 |
Расчеты данных таблицы 6 с помощью MS Excel:
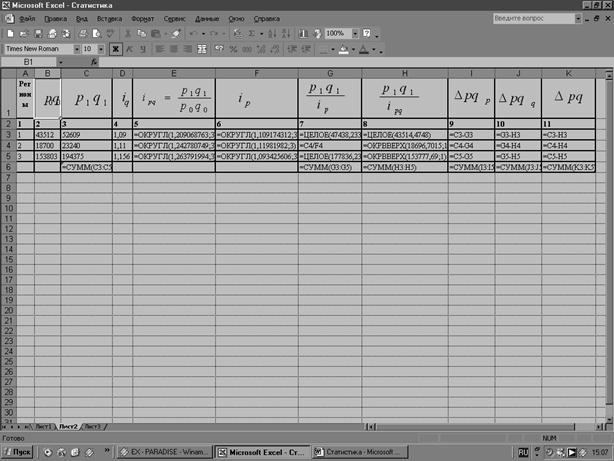
Таблица 7
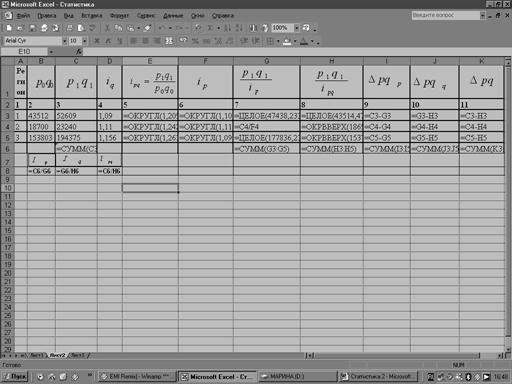
Таблица 8
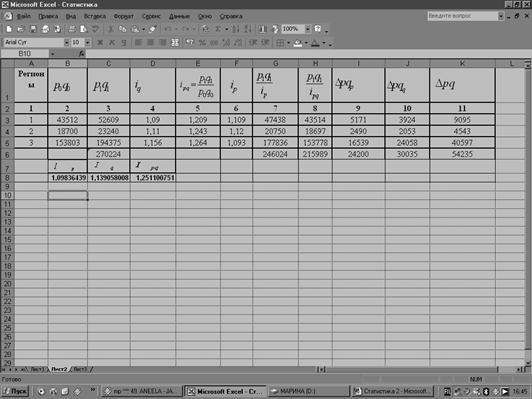
Таблица 9
1) Для того, чтобы узнать среднее изменение цен на товары по каждому региону произведем вычисления по следующей формуле:
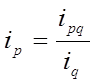 (см. гр.6 табл.5)
(см. гр.6 табл.5)
а) 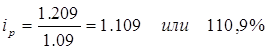 ; Среднее повышение цен на товары в Воронежской области составило 10,9%.
; Среднее повышение цен на товары в Воронежской области составило 10,9%.
б) 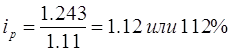 ; Среднее повышение цен на товары в Курской области составило 12%.
; Среднее повышение цен на товары в Курской области составило 12%.
в) 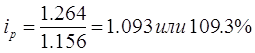 ; Среднее повышение цен на товары в Московской области составило 9,3%.
; Среднее повышение цен на товары в Московской области составило 9,3%.
2) Определим общий индекс цен по трем регионам по формуле среднего взвешенного гармонического индекса.
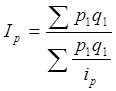 .
.
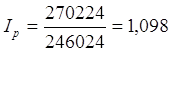
или 109,8%. Среднее повышение цен в общем по трем регионам составило 9,8%.
3) Найдем общий индекс физического объема товарооборота.
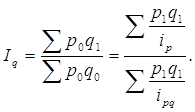
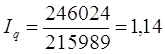
или 114%. Среднее повышение физического объема товарооборота составило 14%
4) Общий индекс товарооборота в фактический ценах найдем по формуле:
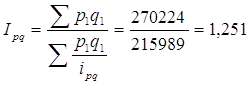
или 125,1%. Выручка от продаж всех товаров в среднем выросла на 25,1%.
5) Абсолютный прирост товарооборота вследствие изменения:
а) цен
![]() (см.гр.9)
(см.гр.9)
б) объема продажи:
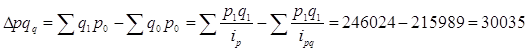 (см. гр.10)
(см. гр.10)
в) двух факторов вместе
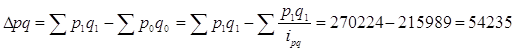 (см.гр. 11)
(см.гр. 11)
Вычисления абсолютного прироста товарооборота вследствие изменения объема продажи по каждому региону см. гр. 9-11 табл.5.
Проверка взаимосвязи индексов
![]()
![]()
Заключение
Индексы относятся к важнейшим обобщающим показателям. С помощью экономических индексов можно измерить динамику социально-экономического явления за два и более периодов времени, динамику среднего экономического показателя и сопоставить уровни явления в пространстве: по странам, экономическим районам, областям и т.д. Индексы широко используются также для определения степени влияния измерений значений одних показателей из фактических цен в сопоставимые.
В практике статистики индексы наряду со средними величинами являются наиболее распространенными статистическими показателями. С их помощью характеризуется развитие национальной экономики в целом и ее отдельных отраслей, анализируются результаты производственно-хозяйственной деятельности предприятий и организации, исследуется роль отдельных факторов в формировании важнейших экономических показателей, выявляются резервы производства, индексы используются также в международных сопоставлениях экономических показателей, определения уровня жизни, мониторинге деловой активности в экономике и т.д.
Обычно сопоставляемые показатели характеризуют явления, состоящие из разнородных элементов, непосредственное суммирование которых невозможно в силу их несоизмеримости. Например, промышленные предприятия выпускают, как правило, разнообразные виды продукции. Получить общий объем продукции предприятия в таком случае нельзя суммированием количества различных видов продукции в натуральном выражении. Здесь возникает проблема соизмерения разнородных элементов. В качестве меры соизмерения разнородных продуктов можно использовать цену, себестоимость или трудоемкость единицы продукции.
С помощью индексных показателей решаются следующие основные задачи:
1) характеристика общего изменения сложного экономического показателя (например, затрат на производство продукции, стоимости произведенной продукции и т.д.) или формирующих его отдельных показателей-факторов;
2) выделение в изменении сложного показателя влияния одного из факторов путем элиминирования влияния других факторов (например, увеличение выручки от реализации продукции, связанное с ростом цен или выпуска продукции в натуральном выражении). В качестве самостоятельной выделяется задача обособления влияния изменения структуры явления на индексируемую величину. Например, при изучении динамики среднеотраслевой себестоимости продукции исследуется влияние измерения в распределении объемов выпуска продукции по предприятиям отрасли.
Способы построения индексов зависят от содержания изучаемых показателей, методологии расчета исходных статистических показателей, имеющихся в распоряжении исследователя статистических данных и целей исследования.
Индексные показатели в статистике вычисляются на высшей ступени статистического обобщения и опираются на результаты сводки и обработки данных статистического наблюдения.
Список используемой литературы
1. Гусаров В.М. Статистика: Учеб. Пособие для вузов – М.: ЮНИТИ-ДАНА, 2001.- 463с.
2. Статистика: Курс лекций (Харченко Л. П., Долженкова В.Г., Ионин В.Г. и др.; Под ред. к.э.н. В.Г. Ионина. – Новосибирск: Изд-во НГАЭиУ, М.: ИНФРА-М, 1999. – 310 с.
3. Статистика: Учеб. Пособие/А.В. Багот, М.М. Конкина, В.М. Симчеры и др. – М.: Финансы и статистика, 2005.- 368 с.
4. Общая теория статистики: Статистическая методология в изучении коммерческой деятельности: Учеб./ Под ред. О.Э. Башиной, А.А. Спирина. – 5-е изд., доп. И перераб. – М.: Финансы и статистика, 2005. – 440с.
5. Ряузов Н.Н. Общая теория статистики: Учеб. Для студ. Эконом. Спец. Вузов – 3-е изд., перераб. И доп. – М.: Статистика, 1980 – 344с.
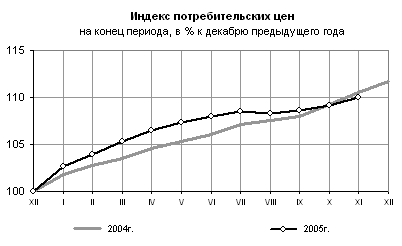
[1] Индекс потребительских цен (ИПЦ), см. Гусаров В.М. глава 21.3.
Похожие работы
... реальных ценах сделок, осуществлённых самой компанией. В данном случае выборка является очень похожей и пока не может быть иначе. Российский рынок ценных бумаг не имеет пока ещё золотой прослойки и делится на явных лидеров (порядка 20 компаний) и аутсайдеров. Е) Индексы ДЭК. Довольно интересными и перспективными специалисты считают индексы еженедельника «Деловой экспресс» (индекс ДЭК-1 и серия ...
... в индексном отношении определённые экономические категории. Пример. Таблица 1. Товар Ед. базисный отчетный Индивидуальные изм. период период индексы цена за единицу кол-во цена за единицу кол-во, цен Физическ. объёма товара, руб. товара, руб. ...
... . Динамические индексы бывают базисными и цепными. Вторая группа индексов (территориальные) применяется для межрегиональных сравнений. Большое значение эти индексы имеют в международной статистике при сопоставлении показателей социально-экономического развития различных стран. Например, индекс цен на автомобили в США по сравнению с Японией, индекс стоимости потребительской корзины в Москве по ...
... применение данных методов значительно улучшает анализ внешней торговли, вскрывает неиспользованные резервы, тем самым способствуя в целом повышению эффективности ВЭС. 3.МЕТОДОЛОГИЯ ПРИМЕНЕНИЯ ИНДЕКСНОГО МЕТОДА В ТАМОЖЕННОЙ СТАТИСТИКЕ В качестве первичной исходной информации при формировании индексов внешней торговли РФ используются данные, содержащиеся в грузовых таможенных декларациях (ГТД ...
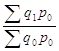
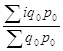
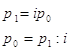
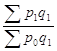
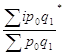
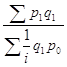
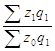

0 комментариев