Статистика

Основные характеристики и графическое изображение

вариационного ряда.

Понятие вариационного ряда.

Первичные статистические данные часто представлены неупорядоченной последовательностью чисел, характеризующих ту или иную сторону процесса. В этой совокупности чисел бывает трудно разобраться и первичная обработка материалов сводится к приведению имеющихся данных к виду, удобному для анализа.

Пример: При исследовании студентов первого курса по возрасту были зафиксированы следующие данные:

17 18 18 18 19 18 20 20 19 18 18 21 19 22 23 18 19 19 19 21 21 18 18 18 18 22 19 18 20 18 19 18 20 19 21 20 22 18 19 21 19 19 22 23 19 20 21 22 17 19

Полученный в результате обследования ряд чисел в дальнейшем будем называть статистической совокупностью, а сами числа показывающие изменения (вариацию) подлежащего изучению признака – вариантами (обозначим их X_i, где I - номер варианта).

Если упорядочить совокупность исходных данных в убывающем или возрастающем порядку то получим так называемый ранжированный ряд.

Используем для упорядоченной таким образом совокупности более компактную запись, представляем ее в виде таблицы. В первой колонке поставим различающиеся по величине варианты, расположив их в возрастающем порядке, во второй – числа, показывающие, как часто, встречаются отдельные значения вариант (назовем их частотами и обозначим N_i).

Распределение студентов первого курса по возраст

табл. 1

Возраст студентов (варианты Xi)	Число студентов с данным возрастом (частоты Ni)
17 18 19 20 21 22 23	2 15 14 6 6 5 2
ИТОГО	50

Полученный ряд называется вариационным. Сведение первичных данных в вариационный ряд облегчит анализ совокупности так, например, видно, что в обследованной группе чаще встречаются студенты в возрасте 18-19 лет, меньше всего студентов 17 лет и 23.

Основные характеристики вариационного ряда.

Построение вариационного ряда является только первым шагом в изучении статистических данных. Для более глубокого исследования материала необходимы обобщающие количественные показатели, вскрывающие общие свойства статистической совокупности. Эти показатели, во-первых, дают общую картину, показывают тенденцию развития процесса или явления, нивелируя случайные индивидуальные отклонения, во-вторых, позволяют сравнивать вариационные ряды и, наконец, используются во всех разделах статистики при более полном и сложном анализе статистической совокупности.

Существуют две группы характеристик вариационного ряда:

1.         меры уровня, или средние;

2.         меры рассеяния.

Меры уровня, или средние.

Наиболее употребительными в статистических исследованиях являются три вида средних: средняя арифметическая, мода и медиана.

Выбор типа средней для характеристики вариационного ряда зависит от цели, для которой исчисляется средняя, от особенностей исходного материала и от возможностей той или иной средней.

Прежде чем перейти к характеристике отдельных видов средней, сформулируем некоторые, самые общие требования к средней.

Средняя, представляет собой количественную характеристику качественно однородной совокупности. Нарушение этого требования приводит к неверным выводам, искажает суть явления.

Кроме того, необходимо, чтобы средняя не была слишком абстрактной, а имела ясный смысл в решении задачи.

Далее, желательно, чтобы процедура вычисления средней была проста. При прочих равных условиях предпочтение отдается той средней, которая проще вычисляется.

При выборе средней желательно свести к минимуму влияние случайных колебаний выборки. Так, если одной и той же совокупности взять несколько групп элементов, то средние, им соответствующие, будут, как правило, различаться по величине. Рекомендуется использовать вид средней, у которой эти различия минимальны.

Наиболее распространенной мерой уровня – является средняя арифметическая.

 

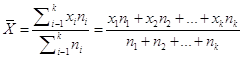
где - знак суммирования от 1 до k; X_i– варианты с порядковым номером i;  = n – объем совокупности (число элементов совокупности); n_i – частота варианта x_i; k – число варианта. Если вместо частоты заданы частости q_i, то формула имеет вид

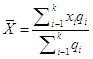
где  = 1, или 100%.

Пример:

Вычислим средние размеры наделов крестьян по данным табл. 1.

Для решения задачи, прежде всего, необходимо найти середины интервалов. Определенная трудность возникает в связи с тем, что первый и последний интервалы являются открытыми. Нижнюю границу первого интервала естественно принять равной нулю. Тогда середина этого интервала равна (0+2)/2=l. Для нахождения центрального значения последнего интервала применим предложенный выше прием. Величина интервала, предшествующего последнему, равна 2. Условно принимаем за величину последнего интервала 2. Тогда верхняя граница того интервала-9 и, следовательно, его середина вычисляется так: (7+9)/2=8.

Пользуясь формулой средней арифметической и принимая за значение признака середину интервала (строка 2 табл.2), рассчитываем средний дореформенный надел у барщинных крестьян:

Аналогично вычисляется средний дореформенный надел у оброчных крестьян: .

Табл.2

Размеры дореформенного надела у крестьян

	надел xi, дес
	до 2	С 2 до 3	С 3 до 5	С 5 до 7	Свыше 7
середина интервалов проценет барщинных крестьян qt(1) процент оброчных крестьян qt(2)	1.0 1.8 12.4	2.5 18.4 17.5	4.0 63.5 48.2	6.0 15.2 13.3	8.0 1.1 8.6

Кроме средней арифметической широкое распространение имеет другой вид мер уровня - медиана.

Медианой (обозначим M_е) называется такое значение варьирующего признака, которое приходится на середину вариационного ряда.

При нахождении медианы дискретного вариационного ряда могут возникнуть два случая: 1) число вариант нечетно (k=2m+1), 2) число вариант четно (k=2m). В первом случае M_e=x_m+1, т. е. медиана равна центральной (срединной) варианте ряда, во втором случае M_e,=(x_m+x_m+1)/2, т.е. медиана принимается равной полу сумме находящихся в середине ряда вариант.

Пусть дан ряд с нечетным числом вариант:

X1	X2	X3	X4	X5	X6	X7	X8	X9
8	9	11	12	15	16	18	19	19

Тогда число вариант, равное 9, представимо в виде 2m+1=9, откуда 2m=8, m=4, т.е.M_e=x₄₊₁=x₅=15.

Рассмотрим случай четного числа членов:

X1	X2	X3	X4	X5	X6	X7	X8	X9	X10	X11	X12
8	9	11	12	15	16	18	19	19	23	24	40

Здесь 2m = 12, m = 6 и

Для интервального вариационного ряда медиана вычисляется по формуле

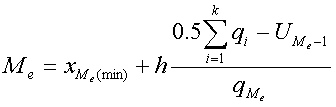
где x_Me(min)-нижняя граница медианного интервала; h - величина этого интервала, или интервальная разность; q_i- частоты или частости; - накопленная сверху частота (или частость) интервала, предшествующего медианному; частота или частость медианного интервала.

Пример: Вычислим медиану по данным табл. 3.

Распределение хозяйств русских переселенцев Чимкентского уезда по размеру посева (1902г.)

Размер посева xi дес.	Всего хозяйства qi %	Накопленные частости Ui	Плотность распределения fi
0-4 4-8 8-12 12-20 20-30 Более 30	16,6 24,4 19,1 23,9 9,7 6,3	16,6 41,0 60,1 84,0 93,7 100,0	4,15 6,10 4,78 2,99 0,97

Вычисление медианы начинается с нахождения интервала, содержащего медиану. Медианному интервалу соответствует первая из накопленных частот или частостей, превышающая половину всего объема совокупности. В нашем случае объем совокупности равен 100%, первая из накопленных частостей, превышающая половину всего объема совокупности, - 60,1 (см. табл. 6). Следовательно, интервал 8-12 будет медианным. Далее, x_me(min)=8, h=4, =41, q_Me=19.1. Воспользуемся формулой:

Таким образом, серединный размер посева равен примерно 9,9 дес.

Медиану можно использовать в тех случаях, когда изучаемая совокупность неоднородна, и в такой ситуации она будет иметь вполне конкретный смысл. Так, в рассмотренном примере значение медианы имеет следующий смысл: у одной половины хозяйств размер посева меньше, у другой половины - больше, чем 9,9 дес.

Особо важное значение медиана приобретает при анализе асимметричных рядов, т. е. рядов, у которых нагружены (имеют большие частоты) крайние или близкие к крайним значения вариант. Например, медиана даст более верное представление о среднем уровне личных доходов группы семей в капиталистических странах, чем средняя арифметическая, так как медиана не столь чувствительна к край ним (нетипичным в плане постановки задачи) значениям (семьи с большим доходом), как средняя арифметическая.

Медиану следует применять, если вычисление средней арифметической неправомерно вследствие неопределенности интервалов (первого или последнего, или того и другого вместе).

К достоинствам медианы следует отнести также то, что она менее подвержена случайностям выборки, чем средняя арифметическая.

Медиану не следует использовать, когда число наблюдений невелико.

Наряду со средней арифметической и медианой важное значение как мера уровня имеет мода.

Модой (обозначим М_о) называется варианта, наиболее часто встречающаяся в данном вариационном ряду.

Для дискретного ряда мода равна варианте с наибольшей частотой или частостью.

Для интервального вариационного ряда модальный интервал, т. е. интервал, содержащий моду, определяется по наибольшей' частоте (частости) в случае равных интервалов и по наибольшей плотности в случае неравных интервалов. Значение варианты, равное моде, отыскивается приближенными методами.

Довольно грубое приближение можно получить, взяв за моду центральное значение модального интервала, т. е. среднее арифметическое границ интервала.

Пример:

Вычислим моду по данным табл. 3. В последнем столбце табл. 3 вычислены плотности распределения.

Наибольшая плотность соответствует интервалу 4-8. Это и есть модальный интервал.

Рассчитываем моду: M_o=(4+8)/2=6 (дес.).

Таким образом, получаем, что наиболее типичным по размеру посева хозяйством русских переселенцев, Чимкентского уезда в 1908 г. было хозяйство, засевавшее 6 дес. земли.

Моду можно вычислить также как взвешенную среднюю арифметическую из нижней и верхней границ модального интервала (весами в расчете будут служить частоты или частости интервалов предмодального и послемодального). При этом если ряд построен правильно и интервалы, соседние с модальными, мало отличаются друг от друга, т. е. распределение близко к симметричному, то этот способ дает хорошие результаты.

Воспользовавшись вторым методом исчисления моды, рассчитаем наиболее типичный размер посева по данным табл. 3:

(дес.)

Мода имеет те же достоинства, что и медиана. Мода и медиана эффективно используются в качестве мер уровня, но сравнительно со средней арифметической реже употребляются как исходный материал для более сложных методов статистики.

Меры рассеяния. Рассмотренные выше средние показывают уровень вариационного ряда, другими словами, позволяют ряд чисел охарактеризовать одним числом. Однако средние не содержат в себе информации о том, насколько хорошо они представляют всю совокупность. Одинаковые или близкие по величине средние могут относиться к весьма различным рядам. Для пояснения этого положения рассмотрим условный пример.

Пример: В табл. 4 приведены данные о возрасте.

	1	2	3	4	5	Всего
1 группа 2 группа	31 14	32 15	36 15	40 66	41 70	180 180

Рассчитав, получаем, что средний возраст в 1-ой и 2-ой группах одинаков и равен 36. Но простейшее сравнение этих двух рядов показывает, что одинаковые средние представляют две совершенно различные по возрастному составу группы, а именно: в 1-ю группу входят люди в зрелом возрасте, тогда как во 2-ю-старики и дети. Иначе говоря, варианты первого ряда довольно тесно группируются вокруг своей средней, т. е. средняя представительна, тогда как во втором ряду обнаруживается сильный разброс (рассеяние) вариант. Чтобы отметить подобные различия, в статистике прибегают к расчету показателей, характеризующих рассеяние признака (мер рассеяния).

Рассмотрим основные меры рассеяния: размах вариации, дисперсию и среднее квадратичное отклонение.

Размах вариации показывает разность между наибольшим и наименьшим значениями признака (R=x_max-x_min). Достоинством этого показателя является простота расчета. Однако возможности его применения ограничены, так как эта характеристика является наиболее грубой из всех мер рассеяния.

Во-первых, при расчете этого показателя рассеяния признака используются только крайние значения признака, остальные же во внимание не принимаются. Во-вторых, размах вариации существенно зависит от случайных колебаний выборка.

Более ценными для характеристики рассеяния признака являются показатели, при расчете которых используются отклонения всех вариант от некоторой средней (например, средней арифметической, медианы). К таким мерам рассеяния, в частности, относятся дисперсия и среднее квадратичное отклонение. Последние меры рассеяния меньше любой другой меры подвержены случайным колебаниям выборки. Среднее квадратичное отклонение и дисперсия нашли широкое применение почти во всех разделах статистики.

Дисперсия, или средний квадрат отклонения (обозначим σ²) есть средняя арифметическая из квадратов отклонений вариант от их средней арифметической, т. е. в математической записи

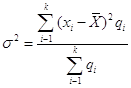
где x_i-варианта с порядковым номером i; - средняя арифметическая; k- число вариант; q_i-частота или частость с порядковым номером I.

Часто для исследования удобно представлять меру рассеяния в тех же единицах измерения, что и варианты. Тогда вместо дисперсии используют среднее квадратичное отклонение, которое является квадратным корнем из дисперсии, т. е. среднее квадратичное отклонение вычисляется по формуле

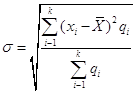
Пример: Рассмотрим распределение дореформенного надела у крестьян Симбирской губернии отдельно для группы барщинных и группы оброчных крестьян (табл.2). Средние величины дореформенных наделов для обеих групп крестьян оказались практически равными (4,018 дес. у барщинных и 3,976 у оброчных). Выясним, насколько одинаковой была вариация показателей в этих группах. С этой целью вычислим средние квадратичные отклонения по совокупности барщинных и по совокупности оброчных крестьян.

Табл. 5 Данные для вычисления среднеквадратичного отклонения.

Размер наделов, дес.	Середина интервалов xi	Барщинные крестьяне				Оброчные крестьяне
		qi				qi
До 2 2-3 3-5 5-7 Свыше 7	1,0 2,5 4,0 6,0 8,0	1,8 18,4 63,5 15,2 1,1	3,0 1,5 0 2,0 4,0	9,0 2,2 0 4,0 16,0	16,2 40,5 0 60,8 17,6	12,4 17,5 48,2 13,3 8,6	111,6 38,5 0 53,2 137,6
Итого		100,0			135,1		340,9

Для вычисления средних квадратичных отклонений удобно составить вспомогательную таблицу (табл. 5). В ней зафиксированы все промежуточные расчеты. Подставляя результаты этих расчетов в формулу

,

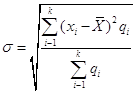получим среднее квадратичное отклонение для барщинных крестьян:

и среднее квадратичное отклонение для оброчных крестьян:

т е. колебание признака у оброчных крестьян примерно в полтора раза больше, чем у барщинных.

Таким образом, средняя величина дореформенного надела у барщинных и оброчных крестьян Симбирской губернии почти одинакова, т. е. в среднем эти группы крестьян по обеспеченности землей практически не отличаются. Но в среде оброчных крестьян различия в размере наделов больше, чем среди барщинных крестьян.

Рассмотренные выше меры рассеяния (размах вариации, дисперсия, среднее квадратичное отклонение) являются абсолютными величинами, судить по ним о степени колеблимости признака не всегда можно, в некоторых задачах необходимо использовать относительные показатели рассеяния. Таким показателем является коэффициент вариации.

Коэффициент вариации (обозначим V) представляет собой отношение среднего квадратичного отклонения к средней арифметической, выраженное в процентах, т. е.

Коэффициент вариации позволяет: 1) сравнивать вариацию одного и того же признака у разных групп объектов, 2) выявить степень различия одного и того же признака у одной и той же группы объектов в разное время, 3) сопоставить вариацию разных признаков у одних и тех же групп объектов.

Графическое представление вариационных рядов.

Существуют несколько способов графического изображения рядов (гистограмма, полигон, кумулята), выбор которых зависит от цели исследования и от вида вариационного ряда.

Полигон распределения в основном используется для изображения дискретного ряда, но можно построить полигон и для интервального ряда, если предварительно привести его к дискретному. Полигон распределения представляет собой замкнутую ломаную линию в прямоугольной системе координат с координатами (x_i, q_i), где x_i – значение i-го признака, q_i – частота или частость i-го признака.

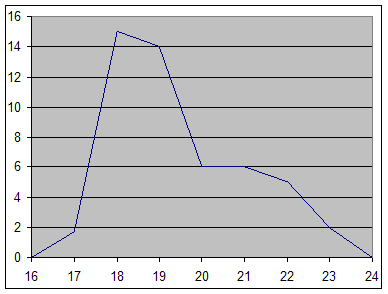
Пример: Построим полигон распределения по данным табл. 1. В прямоугольной системе координат на горизонтальной оси откладываем значения признака (возраст студентов), а на вертикальной оси - частоты (число студентов с данным возрастом). Полученные точки соединим отрезками прямой. Для того чтобы фигура была замкнутой, введем дополнительно новые значения признака (16 лет, 24 года); соответствующие им частоты, естественно, равны нулю. В результате получим полигон распределения студентов по возрасту (рис. 1).

Рис.1 Полигон распределения студентов по возрасту.

 

Гистограмма распределения применяется для изображения интервального ряда. Для построения гистограммы на горизонтальной оси откладывают последовательно отрезки, равные интервалам признака, и на этих отрезках, как на основаниях, строят прямоугольники, высоты которых равны частотам или частностям для ряда с равными интервалами, плотностям; для ряда с неравными интервалами.

Пример: Построим гистограмму распределения душ по размеру прирезки в Бельском уезде Смоленской губернии по данным табл. 6 (рис 2) (За неимением дополнительных данных при построении графика воспользуемся предположением, что величина последнего открытого интервала равна величине предыдущего).

Табл.6

Размер прирезки xi, %	Количество душ, к наделам которым сделаны прирезки qi, %
До 10 11-20 21-30 31-40 41-50 Свыше 50	24,5 26,7 19,3 9,7 5,8 14,0

Рис.2 Гистограмма распределения душ по размеру прирезки.

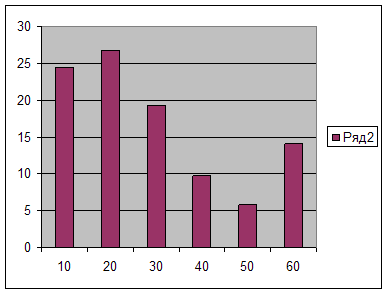
Как уже отмечалось, для интервального ряда также можно построить полигон распределения. Для этого за значение признака принимают середины интервалов и для получения дискретного ряда обычным способом строят полигон. Полигон распределения можно получить и по готовой гистограмме. Достаточно соединить отрезками прямых середины верхних оснований прямоугольников и замкнуть фигуру. Результаты такого построения изображены пунктирной линией на рисунке 2.

Кумулята есть графическое изображение вариационного ряда, когда на вертикальной оси откладываются накопленные частоты или частности, а на горизонтальной - значения признака. Кумулята служит для графического представления как дискретных, так и интервальных вариационных рядов.

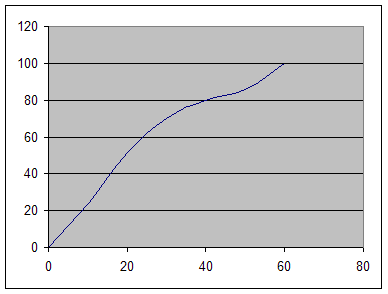
Пример: Построим кумуляту по данным интервального ряда таблицы 6. Предварительно рассчитав накопленные частости.

Размер прирезки	частости	Накопленные частости
До 10 11-20 21-30 31-40 41-50 51-60	24,5 26,7 19,3 9,7 5,8 14,0	24,5 51,2 70,5 80,2 86,0 100,0

Рис. 3 Кумулята

Показатели статистики бедности. Понятие прожиточного

минимума, потребительской корзины.

 

Показатели, характеризующие неравенство, используются для решения широкого круга взаимосвязанных экономических и социальных вопросов. Среди многообразия видов неравенства в большей степени поддающимся статистическому измерению считается экономическое неравенство. Оно представляет собой различия между отдельными группами населения по величине получаемых ими доходов. В конечном счете именно неравенство в доходах определяет неравенство в уровне расходов и потребления и приводит к одной из самых критических форм его проявления – бедности.

Статистическое измерение неравенства предназначено, главным образом, для 1) определения пропорций, в которых основные виды доходов распределяются среди населения; 2) выявления факторов, влияющих на наблюдаемые пропорции; 3) определение уровня благосостояния различных групп населения и выявление групп, находящихся в неблагоприятном положении, зажиточных, богатых и т.п.; 4) выявление некоторых характеристик и аспектов условий жизни стратифицированных групп населения, которые являются причиной различия в их положении.

Статистическое измерение неравенства доходов базируется на принципе сравнения уровня доходов между однородными категориями домашних хозяйств и населения, сгруппированными по показателям, которые или представляют непосредственно уровень дохода или находится в тесной взаимосвязи с ним. Сравнение доходов возможно проводить на индивидуальном уровне или на уровне домохозяйства в целом. Как правило, наиболее предпочтительной единицей для измерения неравенства выступает домохозяйство, а степень неравенства определяется как разница показателей доходов на члена домохозяйства (или домохозяйство в целом).

Агрегирование индивидуальных доходов на уровне домохозяйства позволяет включить в оценку неравенства все источники доходов населения. В отличии от этого, сравнение доходов на уровне индивидуальной заработной платы не дает такого представления, поскольку в этом случае из поля зрения выпадают выплаты населению по линии социального обеспечения, а также другие доходы, которые возможно учесть только в контексте семьи (например, доходы от собственности, принадлежащей всем членам домохозяйства). Важно отметить, что при определении показателей доходов на одного члена домохозяйства предполагается, что весь объем дохода распределяется между членами домохозяйства (как получателями дохода, так и иждивенцами) в равной пропорции. Таким образом, степень неравенства на основе доходов домохозяйства игнорируют неравенство между доходами каждого из получателей, а следовательно, и каждого источника доходов, что приводит к некоторому смещению по сравнению с оценками неравенства на основе индивидуальной заработной платы.

Для проведения сравнительного анализа доходов различных групп домашних хозяйств и населения используются следующие виды классификаций.

Классификации по характеристикам домашних хозяйств. Среди них выделяются, главным образом, классификация по размеру домашних хозяйств и классификация по числу зарабатывающих лиц в домашних хозяйствах. Каждая из них должна не только показывать общее число лиц(как в домашнем хозяйстве, так и в составе категории зарабатывающих), но также выделять их важные возростно половые характеристики(несовершеннолетние, в трудоспособных и старших возрастных категориях). Кроме того, важное значение для понимания различий в уровнях доходов также имеют вид деятельности, профессия и уровень образования глав домашних хозяйств.

Классификация по характеристикам лиц. Эти классификации относятся к их месту проживания, возрасту, полу, социально-экономическому положению и уровню образования. Классификации населения по социально-экономическому положению, как правило, строятся на различных сочетаниях систем классификации, таких как основной источник средств к существованию, положение в занятии, принадлежность к виду экономической деятельности и профессии. В группах экономически активных проводится различия между работниками наемного труда и предпринимателями. Экономически не активные лица, проживающие в домашних хозяйствах, подразделяются на лиц, живущих в основном на пенсии, пособия по социальному страхованию, стипендии и аналогичные трансферты от государственных и некоммерческих учреждений. Среди них также выделяются лица, живущие в основном на доходы от собственности.

Наиболее важной классификацией различных групп населения и домашних хозяйств, позволяющем в конечном итоге провести статистическое измерение неравенства, является группировка населения (или домохозяйств) по уровню доходов, выраженная либо интервальным рядом распределения (в абсолютном выражении), либо распределением общественного объема доходов по квантильным группам.

Методы измерения бедности.

В экономической и статистической литературе используются различные подходы для измерения бедности. Различают следующие методы измерения бедности населения:

1. абсолютный, исходя из совокупности стоимости оценки прожиточного минимума, который определяется нормативным методом с помощью научно обоснованных нормативов потребления;

2. относительный, исходя из сложившихся соотношений в распределении доходов по различным группам населения;

3. субъективный, основанный на обследовании общественного мнения об уровне низких или не достаточных доходов (опирается на мнениях опрашиваемых по типу: «Я считаю, что такой – то доход для семьи, состоящей из стольких-то человек, низкий, достаточный, хороший, очень хороший»).

Абсолютный подход – абсолютная бедность. Это понятие является основой наиболее «официальных» определений низкого дохода. Бедными считают тех, кто в несостоянии обеспечить себя суммой благ для удовлетворения основных потребностей в пище, одежде, жилище, для сохранения здоровья и ведения умеренно активной трудовой жизни. Абсолютно бедным считается тот человек, доходы которого находятся ниже некоторого установленного минимума. При использовании критерия абсолютной бедности уровень бедности и численность бедных зависит от границы бедности, официально установленной государством, которая, в свою очередь, зависит от финансовых возможностей государства.

Таким образом, при изучении абсолютной бедности необходимо решить две основные задачи: