Навигация
Корреляционный анализ использования оборотных средств
5. Корреляционный анализ использования оборотных средств
В статистике оборотных фондов находит применение корреляционно–регрессионный анализ. С помощью данного метода решаются две задачи статистико-экономического анализа:
§ Определения наличия связи между явлениями с помощью математического уравнения;
§ Определение степени тесноты связи с помощью коэффициентов корреляции и детерминации.
Линейная регрессия одного фактора
Уравнение линейной регрессии одного фактора записывается в виде уравнения прямой: ![]()
![]() +
+![]() , где
, где ![]() - факторный признак;
- факторный признак; ![]() - результативный признак;
- результативный признак; ![]() и
и ![]() - параметры уравнения. Чтобы определить параметры пользуются методом наименьших квадратов и находят минимум функций S= Σ (
- параметры уравнения. Чтобы определить параметры пользуются методом наименьших квадратов и находят минимум функций S= Σ (![]() -
- ![]() -
-![]() )
)![]() . В этой функции за переменные принимаются последовательно значения
. В этой функции за переменные принимаются последовательно значения ![]() и
и ![]() . Экстремум функции двух переменных определяется, если приравнять частные производные по этим переменным нулю.
. Экстремум функции двух переменных определяется, если приравнять частные производные по этим переменным нулю.
После определения частных производных функции по ![]() и
и ![]() , приравнивания их нулю, и небольших преобразований получим систему нормальных уравнений:
, приравнивания их нулю, и небольших преобразований получим систему нормальных уравнений:
![]()
![]()
![]() +
+![]() Σ
Σ![]() = Σ
= Σ![]() ;
;
![]() Σ
Σ![]() +
+![]() Σ
Σ![]() = Σ
= Σ![]() ,
,
Решение которой и позволяет определить величины параметров ![]() и
и ![]() , а следовательно и уравнение регрессии.
, а следовательно и уравнение регрессии.
Параметры уравнения линейной регрессии одного фактора можно находить и по формулам:
![]() =
=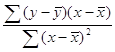 ;
; ![]() =
=![]() -
- ![]() .
.
Ясно, что практически приемлемым является наименее трудоемкий вариант расчета. В уравнении прямой параметр ![]() экономического смысла не имеет. Параметр
экономического смысла не имеет. Параметр ![]() является коэффициентом регрессии и показывает изменение результативного признака при изменении факторного признака на единицу.
является коэффициентом регрессии и показывает изменение результативного признака при изменении факторного признака на единицу.
Кроме линейной функции связи в экономическом анализе часто применяются степенная, гиперболическая и параболическая функции.
Расчет параметров степенной функции
Если значения факторного признака расположены в порядке геометрической прогрессии и соответствующие значения результативного признака также образуют геометрическую прогрессию, то связь между признаками может быть представлена степенной функцией вида
![]()
Для определения параметров степенной функции методом наименьших квадратов необходимо привести ее к линейному виду путем логарифмирования:
![]() .
.
Система нормальных уравнений имеет вид:
![]()
![]() Σ
Σ![]() Σ
Σ![]() ,
,
![]() Σ
Σ![]() Σ
Σ![]() Σ
Σ![]() .
.
Параметры можно определить, решая систему нормальных уравнений или по формулам:
 ,
, 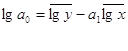 .
.
Расчет параметров уравнения гиперболы
Если результативный признак с увеличением факторного признака возрастает (или убывает) не бесконечно, а стремится к конечному пределу, то для анализа такого признака применяется уравнение гиперболы вида
![]() .
.
Для определения параметров этого уравнения используется система нормальных уравнений
![]() Σ
Σ![]() Σ
Σ![]() ,
,
Σ![]() Σ
Σ![]() Σ(
Σ(![]() )
)![]() .
.
Чтобы определить параметры уравнения гиперболы методом наименьших квадратов, необходимо привести его к линейному виду. Для этого произведем замену переменных ![]() =
=![]() , получим следующую систему нормальных уравнений:
, получим следующую систему нормальных уравнений:
![]() Σ
Σ![]() Σ
Σ![]() ,
,
Σ![]() Σ
Σ![]() Σ
Σ![]() .
.
Параметры уравнения гиперболы можно вычислить по формулам
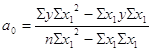 ,
,
![]() .
.
Параболическая регрессия одного фактора
Связь одного фактора, при которой результативный признак увеличивается быстрее, чем факторный, отображается уравнением параболы второго порядка: ![]() . Для определения параметров параболы по методу наименьших квадратов находят минимум функции
. Для определения параметров параболы по методу наименьших квадратов находят минимум функции
![]() .
.
При этом получают следующую систему нормальных уравнений:
![]()
![]() ;
;
![]() ;
;
![]() .
.
Первое уравнение почти полностью воспроизводит само уравнение параболы, второе уравнение старше первого на ![]() , третье - старше первого на
, третье - старше первого на ![]() .
.
Корреляционная таблица.
Парная таблица с большим числом наблюдений часто становится мало обозримой, и по ней неудобно вести расчеты. Поэтому для табличного изображения парной связи, решения уравнения регрессии и определения показателей тесноты связи используют корреляционную (двумерную) таблицу. В корреляционной таблице можно отобразить только парную связь, т. е. связь результативного признака с одним фактором. Она позволяет найти уравнение регрессии и вычислить линейный коэффициент корреляции. Само уравнение регрессии может иметь линейную, параболическую, гиперболическую, показательную и др. формы. При нахождении уравнения регрессии и линейного коэффициента по корреляционной таблице не теряется информация о связи, обусловленная усреднением данных. В корреляционной таблице связь между признаками выступает более рельефно, чем при рассмотрении средних значений факторного и результативного признаков. Однако, если обеспечивается возможность счета по каждой паре взаимосвязанных данных, необходимо ею воспользоваться и прибегать к корреляционной таблице лишь в отдельных случаях – при группировке данных.
Для составления корреляционной таблицы парной связи материал предварительно группируется по обоим признакам. Затем строится таблица, в которой по строкам откладываются группы одного (например, результативного) признака, а по столбцам размещаются группы другого (теперь факторного) признака. В клетках этой таблицы отмечается число единиц, имеющих определенную величину того и другого признаков. Итоги по строкам (![]() ) покажут число единиц в каждой группе результативного признака (если он размещен в строках). Итоги по колонкам (
) покажут число единиц в каждой группе результативного признака (если он размещен в строках). Итоги по колонкам (![]() ) покажут распределение факторного признака. В клетке, в которой итоги по строке сходятся с итогами по колонке, получаем число наблюдений:
) покажут распределение факторного признака. В клетке, в которой итоги по строке сходятся с итогами по колонке, получаем число наблюдений: ![]() .
.
Корреляционная зависимость задается таблицей:
Таблица 3
| х у |
|
| … |
|
|
|
|
|
| … |
|
|
|
|
|
| … |
|
|
| … | … | … | … | … | … |
|
|
|
| … |
|
|
|
|
|
| … |
|
|
Корреляционная таблица дает общее представление о направлении связи. Когда оба признака расположены в возрастающем порядке, числа предприятий в клетках сосредотачиваются в направлении диагонали слева направо, что указывает на прямую связь между признаками. Все числа предприятий сосредотачиваются в эллипсе, вытянутом по этой диагонали, называемом корреляционным эллипсом. Чем более сжат этот эллипс, тем кучнее частоты располагаются около его диагонали, тем теснее связь между признаками.
Эмпирическое корреляционное отношение.
Теснота или сила связи между двумя признаками может быть измерена показателем, называемым эмпирическим корреляционным отношением. Этот показатель назван эмпирическим, поскольку он может быть рассчитан на основе обычной группировки по факторному и результативному признаку, то есть на основе корреляционной таблицы. Эмпирическое корреляционное отношение получается из правила сложения дисперсий, согласно которому ![]() , где
, где ![]() - общая дисперсия;
- общая дисперсия; ![]() - межгрупповая дисперсия;
- межгрупповая дисперсия; ![]() - внутригрупповая (средняя из частных) дисперсия. Межгрупповая дисперсия является мерой колеблемости, обусловленной факторным признаком. Средняя из частных дисперсий является мерой колеблемости, обусловленной всеми остальными(кроме факторного) признаками. Тогда отношение
- внутригрупповая (средняя из частных) дисперсия. Межгрупповая дисперсия является мерой колеблемости, обусловленной факторным признаком. Средняя из частных дисперсий является мерой колеблемости, обусловленной всеми остальными(кроме факторного) признаками. Тогда отношение ![]() выражает долю колеблемости, возникающей за счет факторного признака, в общей колеблемости. Квадратный корень из этого отношения и называется эмпирическим корреляционным отношением:
выражает долю колеблемости, возникающей за счет факторного признака, в общей колеблемости. Квадратный корень из этого отношения и называется эмпирическим корреляционным отношением:
![]() .
.
Отсюда следует правило, что чем больше межгрупповая дисперсия, тем сильнее факторный признак влияет на вариации результативного признака. Составляющие отношения дисперсий вычисляются по данным корреляционной таблицы по следующим формулам:
![]() ;
; ![]() ,
,
где ![]() - частные средние;
- частные средние;
![]() - общая средняя;
- общая средняя;
![]() - итоги по признаку
- итоги по признаку ![]() ;
;
![]() - итоги по признаку
- итоги по признаку ![]() ;
;
![]() - число наблюдений.
- число наблюдений.
То же соотношение сохраняется и для условных значений ![]() , полученных числовым преобразованием
, полученных числовым преобразованием ![]() .
.
Само отношение дисперсий (подкоренное выражение) называется коэффициентом детерминации (оно равно также квадрату эмпирического корреляционного отношения). Эмпирическое корреляционное отношение изменяется в широких пределах (от 0 до 1). Если оно равно нулю, значит факторный признак на корреляционный не влияет. Если ![]() =1, значит, результативный признак полностью зависит от факторного. Если же эмпирическое корреляционное отношение представляет дробь, близкую единице, то говорят о тесной связи между факторным и результативным признаками. Если эта дробь мала (близка нулю), то говорят о слабой связи между ними.
=1, значит, результативный признак полностью зависит от факторного. Если же эмпирическое корреляционное отношение представляет дробь, близкую единице, то говорят о тесной связи между факторным и результативным признаками. Если эта дробь мала (близка нулю), то говорят о слабой связи между ними.
Коэффициент линейной корреляции и индекс корреляции.
Мерой тесноты связи между двумя статистически связанными признаками служит коэффициент линейной корреляции или просто коэффициент корреляции. Он имеет тот же смысл, что и эмпирическое корреляционное отношение, но может принимать как положительное, так и отрицательное значение. Коэффициент корреляции имеет строгое математическое выражение для линейной связи. Положительное значение будет указывать на прямую связь между признаками, отрицательное – на обратную.
Парный коэффициент корреляции в случае линейной формы связи вычисляют по формуле
![]() ,
,
а его выборочное значение – по формуле:
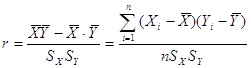
При малом числе наблюдений выборочный коэффициент корреляции удобно вычислять по следующей формуле:
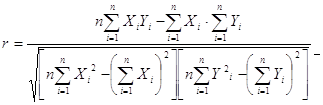
Величина коэффициента корреляции изменяется в интервале ![]() .
.
При ![]() между двумя переменными существует функциональная связь, при
между двумя переменными существует функциональная связь, при ![]() - прямая функциональная связь. Если
- прямая функциональная связь. Если ![]() , то значение Х и У в выборке некоррелированы; в случае, если система случайных величин
, то значение Х и У в выборке некоррелированы; в случае, если система случайных величин ![]() имеет двумерное нормальное распределение, то величины Х и У будут и независимыми.
имеет двумерное нормальное распределение, то величины Х и У будут и независимыми.
Если коэффициент корреляции находится в интервале ![]() , то между величинами Х и У существует обратная корреляционная связь. Это находит подтверждение и при визуальном анализе исходной информации. В этом случае отклонение величины У от среднего значения взяты с обратным знаком.
, то между величинами Х и У существует обратная корреляционная связь. Это находит подтверждение и при визуальном анализе исходной информации. В этом случае отклонение величины У от среднего значения взяты с обратным знаком.
Если каждая пара значений величин Х и У чаще всего одновременно оказывается выше (ниже) соответствующих средних значений, то между величинами существует прямая корреляционная связь и коэффициент корреляции находится в интервале ![]() .
.
Если же отклонение величины Х от среднего значения одинаково часто вызывают отклонения величины У вниз от среднего значения и при этом отклонения оказываются все время различными, то можно предполагать, что значение коэффициента корреляции стремится к нулю.
Следует отметить, что значение коэффициента корреляции не зависит от единиц измерения и выбора начала отсчета. Это означает, что если переменные Х и У уменьшить (увеличить) в К раз либо на одно и то же число С, то коэффициент корреляции не изменится.
Для упрощения расчетов меры тесноты корреляционной связи часто применяется индекс корреляционной связи, который определяется по следующим формулам:
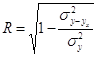 ,
, 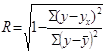 ,
,
где ![]() - остаточная дисперсия, характеризующая вариацию результативного признака под влиянием прочих неучтенных факторов.
- остаточная дисперсия, характеризующая вариацию результативного признака под влиянием прочих неучтенных факторов.
Множественная корреляция.
Множественная корреляция – зависимость результативного и двух или более факторных признаков, включенных в исследование. Показатель тесноты связи между результативным и двумя или более факторными признаками называется множественным или совокупным коэффициентом корреляции и обозначается R. Совокупный коэффициент предполагает наличие линейной связи между каждой парой признаков, которая может быть выражена при помощи парных коэффициентов корреляции. Если находится совокупная мера тесноты связи между результативным признаком (![]() ) и двумя факторными признаками(
) и двумя факторными признаками(![]() и
и ![]() ), то расчет совокупного коэффициента корреляции ведется по формуле:
), то расчет совокупного коэффициента корреляции ведется по формуле:
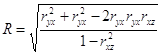 ,
,
Где подстрочные знаки обозначают, между какими признаками изучается парная связь.
В формулах расчетов парных коэффициентов корреляции изменяются лишь символы, обозначающие тот или иной фактор. Так, если коэффициент корреляции между ![]() и
и ![]() вычисляется по формуле
вычисляется по формуле ![]() , то коэффициент корреляции между
, то коэффициент корреляции между ![]() и
и ![]() вычисляется:
вычисляется: ![]() ; между
; между ![]() и
и ![]() - так:
- так:
![]()
Похожие работы
... запасов, дебиторской задолженности, денежных средств, ценных бумаг. Они служат исходными данными для расчета эффективности использования оборотных средств сельскохозяйственного предприятия. Ускорение оборачиваемости активов ведет к высвобождению, т.е. к экономии средств, сокращению в удельном выражении постоянных затрат, повышению ликвидности. [17 С.33] 2. Анализ экономической деятельности ...
... оборотных средств за счет расширения сфер деятельности предпринимателя Постоянное расширение сфер предпринимательской деятельности является одной из мер повышения эффективности использования оборотных средств, а так же насущной необходимостью. Существует поговорка, что «в бизнесе, для того чтобы стоять на месте нужно постоянно бежать». Расширение возможно как в сторону увеличения уже ...
... его непрерывность и бесперебойную работу предприятия. Поэтому в следующей части работы рассмотрим обеспеченность и эффективность использования оборотных средств сельскохозяйственного предприятия ООО «Россия». 2 Анализ управления оборотным капиталом на сельскохозяйственном предприятии ООО«Россия» 2.1 Организационно-экономическая характеристика предприятия Колхоз «Россия» (с 2007 года ООО ...
... в пределах от 4796,9 до 4825,5 ц. Вычислим среднюю ошибку аппроксимации: Следовательно, точность прогноза - высокая. Заключение Проведя комплексный статистико-экономический анализ эффективности производства продукции животноводства по 30 предприятиям Ярославской области, можно сделать вывод, что не все из рассмотренных хозяйств являются эффективными. Наиболее главной целью любого ...

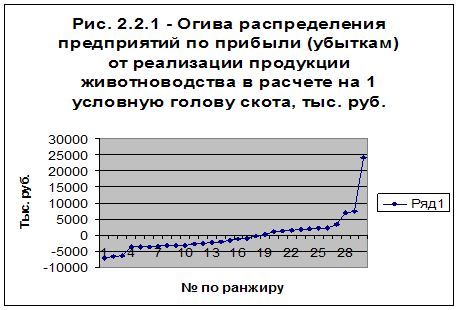
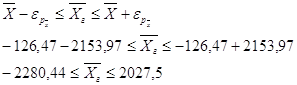
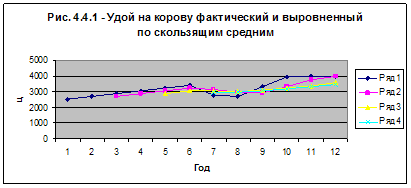
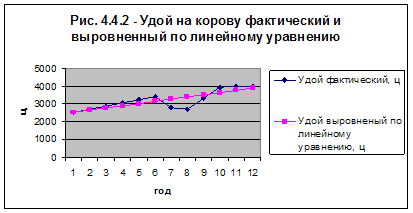
0 комментариев