Навигация
Выборочный метод анализа
2.1 Выборочный метод анализа.
Выборочное наблюдение — это такой вид несплошного наблюдения, при котором отбор подлежащих обследованию единиц осуществляется в случайном порядке, отобранная часть изучается, а результаты распространяются на всю исходную совокупность. Наблюдение организуется таким образом, что эта часть отобранных единиц в уменьшенном масштабе репрезентирует (представляет) всю совокупность. [15]
В данной работе мы будем использовать механическую бесповторную выборку. Для этого предварительно расположим единицы совокупности (регионы страны) в алфавитном порядке, не затрагивая при этом показатели, связанные с изучаемым свойством. После этого отберем заданное число единиц (n) механически, через определенный интервал. При этом размер интервала в генеральной совокупности равен обратному значению доли выборки.
Доля выборки есть отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности: ![]() .
.
При бесповторной выборке единица совокупности, попавшая в выборку, в генеральную совокупность не возвращается и в дальнейшем в выборке не участвует; т. е. последующую выборку делают из генеральной совокупности уже без отобранных ранее единиц («отбор по схеме невозвращенного шара»). Таким образом, при бесповторной выборке численность единиц генеральной совокупности сокращается в процессе исследования.
Необходимое число единиц выборочной совокупности найдем по формуле: 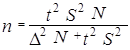 , где N = 79, t = 2 (нормированное отклонение — «коэффициент доверия», зависящий от вероятности, с которой гарантируется предельная ошибка выборки), а, следовательно, Ф(t) = 0,954. Предельная ошибка выборки (
, где N = 79, t = 2 (нормированное отклонение — «коэффициент доверия», зависящий от вероятности, с которой гарантируется предельная ошибка выборки), а, следовательно, Ф(t) = 0,954. Предельная ошибка выборки (![]() ) отвечает на вопрос о точности выборки с определенной вероятностью, значение которой определяется коэффициентом t (в практических расчетах, как правило, заданная вероятность не должна быть менее 0,95).
) отвечает на вопрос о точности выборки с определенной вероятностью, значение которой определяется коэффициентом t (в практических расчетах, как правило, заданная вероятность не должна быть менее 0,95).
Зададим ![]() = 38 тыс. чел.
= 38 тыс. чел.
Для расчета объема выборки нужно знать дисперсию. Для ее определения надо провести специальное выборочное обследование небольшого объема. В нашем случае отберем регионы со значением среднегодовой численности занятого населения от 100 до 500 тыс. человек, поскольку значения генеральной совокупности сильно варьируют и в противном случае n будет равным N. Все расчеты будем производить в электронной таблице Excel с целью снижения трудоемкости работы. В итоге SІ = 12779935312.
Подставив все полученные значения в формулу, получим:
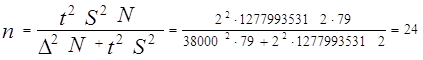 .
.
Обратное значение доли выборки: ![]() .
.
Чтобы в выборку попало 24 региона, отберем из списка (который мы расположили в алфавитном порядке), начиная с первого региона, 9 регионов, отсчитывая каждый 4-й регион и затем 14 регионов, отсчитывая каждый 3-й регион. Схема выборки показана в приложении 1.
2.2 Сводка и группировка данных.
Статистическая сводка – это процесс обобщения данных статистического наблюдения, которая обеспечивает получение статистических показателей как сводных признаков массового явления. Важнейшим элементом и научной основой сводки является группировка.
Статистическая группировка – это метод расчленения сложного массового явления на существенно-различные группы, однородных по какому-либо признаку, с целью всесторонней характеристики состояния, развития и взаимосвязи. [14]
Для выделения типов исследуемых явлений, структуры совокупности по нескольким признакам и при анализе взаимосвязей между признаками применяются комбинационные группировки. Особенно важное значение они имеют в тех случаях, когда влияние одного факторного признака на результативный затушевывается влиянием другого фактора. Группировка по нескольким признакам позволяет не только выявить влияние каждого из факторов отдельно, но и вскрывает зависимость между факторами.
Группировка, в задачу которой входит выявление и характеристика взаимосвязи между признаками изучаемых явлений, называется аналитической. Она обычно проводится по признаку, который является определяющим, причинным в данной зависимости. Такой признак называется факторным. Признаки группировки, которые обусловливаются факторным признаком, называется результативными. В нашем случае среднегодовая численность занятого населения является результативным признаком (У), а ВРП на душу населения, численность экономически активного населения, численность мужчин в трудоспособном возрасте – факторными (Х).
Аналитические группировки применяются для выявления и изучения взаимосвязи между явлениями и их различными признаками. В зависимости от количества изучаемых признаков (образованные по одному признаку – простые; образованные группы по одному признаку и делящиеся на группы по второму признаку и т.д. - комбинационные). Выявим зависимость между среднегодовой численность занятого населения (данные указаны в приложении 2), численностью экономически активного населения (приложение 3), численностью мужчин в трудоспособном возрасте (приложение 4) и ВРП на душу населения (приложение 5), используя метод аналитической группировки.
Чтобы показать наиболее реальную картину влияния факторов на занятость населения, будем группировать не объемные показатели факторных признаков, а их доли от общей численности постоянного населения.
Построив ранжированный ряд по каждому факторному признаку, определим интервалы групп, используя шаг по формуле:
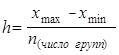 ,
,
где ![]() и
и ![]() - наибольшее и наименьшее значение изучаемого группировочного признака. Для малых выборочных совокупностей (n < 30) необходимо брать небольшое число групп. Тогда шаг для группировки регионов по уровню численности экономически активного населения в числе постоянного населения равен:
- наибольшее и наименьшее значение изучаемого группировочного признака. Для малых выборочных совокупностей (n < 30) необходимо брать небольшое число групп. Тогда шаг для группировки регионов по уровню численности экономически активного населения в числе постоянного населения равен:
![]()
Для группировки доли численности мужчин в трудоспособном возрасте в числе постоянного населения:
![]()
Для группировки ВРП на душу населения:
![]() руб.
руб.
Вспомогательная группировочная таблица приведена в приложении 7. Анализируя данную таблицу, можно сказать, что в Российской Федерации регионы с низким уровнем экономической активности населения (35,21-43,02 %) имеют в свою очередь низкий уровень численности мужчин в трудоспособном возрасте в числе постоянного населения (28,84-31,61 %), а также низкий показатель ВРП на душу населения (29903,7-203345,07 руб.), что приводит к самой низкой доли среднегодовой численности занятого населения в числе постоянного населения (в среднем 23,8%). Таких регионов в выборочной совокупности всего 2 из 24-х.
Во вторую группу входит 9 регионов России. В данной группе присутствуют регионы с низким и средним уровнем численности мужчин в трудоспособном возрасте от общей численности постоянного населения, а также с низким показателем ВРП на душу населения, аналогично предыдущей группе. При этом наблюдается наиболее высокая доля среднегодовой численности занятого населения в общей численности постоянного населения (в среднем 43,75 %).
"Золотую" середину по всей рассматриваемой совокупности занимают регионы с более высоким уровнем экономической активности населения по сравнению с двумя предыдущими группами (50,82-58,62 %). Таких регионов 13. В данной группе присутствуют как регионы с низким и средним, так и с высоким уровнем численности мужчин в трудоспособном возрасте от общей численности постоянного населения, а также наблюдается более высокий показатель ВРП на душу населения (в среднем 199729,8 рублей). При этом наибольшая доля среднегодовой численности занятого населения в общей численности постоянного населения отмечается у регионов с высоким показателем ВРП на душу населения.
На основании вспомогательной группировочной таблицы найдем средние уровни показателей и определим их зависимость (таблица 2.2.1).
Таблица 2.2.1
Зависимость среднегодовой численности занятого населения
от взаимодействия численности экономически активного населения,
численности мужчин в трудоспособном возрасте
и ВРП на душу населения
| Группы регионов по уровню численности экономически активного населения в числе постоянного населения, % | Число регионов в группе | Средние уровни | |||
| Доля численности экономически активного населения в числе постоянного населения | Доля численности мужчин в трудоспособном возрасте в числе постоянного населения | ВРП на душу населения, руб. | Доля среднегодовой численности занятого населения в числе постоянного населения | ||
| I. 35,21-43,02 | 2 | 0,3872 | 0,2930 | 46 794,9 | 0,2380 |
| II. 43,02-50,82 | 9 | 0,4912 | 0,3188 | 113 880,2 | 0,4375 |
| III. 50,82-58,62 | 13 | 0,5405 | 0,3322 | 199 729,8 | 0,4881 |
| Итого по регионам | 24 | 0,5092 | 0,3239 | 154 791,6 | 0,4483 |
Анализ данных таблицы 2.2.1 свидетельствует о наличии прямой связи между среднегодовой численностью занятого населения, численностью экономически активного населения, численностью мужчин в трудоспособном возрасте и ВРП на душу населения. Т.е. с увеличением численности экономически активного населения, с увеличением численности мужчин в трудоспособном возрасте, а также с увеличением ВРП на душу населения растет среднегодовая численность занятого населения.
Можно также сказать, что при увеличении доли численности экономически активного населения в числе постоянного населения число регионов увеличивается, т.е. чаще всего преобладает доля численности экономически активного населения в числе постоянного населения от 50,82 до 58,62 %.
2.3 Ряд распределения регионов по среднегодовой численности занятого населения и его характеристика. Проверка гипотезы о законе распределения регионов по среднегодовой численности занятого населения.
Ряд распределения – простейшая группировка, представляющая собой распределение численности единиц совокупности по какому-либо признаку. Он характеризует состав (структуру) изучаемого явления, позволяет судить об однородности совокупности, закономерности распределения и границах варьирования единиц совокупности. [14]
Составим вариационный интервальный ряд распределения (когда признак х – принимает значение интервала (от… до…)) регионов по среднегодовой численности занятого населения, данные которого занесем в таблицу 2.3.1.
На первом этапе анализа трудовых ресурсов в какой-либо совокупности необходимо получить представление о ее вариации, изменчивости, а затем установить причины изменения и степени влияния факторов. Вариация, представляющая собой различие индивидуальных значений единиц совокупности, есть необходимое условие существования и развития массовых явлений. В жизни общества, как и в природе, каждой массовой совокупности, массовому процессу присуща некоторая специфическая мера вариации ее элементов, при которой данный процесс протекает оптимально. Для изучения вариации трудовых ресурсов используют ряд приемов: построение рядов распределения, расчет обобщающих показателей вариации, графическое изображение уровней, расчет показателей динамики и сравнения.Ранжированный и интервальный ряды распределения строят для совокупности рассредоточенных в пространстве, сосуществующих в данный момент или период времени единиц. Ряд распределения показывает распределение единиц совокупности по какому-либо признаку в пространстве. Ряд распределения состоит из двух элементов (х – значения признака, f – частоты, веса).
Определим шаг интервала: 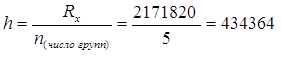 ,
,
где n нашли по формуле Стерджесса: n = 1+3,3221lgN = 1+3,3221lg79 ≈ 5;
![]() чел. - размах вариации, показывающий границы, в пределах которых изменяется среднегодовая численность занятого населения по регионам в Российской Федерации.
чел. - размах вариации, показывающий границы, в пределах которых изменяется среднегодовая численность занятого населения по регионам в Российской Федерации.
Но поскольку в последних двух группах локальные частоты слишком малы (f4 = 1 и f 5= 2), то их следует объединить, тогда получится 4 группы регионов.
Таблица 2.3.1
Исходные данные распределения регионов России
по среднегодовой численности занятого населения
| Группы регионов по среднегодовой численности занятого населения, чел., х | Число регионов в группе,
|
|
| Кумулятивные частоты |
|
|
|
| 65510-499874 | 11 | 282692 | 3109612 | 11 | -425314,75 | 180892636568 | 1989819002248 |
| 499874-934238 | 7 | 717056 | 5019392 | 18 | 9049,25 | 81888926 | 573222482 |
| 934238-1368602 | 3 | 1151420 | 3454260 | 21 | 443413,25 | 196615310276 | 589845930828 |
| 1368602-2237330 | 3 | 1802966 | 5408898 | 24 |
| 1198935759161 | 3596807277483 |
| Итого по группам | 24 | 708006,75 | 16992162 | - | - | 1576525594931 | 6177045433041 |
По данным таблицы 2.3.1 видно, что в России наибольший удельный вес занимают регионы с небольшой среднегодовой численностью занятого населения (65510-499874 чел.). Таких регионов 11 из 24. Самой высокой численностью занятого населения отличается Краснодарский край – 2237330 чел.
Используя исходные данные таблицы 2.3.1, дадим оценку распределения регионов по средней величине численности занятого населения, используя структурные средние. Данные средней величины позволяют устранить влияние аномальных значений показателя.
Определим показатель центра распределения: 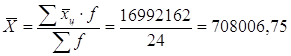 чел.
чел.
Т.е. среднее значение численности занятого населения составляет 708007 чел.
Найдем единицы совокупности, которые расположены в медианном, квартельном и децильном интервалах:
![]()
Мода - это то, что чаще всего мы наблюдаем, т.е. это значение признака, которое чаще всего встречается у единиц совокупности, частота встреч определяется по величине f.
Для дискретных рядов мода – это вариант с наибольшей частотой, для интервальных рядов распределения мода рассчитывается по следующей формуле:
![]() чел.
чел.
где М0 – мода; х0 – начало (нижняя граница) модального интервала (с наибольшей численностью);
h – величина модального интервала;
f1 – частота интервала, предшествующего модальному;
f2 – частота модального интервала;
f3– частота интервала, следующего за модальным.
Значит, в нашей совокупности регионов наиболее часто встречаются регионы, имеющие среднегодовую численность занятого населения 384044 чел.
Графическое определение моды показано на рисунке 1.
Величина моды и медианы, как правило, отличается от величины средней, совпадая с ней только в случае симметрии вариационного ряда. Мода и медиана по-разному характеризуют совокупность. Мода определяет непосредственно размер признака, свойственный хотя и значительной части, но все же не всей совокупности. Мода по своему обобщающему значению менее точна по сравнению со средней арифметической, характеризующей совокупность в целом с учетом всех без исключения элементов совокупности.
Медианой является значение элемента, который больше или равен и одновременно меньше или равен половине остальных элементов ряда распределения. Медиана делит ряд на две равные части. Она не зависит ни от амплитуды колебаний ряда, ни от распределения частот в пределах двух равных частей ряда, поэтому ее применение позволяет получить более точные результаты, чем при использовании других форм средних. Медиану определяют по формуле:
![]() чел.
чел.
Таким образом, 50 % регионов страны имеют среднегодовую численность занятого населения менее 561926 человек и, соответственно, остальные 50 % - более 561926 человек.
На четыре равные части изучаемую совокупность делит квартель, который находится по формуле:
![]() чел.
чел.
![]() чел.
чел.
Отсюда следует, что 25 % регионов страны имеют менее 302436 человек и 25 % - более 776288 человек. Более точные данные можно получить с помощью дециля:
![]() чел.
чел.
![]() чел.
чел.
Полученные результаты показывают, что среднегодовая численность занятого населения в 10 % регионов России составляет менее 160280 человек, другие 10 % - более 1542347 человек.
![]()
|
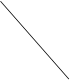
Рис. 1. Гистограмма локальных частот
![]() чел. - квартельный размах, который показывает, что изменение среднегодовой численности занятого населения по регионам, находящимся в центре изучаемой совокупности, варьирует в пределах 473852 человек.
чел. - квартельный размах, который показывает, что изменение среднегодовой численности занятого населения по регионам, находящимся в центре изучаемой совокупности, варьирует в пределах 473852 человек.
Для оценки вариации у совокупности единиц в целом рассчитывают среднее линейное отклонение и дисперсию (средний квадрат отклонений численности занятого населения от ее средней величины): [14]
![]()
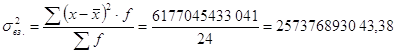
Для удобства описания данных рассчитывают среднеквадратическое отклонение:
![]() чел.
чел.
То есть по Российской Федерации численность занятого населения по регионам варьирует в среднем на ± 507323 человека от среднего уровня (708007 чел.). Тогда коэффициент вариации составит:
![]() или 71,66 %, что говорит о сильном варьировании численности занятого населения по регионам страны.
или 71,66 %, что говорит о сильном варьировании численности занятого населения по регионам страны.
Проверим гипотезу о законе распределения регионов России по среднегодовой численности занятого населения. Для этого на основании построенной гистограммы локальных частот (рис. 1) выдвинем основную (нулевую) гипотезу: Н0: Х в генеральной совокупности (т.е. по всей России) имеет показательное распределение.
Соответственно, альтернативная ей гипотеза:
Н1: Х в генеральной совокупности не имеет показательного закона распределения.
Х - распределение регионов по среднегодовой численности занятого населения, чел.
Для удобства расчетов теоретических частот и наблюдаемого значения статистического критерия χ² вычисления будем проводить в таблице 2.3.2.
Таблица 2.3.2
Исходные данные для проверки гипотезы о законе распределения регионов России по среднегодовой численности занятого населения
| Интервал хi – xi+1 | Число регионов в группе,
|
| pi | ni' = f·pi |
|
|
| 65510-499874 | 11 | 282692 | 0,4179 | 10,0296 | 0,9417 | 0,0939 |
| 499874-934238 | 7 | 717056 | 0,2263 | 5,4312 | 2,4611 | 0,4531 |
| 934238-1368602 | 3 | 1151420 | 0,1226 | 2,9424 | 0,0033 | 0,0011 |
| 1368602-2237330 | 3 | 1802966 | 0,1023 | 2,4552 | 0,2968 | 0,1209 |
| Итого | 24 | 708006,75 | - | - | - | 0,6690 |
Найдем оценку параметра предполагаемого показательного распределения: ![]()
Вычислим вероятности попадания в каждый из интервалов:
![]()
![]()
![]()
![]()
![]()
Найдем теоретические частоты: ni' = f·pi=24·pi
n1' =24·0,4179 = 10,0296n3' =24·0,1226 = 2,9424
n2' =24·0,2263 = 5,4312 n4' =24·0,1023 = 2,4552
После проведения сравнения теоретических и локальных частот вычисляем: 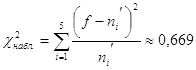
![]() (α=0,05; k=S-r-1=3-1-1=1) = 3,8 (по таблице критических точек распределения χ², которая приведена в приложении 8), где r = 1, т.к. показательный закон распределения имеет 1 параметр (λ).
(α=0,05; k=S-r-1=3-1-1=1) = 3,8 (по таблице критических точек распределения χ², которая приведена в приложении 8), где r = 1, т.к. показательный закон распределения имеет 1 параметр (λ).
S = 3 (число групп выборки), т.к. малочисленные частоты (f < 5) объединили.
Ищут всегда правостороннюю критическую область (рис. 2).
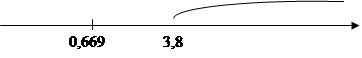 | |||
Рис. 2. Нахождение критического значения статистики
![]()
критической области Þ нет оснований отвергать гипотезу Н0. Т.е. регионы по среднегодовой численности занятого населения в России имеют показательное распределение:
Похожие работы
... показателей эффективности использования фондов снизился на 9,5%; 14. Уровень рентабельности вырос на 0,6%; 15. норма рентабельности снизилась на 28,6%. Глава 3 Статистический анализ трудовых ресурсов 3.1 Статистический анализ и использование трудовых ресурсов в Райпо Трудовые ресурсы – это часть населения обоего пола в трудоспособном возрасте за вычетом неработающих, нетрудоспособных и ...
... существования общества. Статистика труда тесно связана с другими областями статистики: статистической производственных отраслей, системой национальных счетов, демографией статистической культуры, здравоохранения и другие. 2. Статистический анализ наличия, состава и использования трудовых ресурсов в хозяйстве 2.1 Монографическое описание хозяйства Сельскохозяйственный производственный ...
... , нормативная, проектная (сметная), прогнозируемая; по масштабам охватываемого объекта - цех, предприятие, группа предприятий, отрасль, промышленность и т.п. [9;162] 2. Статистико-экономический анализ себестоимости продукции 2.1. Характеристика структуры затрат на производство На основе группировки затрат по экономическим элементам можно охарактеризовать структуру себестоимости продукции ...
... сил (неолитическая, промышленная, научно-техническая) знаменуют качественные этапы повышения производительности труда. 1.2 Показатели производительности труда Статистика сельского хозяйства изучает уровень и динамику производительности труда. Выявляется и измеряется влияние важнейших природно-экономических факторов на уровень производительности труда. Для характеристики уровня и динамики ...
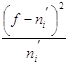

0 комментариев