Навигация
Задача прогнозирования возможных значений результативного признака при задаваемых значениях факторных признаков
3. Задача прогнозирования возможных значений результативного признака при задаваемых значениях факторных признаков.
Такая задача решается путем подстановки ожидаемых, или планируемых, или возможных значений факторных признаков в уравнение связи и вычисления ожидаемых значений результативного признака.
Приходится решать и обратную задачу: вычисление необходимых значений факторных признаков для обеспечения планового или желаемого значения результативного признака в среднем по совокупности. Эта задача обычно не имеет единственного решения в рамках данного метода и должна дополняться постановкой и решением оптимизационной задачи на нахождение наилучшего из возможных вариантов ее решения (например, варианта, позволяющего достичь требуемого результата с минимальными затратами).
4. Задача подготовки данных, необходимых в качестве исходных для решения оптимизационных задач. Например, для нахождения оптимальной структуры производства в районе на перспективу исходная информация должна включать показатели производительности на предприятиях разных отраслей и форм собственности. В свою очередь, эти показатели могут быть получены на основе корреляционно-регрессионной модели либо на основании тренда динамического ряда (а тренд - это тоже уравнение регрессии).
При решении каждой из названных задач нужно учитывать особенности и ограничения корреляционно-регрессионного метода. Всякий раз необходимо специально обосновать возможность причинной интерпретации уравнения как объясняющего связь между вариацией фактора и результата. Трудно обеспечить раздельную оценку влияния каждого из факторов. В этом отношении корреляционные методы глубоко противоречивы. С одной стороны, их идеал - измерение чистого влияния каждого фактора. С другой стороны, такое измерение возможно при отсутствии связи между факторами и случайной вариации признаков. А тогда связь является функциональной, и корреляционные методы анализа излишни. В реальных системах связь всегда имеет статистический характер, и тогда идеал методов корреляции становится недостижимым. Но это не значит, что эти методы не нужны.
Данное противоречие означает попросту недостижимость абсолютной истины в познании реальных связей. Приближенный характер любых результатов корреляционно-регрессионного анализа не является поводом для отрицания их полезности. Всякая научная истина — относительна. Забыть об этом и абсолютизировать параметры регрессионных уравнений, меры корреляции было бы ошибкой, так же как и отказаться от использования этих мер.
Поскольку корреляционная связь является статистической, первым условием возможности ее изучения является общее условие всякого статистического исследования: наличие данных по достаточно большой совокупности явлений. По отдельным явлениям можно получить совершенно превратное представление о связи признаков, ибо в каждом отдельном явлении значения признаков кроме закономерной составляющей имеют случайное отклонение (вариацию). Например, сравнивая два хозяйства, одно из которых имеет лучшее качество почв, по уровню урожайности, можно обнаружить, что урожайность выше в хозяйстве с худшими почвами. Ведь урожайность зависит от сотен факторов и при том же самом качестве почв может быть и выше, и ниже. Но если сравнивать большое число хозяйств с лучшими почвами и большое число - с худшими, то средняя урожайность в первой группе окажется выше и станет возможным измерить достаточно точно параметры корреляционной связи.
Какое именно число явлений достаточно для анализа корреляционной и вообще статистической связи, зависит от цели анализа, требуемой точности и надежности параметров связи, от числа факторов, корреляция с которыми изучается. Обычно считают, что число наблюдений должно быть не менее чем в 5-6, а лучше - не менее чем в 10 раз больше числа факторов. Еще лучше, если число наблюдений в несколько десятков или в сотни раз больше числа факторов, тогда закон больших чисел, действуя в полную силу, обеспечивает эффективное взаимопогашение случайных отклонений от закономерного характера связи признаков.
Вторым условием закономерного проявления корреляционной связи служит условие, обеспечивающее надежное выражение закономерности в средней величине. Кроме уже указанного большого числа единиц совокупности для этого необходима достаточная качественная однородность совокупности. Нарушение этого условия может извратить параметры корреляции. Например, в массе зерновых хозяйств уровень продукции с гектара растет по мере концентрации площадей, т.е. он выше в крупных хозяйствах. В массе овощных и овоще-молочных хозяйств (пригородный тип) наблюдается та же прямая связь уровня продукции с размером хозяйства. Но если соединить в общую неоднородную совокупность те и другие хозяйства, то связь уровня продукции с размером площади пашни (или посевной площади) получится обратной. Причина в том, что овощные и овоще-молочные хозяйства, имея меньшую площадь, чем зерновые, производят больше продукции с гектара ввиду большей интенсивности производства в данных отраслях, чем в производстве зерна.
Иногда как условие корреляционного анализа выдвигают необходимость подчинения распределения совокупности по результативному и факторным признакам нормальному закону распределения вероятностей. Это условие связано с применением метода наименьших квадратов при расчете параметров корреляции: только при нормальном распределении метод наименьших квадратов дает оценку параметров, отвечающую принципам максимального правдоподобия. На практике эта предпосылка чаще всего выполняется приближенно, но и тогда метод наименьших квадратов дает неплохие результаты.
Однако при значительном отклонении распределений признаков от нормального закона нельзя оценивать надежность выборочного коэффициента корреляции, используя параметры нормального распределения вероятностей или распределения Стьюдента.
Еще одним спорным вопросом является допустимость применения корреляционного анализа к функционально связанным признакам. Можно ли, например, построить уравнение корреляционной зависимости размеров выручки от продажи картофеля, от объема продажи и цены? Ведь произведение объема продажи и цены равно выручке в каждом отдельном случае. Как правило, к таким жестко Детерминированным связям применяют только индексный метод анализа. Однако на этот вопрос можно взглянуть и с другой точки зрения. При индексном анализе выручки предполагается, что количество проданного картофеля и его цена независимы друг от друга, потому-то и допустима абстракция от изменения одного фактора при измерении влияния другого, как это принято в индексном методе. В реальности количество и цена не являются вполне независимыми друг от друга.
Корреляционно-регрессионный анализ учитывает межфакторные связи, следовательно, дает нам более полное измерение роли каждого фактора: прямое, непосредственное его влияние на результативный признак; косвенное влияние фактора через его влияние на другие факторы; влияние всех факторов на результативный признак. Если связь между факторами несущественна, индексным анализом можно ограничиться. В противном случае его полезно дополнить корреляционно-регрессионным измерением влияния факторов, даже если они функционально связаны с результативным признаком.
4.2 Построение однофакторной корреляционной модели зависимости себестоимости 1 ц. от фактора (Х- урожайность зерна, (сахарной свеклы, подсолнечника), Х – производственных затрат)
В качестве предмета исследования в этом разделе выберем зависимость себестоимости 1 ц. от фактора (Х- урожайность зерна, (сахарной свеклы, подсолнечника), Х – производственных затрат).
Таблица 8. Исходные и расчетные данные построения корреляционно – регрессионной модели себестоимости
| Номер предпиятия | Себестоимость 1 ц. продукции, руб. | Факторный признак | х2 | ух | у2 | ух |
| 1 | 119.64 | 15.4 | 237.16 | 1842.46 | 14313.73 | -38.25 |
| 2 | 161.92 | 27.9 | 778.41 | 4517.57 | 26218.09 | -103.25 |
| 3 | 237.9 | 30.2 | 912.04 | 7184.58 | 56596.41 | -115.21 |
| 4 | 163.82 | 19.9 | 396.01 | 3260.02 | 26836.99 | -61.65 |
| 5 | 148.38 | 29.4 | 864.36 | 4362.37 | 22016.62 | -111.05 |
| 6 | 193 | 15.8 | 249.64 | 3049.40 | 37249.00 | -40.33 |
| 7 | 193 | 20.3 | 412.09 | 3917.90 | 37249.00 | -63.73 |
| 8 | 184.72 | 19.8 | 392.04 | 3657.46 | 34121.48 | -61.13 |
| 9 | 193.39 | 20 | 400 | 3867.80 | 37399.69 | -62.17 |
| 10 | 165.22 | 17.7 | 313.29 | 2924.39 | 27297.65 | -50.21 |
| 11 | 152.09 | 21.5 | 462.25 | 3269.94 | 23131.37 | -69.97 |
| 12 | 258.3 | 37.7 | 1421.29 | 9737.91 | 66718.89 | -154.21 |
| 13 | 179.97 | 30.5 | 930.25 | 5489.09 | 32389.20 | -116.77 |
| 14 | 54.63 | 20.2 | 408.04 | 1103.53 | 2984.44 | -63.21 |
| 15 | 120.36 | 20.7 | 428.49 | 2491.45 | 14486.53 | -65.81 |
| 16 | 153.63 | 21.8 | 475.24 | 3349.13 | 23602.18 | -71.53 |
| 17 | 99.73 | 18.9 | 357.21 | 1884.90 | 9946.07 | -56.45 |
| 18 | 119.92 | 17 | 289 | 2038.64 | 14380.81 | -46.57 |
| 19 | 187.91 | 26.6 | 707.56 | 4998.41 | 35310.17 | -96.49 |
| 20 | 103.96 | 17.8 | 316.84 | 1850.49 | 10807.68 | -50.73 |
| 21 | 76.24 | 13.2 | 174.24 | 1006.37 | 5812.54 | -26.81 |
| Итого | 3267.73 | 462.3 | 10925.45 | 75803.79 | 558868.53 | -1525.53 |
Определим параметры уравнения регрессии:
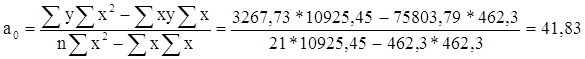
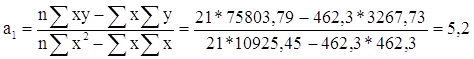
Уравнение регрессии:
yх=a0+a1*x
yх=41,83 – 5,2x.
Теснота связи:
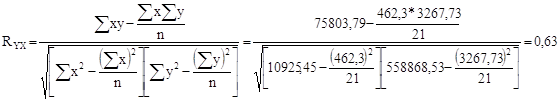
D = 0,3969
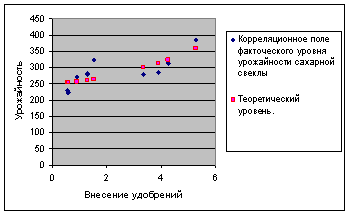
Таким образом, связь между урожайностью и себестоимостью по шкале Чэддека достаточная или средняя. Оценка линейного коэффициента корреляции показывает, что связь прямая, т. е. с увеличением урожайности увеличивается и себестоимость 1ц. зерна (сахарной свеклы, подсолнечника).
Выводы и предложения
В ходе решения задач курсовой работы получены следующие результаты:
Себестоимость и производственные затраты — важнейшие результативные показатели растениеводства и сельскохозяйственного производства в целом. Уровень себестоимости отражает воздействие экономических и приходных условий, в которых осуществляется сельскохозяйственное производство, и качество организационно-хозяйственной деятельности каждого предприятия.
Производственные затраты характеризуют общий объем затрат производства продукции данной культуры, а себестоимость — стоимостную оценку этой культуры в конкретных условиях ее возделывания.
Динамика производственных затрат характеризуется общим подъемом на 20,3% за исследуемый период. При этом как цепные так и базисные показатели темпов прироста имеют преимущественно положительное значение, что позволяет характеризовать динамику как общее подъем производственных затрат.
Себестоимость зерна (сахарной свеклы, подсолнечника) имеет также тенденцию к подъёму, однако не настолько большую как производственные затраты и составляет за исследуемый период лишь 6,8%.
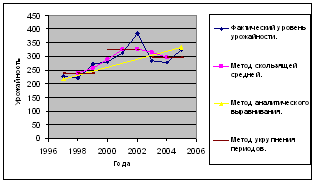
С помощью методов выравнивания выявлена общая тенденция подъема себестоимости зерна (сахарной свеклы, подсолнечника) за исследуемый период.
Динамика себестоимости зерна (сахарной свеклы, подсолнечника) за исследуемый период носит устойчивую тенденцию к повышению, при этом локальная колебимость признака, имеющая место в 2000, 2003 и 2004 годах не оказала существенного влияния на общие результаты выравнивания, а значит, является статистически малозначимой.
В статистике под индексом понимается относительный показатель который выражает соотношение величин какого-либо явления во времени, в пространстве или дает сравнение фактических данных с любым эталоном (план, прогноз, норматив и т.д.).
Все экономические индексы можно классифицировать по следующим признакам:
• степень охвата явления;
• база сравнения;
• вид весов (соизмерителя);
• форма построения;
• характер объекта исследования:
• объект исследования;
• состав явления;
• период исчисления.
Средняя себестоимость 1 ц. зерна (сахарной свеклы, подсолнечника) в отчетном году по сравнению с базисным увеличилась на 44,31 или на 40 %.
За счет увеличения себестоимости 1 ц. продукции в отдельных хозяйствах производственные затраты увеличились на ![]() ц или на 37 %. За счет улучшения структуры произведенной продукции производственные затраты увеличилась на
ц или на 37 %. За счет улучшения структуры произведенной продукции производственные затраты увеличилась на ![]() ц или на 2 %. За счет уменьшения количества произведенной продукции производственные затраты уменьшились на 1542393,94 ц. или на 3 %
ц или на 2 %. За счет уменьшения количества произведенной продукции производственные затраты уменьшились на 1542393,94 ц. или на 3 %
На объем производственных затрат положительно повлияли повышение себестоимости в отдельных хозяйствах и отрицательно - уменьшение количества произведенной продукции, положительно повлияло улучшение структуры произведенной продукции. В результате производственные затраты в отчетном году по сравнению с базисным увеличились на 25044373 ц. или на 37 %.
Группировка — это распределение единиц по группам в соответствии со следующим принципом: различия между единицами, отнесенными к одной группе, должны быть меньше, чем между единицами, отнесенными к разным группам.
Различия в целевом назначении группировки выражаются в существующей в отечественной статистике классификации группировок: типологические, структурные, аналитические.
Корреляционно-регрессионный анализ учитывает межфакторные связи, следовательно, дает нам более полное измерение роли каждого фактора: прямое, непосредственное его влияние на результативный признак; косвенное влияние фактора через его влияние на другие факторы; влияние всех факторов на результативный признак. Если связь между факторами несущественна, индексным анализом можно ограничиться. В противном случае его полезно дополнить корреляционно-регрессионным измерением влияния факторов, даже если они функционально связаны с результативным признаком.
С помощью корреляционно-регрессионного исследования выявлено, что связь между себестоимостью и урожайностью средняя. Оценка линейного коэффициента корреляции показывает, что связь прямая, т. е. с увеличением урожайности увеличивается и себестоимость 1ц. зерна (сахарной свеклы, подсолнечника).
Список литературы
1. Адамов В.К. Факторный индексный анализ (Методология и проблемы). ML: Статистика. 2005.- 200 с.
2. Альбом наглядных пособий по общей теории статистики: Учеб. пособие. М.: Финансы и статистика, 2005.- 80 с.
3. Анализ финансово-экономической деятельности предприятия: Учеб. Пособие для ВУЗов/под ред. Любушина Н.П. –М.: ИНИТИ – ДАНА, 2005.- 471с.
4. Баканов М.И., Шеремет А.Д. Теория анализа хозяйственной деятельности Учебник, 3-е переработанное и дополненное издание: М.: Финансы и статистика. 2007. – 489 с.
5. Вучков И. и др. Прикладной линейный регрессионный анализ / Пер. с болг. И. Вучков, Л. Бояджиева, Е. Солжов. М: Финансы и статистика, 2008.- 239 с.
6. Долгушевский Ф.Г., Христич А.Г. Сельскохозяйственная статистика с основами экономической статистики. М.: Статистика, 2006. – 311 с
7. Елисеева И.И. Общая теория статистики. М. Финансы и статистика. 2007. – 287 с
8. Емельянов A.M. Экономика сельского хозяйства М.: Экономика. 2007. – 290 с.
9. Ефимова М.Р., Рябцев В.М. Общая теория статистики: Учебник. М.: Финансы и статистика, 2005.- 303 с.
10. Кравченко Л.И. Анализ финансового состояния предприятия. М.: ЮНИТИ. 2006. – 450 с.
11. Крастин О.П. Разработка и интерпретация моделей корреляционных связей в экономике. - Рига: Зинатне, 2007. – 408 с.
12. Маркин Ю.П. Анализ внутрихозяйственных резервов. М: Финансы и статистика,2005. – 379 с.
13. Муравьев А.И. Теория экономического анализа: проблемы и решения. М: Финансы и статистика,2008. – 391 с.
14. Панков Д.А. Современные методы анализа финансового положения М.: ООО Профит.2005. – 233 с.
15. Плошка Б.Г. Группировка и система статистических показателей. М.: Статистка, 2005.- 176 с.
16. Рафиков М.М. Экономика, организация и планирование сельскохозяйственного производства. M: Экономика, 2008. – 411 с.
17. Савицкая Г.В. Теория анализа хозяйственной деятельности М: ИСЗ, 2005. -220 с.
18. Савицкая Г.В. Анализ хозяйственной деятельности промышленного предприятия. М.: ИСЗ, 2005. – 109 с.
19. Сергеев С.С. Сельскохозяйственная статистика с основами экономической статистики. М.: Финансы и статистика, 2005. – 89 с.
20. Статистическое моделирование и прогнозирование / Под ред. А.Г. Гранберга. М.: Финансы и статистика, 2006.- 383 с.
21. Стражев В.Н. Оперативное управление предприятием, проблемы учета и анализа Мн.: Наука и техника,2007. – 330 с.
22. Теория экономического анализа (под ред. Шеремета А.Д. М.: Прогресс. 2006. – 590 с.
23. Шеремет А.Д. Методика финансового анализа предприятияМ.: ИПО МП, 2006. – 450 с.
24. Экономика предприятия Под. ред.проф. В.Я. Горфинкеля, М.,2006. – 189 с.
Похожие работы
... принять от хозяйства сахарную свеклу, не соответствующую по качеству условиям договора, со скидкой 20% от зачетного веса. 4. Совершенствование организации производства и реализации сахарной свеклы и продукции ее переработки в СХПК «Куликовский» При совершенствование организации производства, как отрасли, так и отдельно взятой культуры, необходимо учитывать выполнение договорных обязательств ...
... 0,9 -0,3 Фондоемкость, руб. 0,8 1,0 1,1 +0,3 Производительность труда, тыс. руб. 303,0 310,0 359,7 +56,7 Уровень рентабельности, % +5,7 +7,8 +10 +4,3 3. Экономико-статистический анализ производства сахарной свеклы Экономико-статистический анализ заключается во всестороннем изучении состояния сельского хозяйства, с тем, чтобы сделать выводы о закономерностях его развития и ...
... продукция на душу населения была в 5 раз меньше, чем в развитых капиталистических странах(с10). Сравнительный анализ экономических курсов Ф. Рузвельта и И. Сталина Две великие державы, с противоположными взглядами на ведение политики, экономики и различным менталитетом, но одинаково жаждущих мировое господство, СССР и США, в начале 20 века ищут пути выхода из кризиса в экономике… Изучая ...
... , сокращения себестоимости и увеличения цены реализации составляет 3911,21 тыс. руб. Заключение Проведенные исследования позволили сделать следующие выводы. СХА имени Чапаева является средним по размеру хозяйством Староюрьевского района Тамбовской области. Оно расположено в северной природно-хозяйственной зоне области, в четырех километрах от железнодорожной станции и в 100 километрах от г. ...
0 комментариев