Теория статистики

Задача 1

Стаж работы и средняя оплата труда двадцати работников (по данным выборочного обследования):

Таблица 1 – Стаж работы и средняя оплата труда двадцати работников

№ п.п.	Стаж работы, лет	Оплата труда, тыс. усл. руб.	№ п.п.	Стаж работы, лет	Оплата труда, тыс. усл. руб.
1	2,0	19,3	11	3,0	20,9
2	5,5	24,7	12	7,5	28,0
3	6,0	25,0	13	7,0	24,8
4	8,0	27,2	14	11,0	32,2
5	2,5	21,4	15	14,5	34,8
6	4,5	24,1	16	13,0	32,0
7	10,0	31,5	17	5,0	25,5
8	9,0	30,3	18	16,0	36,4
9	1,5	18,1	19	3,7	22,3
10	12,0	29,8	20	15,0	35,5

С целью изучения зависимости между стажем работы и оплатой труда работников произведите группировку работников по стажу их работы, образовав 5 групп с равными интервалами.

По каждой группе и по всем группам вместе определите:

1.   Число работников.

2.   Общий стаж работы всех работников и средний в расчете на 1 работника.

3.   Сумма оплаты труда всех работников и среднюю оплату 1 работника.

Результаты группировки оформить в таблице. Указать вид таблицы и вид группировки. Сделайте выводы.

Решение:

Определим размер интервала  по формуле:

,

гдеX_max – максимальное значение признака;

X_min – минимальное значение признака;

n – заданное количество групп.

Определяем границы для каждой группы и производим группировку.

Таблица 2 – Границы групп

Группы	Границы групп
	Нижняя	Верхняя
I	1,5	4,4
II	4,4	7,3
III	7,3	9,2
IV	9,2	12,1
V	12,1	16,0

Таблица 3 – Группировка работников по стажу работы

Группы работников по стажу работы, лет	№ п. п.	Стаж работы, лет	Оплата труда, тыс. усл. руб.
1,5 – 4,4	9	1,5	18,1
	1	2,0	19,3
	5	2,5	21,4
	11	3,0	20,9
	19	3,7	22,3
Итого	5	12,7	102,0
4,4 – 7,3	6	4,5	24,1
	17	5,0	25,5
	2	5,5	24,7
	3	6,0	25,0
	13	7,0	24,8
Итого	5	28,0	124,1
7,3 – 9,2	12	7,5	28,0
	4	8,0	27,2
	8	9,0	30,3
Итого	3	24,5	85,5
9,2 – 12,1	7	10,0	31,5
	14	11,0	32,2
	10	12,0	29,8
Итого	3	33,0	93,5
12,1 – 16,0	16	13,0	32,0
	15	14,5	34,8
	20	15,0	35,5
	18	16,0	36,4
Итого	4	58,5	138,7
Всего	20	156,7	543,8

Таблица 4 – Зависимость между стажем работы работников и их оплатой труда

Группы работников по стажу работы, лет	Количество работников, чел.	Стаж работы, лет		Оплата труда, тыс. усл. руб.
		Общий	Средний на 1 работника	Всего	Средняя на 1 работника
1	2	3	4=3:2	5	6=5:2
1,5 – 4,4	5	12,7	2,5	102,0	20,4
4,4 – 7,3	5	28,0	5,6	124,1	24,8
7,3 – 9,2	3	24,5	8,2	85,5	28,5
9,2 – 12,1	3	33,0	11,0	93,5	31,2
12,1 – 16,0	4	58,5	14,6	138,7	34,7
Итого	20	156,7	7,8	543,8	27,9

Вывод: По вычисленным показателям, которые представлены в таблице 4 видно, что с увеличением среднего стажа работы на 1 работника увеличивается и средняя оплата труда на 1 работника. Хотя из таблицы 3 видно, что в IV группе есть работник, у которого оплата труда меньше, чем у работника III группы. Этот случай нельзя считать закономерностью.

 
Задача 2

Выпуск однородной продукции по подразделениям объединения за два периода:

Таблица 5 – Исходные данные выпуска однородной продукции

№ п.п.	Базовый период		Отчетный период
	Выпуск продукции, тыс. ед.	Себестоимость единицы, усл. руб.	Выпуск продукции, тыс. ед.	Общая себестоимость выпуска продукции, тыс. усл. руб.
1	280	10,1	290	2958
2	510	10,0	530	5353
3	350	10,2	340	3400
4	600	9,8	620	6014

1.               Исчислите среднюю себестоимость единицы продукции в целом по объединению за каждый период.

2.               Проанализируйте динамику средней себестоимости единицы продукции, исчислив абсолютное и относительное ее изменение.

3.               Сделайте выводы.

Решение:

Средняя арифметическая взвешенная себестоимости единицы продукции определяется по формуле:

,

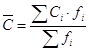где  – значение частоты повторения признака.

Таблица 6 – Данные для определения средней арифметической взвешенной себестоимости единицы продукции в базисном периоде

№ п.п.	1	2	3	4	Итого
Выпуск продукции, тыс. ед. ()	280	510	350	600	1740
Себестоимость единицы, усл. руб. ()	10,1	10,0	10,2	9,8	-
Расчетные данные
Общая себестоимость выпуска продукции, тыс. усл. руб. ()	2828	5100	3570	5880	17378

Средняя арифметическая взвешенная себестоимости единицы продукции в базисном периоде:

Определим среднюю гармоническую взвешенную себестоимости единицы продукции по формуле:

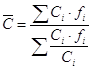
Средняя гармоническая взвешенная себестоимости единицы продукции в отчетном периоде:

Таблица 7 – Показатели анализа динамики себестоимости единицы продукции

№ п/п	Себестоимость единицы продукции в базисном периоде, усл. руб.	Себестоимость единицы продукции в отчетном периоде, усл. руб.	Абсолютные приросты, усл. руб.	Темпы прироста, %
1	10,1	10,1	-	100
2	10,0	10,0	-	100
3	10,2	10,2	-	100
4	9,8	9,7	-0,1	99

Вывод: Значения себестоимости единицы продукции в отчетном и базисном периоде имеют постоянные величины, т.е. не меняются. Только для изделия под № 4 себестоимость единицы продукции в отчетном периоде уменьшилась на 0,1 усл. руб. по сравнению с базисным.

  Задача 3

Распределение работников по затратам времени на производство изделия "А".

Таблица 8 – Исходные данные распределения работников по затратам времени на производство изделия "А"

Группы работников по затратам времени на изделие, мин.	До 5	5-7	7-9	9-11	11 и более
Количество работников	25	19	42	8	6

Определить:

1.         Средние затраты времени одним работником на производство единицы изделия.

2.         Модальный размер затрат времени одним работником на производство единицы изделия.

3.         Среднее квадратическое отклонение и коэффициент вариации.

По вычисленным значениям сделать выводы.

Решение:

Таблица 9 – Расчетные показатели

Группы работников по затратам времени на изделие,	Количество работников,	Средние затраты времени одним работником на производство единицы изделия,	Расчетные показатели
3-5	25	4	3	9	75	225
5-7	19	6	1	1	19	19
7-9	42	8	1	1	42	42
9-11	8	10	3	9	24	72
11-13	6	12	5	25	30	150
Итого	100	-	-	-	190	508

Средняя арифметическая взвешенная себестоимости единицы продукции определяется по формуле:

,

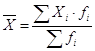где  – значение частоты повторения признака.

Модальный размер затрат времени одним работником на производство единицы изделия определяется по формуле:

,

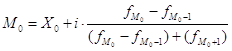где М₀ – статистическая мода;

Х₀ – нижняя граница (минимальное значение) модального интервала;

i – размер модального интервала (разность между верхней и нижней границей модального интервала);

– частота модального интервала;

– частота предмодального интервала;

– частота интервала после модального.

Среднее квадратическое отклонение определяется по формуле:

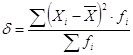
Коэффициент вариации определяется по формуле:

Вывод: Большинство работников тратят времени на производство единицы продукции 7,8 мин. Затраты времени одним работником на производство единицы изделия в среднем отклоняются от среднего значения на 5,08 мин.

В среднем затраты времени одним работником на производство единицы изделия отклоняется на 72,57%. Данная совокупность не однородная, так как коэффициент вариации больше 33%.

  Задача 4

Запасы сырья и материалов производственного предприятия на начало каждого года (тыс. усл. руб.).

Таблица 10 – Исходные данные запасов сырья и материалов производственного предприятия на начало каждого года (тыс. усл. руб.)

Годы	1	2	3	4	5
Запасы	520	536	550	572	594

С целью изучения динамики запасов сырья и материалов исчислить:

1.         Абсолютные приросты, темпы роста и прироста по годам (цепная система). Результаты расчетов представить в таблице.

2.         Среднегодовой размер запасов сырья и материалов.

3.         Средний абсолютный прирост, средний темп роста и прироста запасов из цепных показателей.

Укажите, к какому виду относится ряд динамики.

По исчисленным показателям сделать выводы.

Решение:

Таблица 11 – Показатели анализа динамики запасов сырья и материалов

Годы	Запасы, тыс. усл. руб.	Абсолютные приросты (цепные), тыс. усл. руб.	Темпы роста (цепные), %	Темпы прироста (цепные), %
1	520	-	-	-
2	536	16	103,1	3,1
3	550	14	102,6	2,6
4	572	22	104,0	4,0
5	594	22	103,8	3,8
Итого	2772	74	-	-

Среднегодовой размер запасов сырья и материалов определяется по формуле:

,

гдеЗ₁, З₂, З₃, З₄, З₅ – размер запасов сырья и материалов в первый, второй, третий, четвертый и пятый годы соответственно, тыс. усл. руб.;

n – количество лет.

Средний абсолютный прирост из цепных показателей запасов сырья и материалов определяется:

Средний темп роста из цепных показателей запасов сырья и материалов определяется:

Средний темп прироста запасов сырья и материалов из цепных показателей определяется:

Вывод: Среднегодовой размер запасов сырья и материалов составляет 554,4 тыс. усл. руб.

В среднем ежегодный прирост запасов сырья и материалов составил в размере 18,5 тыс. усл. руб. В среднем ежегодный темп роста запаса сырья и материалов составил 103,4%, а средний ежегодный прирост запаса сырья и материалов составил 3,4%.

  Задача 5

Данные о продаже товаров одной из коммерческих структур за два периода.

Таблица 12 – Данные о продаже товаров

Наименование товара	Общая стоимость проданных товаров (товарооборот), тыс. усл. руб.		Изменение цен на товары, %
	базисный период	отчетный период
А	228,4	320,8	+3,2
В	352,2	390,0	-0,1
С	460,4	510,2	+1,5

Вычислить общие индексы динамики:

1.         Общей стоимости проданных товаров (товарооборота).

2.         Индекс цен на товары, используя формулу среднего гармонического индекса.

3.         Индекс физического объема проданных товаров, используя взаимосвязь указанных индексов.

Произвести факторный анализ динамики товарооборота, определив абсолютное и относительное его изменение.

Сделать выводы по всем исчисленным показателям.

Решение:

Индекс общего товарооборота определяется:

,

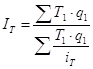гдеТ₁ – товарооборот отчетного периода, тыс. усл. руб.;

Т₀ – товарооборот базисного периода, тыс. усл. руб.;

 – индекс изменения цен на товары.

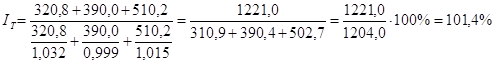
Индекс цен на товары, используя формулу среднего гармонического индекса определяется по формуле:

Средний товарооборот в базисном периоде определяется:

Индекс физического объема проданных товаров, используя взаимосвязь указанных индексов

,

Вывод: Товарооборот в отчетном периоде по сравнению с базисным увеличился на 17,3% или на 180 тыс. усл. руб., в том числе за счет изменения цен на товар - на 1,4%, что составило 17 тыс. усл. руб.

  Задача 6

С целью изучения тесноты связи между стажем работы (факторный признак, Х) и оплатой труда работников (результативный признак, У) исчислите корреляционное отношение по исходным данным и результатам группировки задачи № 1 данного варианта. Межгрупповая и общая дисперсии для расчета корреляционного отношения определяются по значениям результативного признака (оплата труда работников, У).

Поясните полученное значение корреляционного отношения.

Решение:

Таблица 13 – Зависимость между стажем работы работников и их оплатой труда

Исходная информация			Расчетные показатели
Группы работников по стажу работы, лет	Количество работников, чел.	Средняя оплата труда, тыс. усл. руб.	Оплата труда, тыс. усл. руб.	Отклонение вредней групповой от общей	Квадраты отклонений	Произведение квадрата отклонений на число работников
1,5 – 4,4	5	20,4	102,0	6,8	46,26	231,20
4,4 – 7,3	5	24,8	124,1	2,4	5,76	28,80
7,3 – 9,2	3	28,5	85,5	1,3	1,69	5,07
9,2 – 12,1	3	31,2	93,5	4,0	16,00	48,00
12,1 – 16,0	4	34,7	138,7	7,5	56,25	225,00
Итого	20	27,2	543,8	-	-	538,07

Средняя оплата труда для всех работников:

Межгрупповая дисперсия:

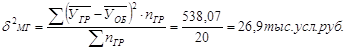
Таблица 14 – Показатели для определения общей дисперсии

Оплата труда, тыс. усл. руб.	19,3	24,7	25,0	27,2	21,4	24,1	31,5
	372,49	610,09	625,00	739,84	457,96	580,81	992,25
	7,9	2,5	2,2	0	5,8	3,1	4,3
	62,41	6,25	4,84	0	33,64	9,61	18,49
Итого	-	-	-	-	-	-	-

Оплата труда, тыс. усл. руб.	30,3	18,1	29,8	20,9	28,0	24,8	32,2
	918,09	327,61	888,04	436,81	784,00	615,04	1036,84
	3,1	9,1	2,6	6,3	0,8	2,4	5,0
	9,61	82,81	6,76	39,69	0,64	5,76	25,00
Итого	-	-	-	-	-	-	-

Оплата труда, тыс. усл. руб.	34,8	32,0	25,5	36,4	22,3	35,5	543,8
	1211,04	1024	650,25	1324,96	497,29	1260,25	15352,66
	7,6	4,8	1,7	9,2	4,9	8,3	-
	57,76	23,04	2,89	84,64	24,01	68,89	566,74
Итого	-	-	-	-	-	-	Итого

Общая дисперсия:

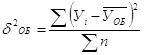
Общая дисперсия упрощенным способом:

Корреляционное отношение:

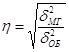
Вывод: Оплата труда работников зависит от стажа их работы на 97,43 %. Влияние других факторов составляет 2,57 %. Взаимосвязь между изучаемыми показателями высокая.

Список литературы

1.   Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник. – М.: Финансы и статистика, 1996 г.

2.   Ефимова М.Е., Петрова Е.В., Румянцев В.М. Общая теория статистики: Учебник. – М.: Финансы и статистика, 1996 г.

3.   Спирина А.А., Башина О.Э. Общая теория статистики. – М.: Финансы и статистика, 2001 г.

4.   Шмойлова Р.А. Теория статистики: Учебник. – М.: Финансы и статистика, 2001 г.

5.   Харченко Л.П., Долженкова В.Г., Ионин В.Г. Статистика: Учебное пособие. – М.: ИНФРА-М, 2003 г.