Теория статистики

Задача 1

Стоимость продукции и основных производственных фондов предприятия за отчетный период, тыс. усл. руб.

Таблица 1 – Исходные данные стоимости продукции и основных производственных фондов предприятия за отчетный период, тыс. усл. руб.

№ п.п.	Производство продукции	Основные фонды	№ п.п.	Производство продукции	Основные фонды
1	177,5	187,2	14	124,3	123,0
2	130,9	144,1	15	135,7	134,8
3	112,5	110,4	16	109,5	110,4
4	144,6	147,5	17	215,6	213,5
5	214,3	211,8	18	163,2	156,7
6	125,0	111,5	19	270,5	268,2
7	207,8	205,3	20	84,8	85,0
8	110,4	107,5	21	107,7	108,5
9	75,2	75,0	22	224,4	223,0
10	108,3	110,5	23	120,0	110,8
11	290,1	259,3	24	92,1	91,5
12	105,8	105,0	25	211,3	210,6
13	262,0	265,5	26	208,1	206,5

С целью установления зависимости между стоимостью основных фондов и выпуском продукции произведите группировку предприятий по стоимости основных фондов, образовав 4 групп с равными интервалами.

По каждой группе и по всем группам предприятий в целом посчитать:

1.   Число предприятий.

2.   Общую стоимость основных фондов и среднюю стоимость в расчете на одно предприятие.

3.   Общую стоимость производства продукции и ее среднюю стоимость в расчете на одно предприятие.

Результаты группировки оформить в таблице. Назвать вид таблицы и вид группировки.

Сделайте выводы.

Решение:

Определим размер интервала  по формуле:

,

гдеX_max – максимальное значение признака;

X_min – минимальное значение признака;

n – заданное количество групп.

Определяем границы для каждой группы и производим группировку.

Таблица 2 – Границы групп

Группы	Границы групп
	Нижняя	Верхняя
I	75,2	129,0
II	129,0	182,8
III	182,8	236,6
IV	236,6	290,4

Таблица 3 – Группировка по стоимости производства продукции

Группы по стоимости производства продукции, тыс. усл. руб.	№ п/п	Производство продукции, тыс. усл. руб.	Основные фонды, тыс. усл. руб.
75,2 – 129,0	9	75,2	75,0
	20	84,8	85,0
	24	92,1	91,5
	12	105,8	105,0
	21	107,7	108,5
	10	108,3	110,5
	16	109,5	110,4
	8	110,4	107,5
	3	112,5	110,4
	23	120,0	110,8
	14	124,3	123,0
	6	125,0	111,5
Итого	12	1272,9	1249,1
129,0 – 182,8	2	130,9	144,1
	15	135,7	134,8
	4	144,6	147,5
	18	163,2	156,7
	1	177,5	187,2
Итого	5	751,9	770,3
182,8 – 236,6	7	207,8	205,3
	26	208,1	206,5
	25	211,3	210,6
	5	214,3	211,8
	17	215,6	213,5
	22	224,4	223,0
Итого	6	1281,5	1270,7
236,6 – 290,4	13	262,0	265,5
	19	270,5	268,2
	11	290,1	259,3
Итого	3	822,6	793,0
Всего	26	4128,9	4083,1

Таблица 4 – Зависимость между стоимостью продукции и основными производственными фондами предприятий за отчетный период

Группы по стоимости продукции, тыс. усл. руб.	Число предприя-тий, шт.	Стоимость производства продукции, тыс. усл. руб.		Стоимость основных фондов, тыс. усл. руб.
		Общий	Средняя на 1 предприятие	Всего	Средняя на 1 предприятие
1	2	3	4=3:2	5	6=5:2
75,2 – 129,0	12	1272,9	106,1	1249,1	104,1
129,0 – 182,8	5	751,9	150,4	770,3	154,1
182,8 – 236,6	6	1281,5	213,6	1270,7	211,8
236,6 – 290,4	3	822,6	274,2	793,0	264,3
Итого	26	4128,9	158,8	4083,1	157,0

Вывод: По данным таблицы 4 видно, что с увеличением стоимости производства продукции, стоимость основных фондов уменьшается. Однако во второй группе с увеличением стоимости производства продукции, увеличивается и стоимость основных фондов.

  Задача 2

Данные о стоимости проданных товаров (товарооборот, тыс. усл. руб.) и численности работников торгового предприятия за два периода:

Таблица 5 – Исходные данные стоимости проданных товаров

№ п.п.	Базовый период		Отчетный период
	Товарооборот в расчете на 1 работника	Число работников, чел.	Товарооборот в расчете на 1 работника	Общий товарооборот за период
1	28,3	7	35,2	250,1
2	35,5	9	42,4	346,2
3	37,4	10	45,3	462,0
4	30,6	8	40,1	258,4
5	25,2	6	37,5	215,5

Исчислите средний размер товарооборота на одного работника по торговому предприятию в целом за каждый период и проанализируйте динамику, определив изменение показателя в денежном выражении и в процентах.

Дайте обоснование выбору формул для расчета средней величины в каждом периоде.

Сделайте выводы.

Решение:

Средний размер товарооборота на одного работника по торговому предприятию (средняя арифметическая взвешенная) определяется по формуле:

,

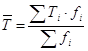где – товарооборот на одного работника по торговому предприятию, тыс. усл. руб.;

 – значение частоты повторения признака.

Таблица 6 – Данные для определения средней арифметической взвешенной себестоимости единицы продукции в базисном периоде

№ п.п.	1	2	3	4	5	Итого
Число работников, чел. ()	7	8	10	8	6	39
Товарооборот в расчете на 1 работника, тыс. усл. руб. ()	28,3	35,5	37,4	30,6	25,2	-
Расчетные данные
Общий товарооборот за период, тыс. усл. руб. ()	198,1	284,0	374,0	244,8	151,2	1252,1

Средняя арифметическая взвешенная товарооборота на одного работника по торговому предприятию в базисном периоде:

Определим среднюю гармоническую взвешенную товарооборота на одного работника по торговому предприятию по формуле:

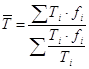
Средняя гармоническая взвешенная товарооборота на одного работника по торговому предприятию в отчетном периоде:

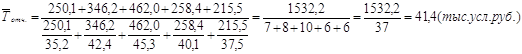
Таблица 7 – Показатели анализа динамики средней себестоимости единицы продукции

Секции	Товарооборот в расчете на 1 работника, тыс. усл. руб.	Товарооборот в расчете на 1 работника, тыс. усл. руб.	Абсолютные приросты, тыс. усл. руб.	Темпы прироста, %
1	28,3	35,2	+6,9	124,4
2	35,5	42,4	+6,9	119,4
3	37,4	45,3	+7,9	121,1
4	30,6	40,1	+9,5	131,1
5	25,2	37,5	+12,3	148,8

Вывод: Значения товарооборота в расчете на 1 работника в отчетном периоде по сравнению с базисным периодом увеличиваются. В денежном выражении максимальное увеличение товарооборота произошло для пятой секции. В процентном выражении наименьший темп прироста составляет 119,4% для второй секции.

Задача 3

Результаты выборочного обследования содержания влаги в продукции.

Таблица 8 – Исходные данные выборочного обследования содержания влаги в продукции

Влажность, %	До 10	10-14	14-18	выше 18
Число проб	15	40	35	10

Определить:

1.         Средний процент влажности всей партии обследованной продукции.

2.         Среднее квадратическое отклонение и коэффициент вариации.

3.         Модальное значение содержания влаги в продукции.

Сделать выводы по вычисленным показателям.

Решение:

Таблица 9 – Расчетные показатели

Влажность,	Количество проб,	Средний процент влажности всей партии обследованной продукции,	Расчетные показатели
6-10	15	8	6	36	90	540
10-14	40	12	2	4	80	160
14-18	35	16	2	4	70	140
18-22	10	20	6	36	60	360
Итого	100	-	-	-	300	1200

Средняя арифметическая взвешенная процента влажности всей партии обследованной продукции определяется по формуле:

,

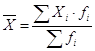где  – значение частоты повторения признака.

Модальный размер процента влажности всей партии обследованной продукции определяется по формуле:

,

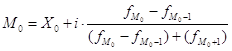где М₀ – статистическая мода; Х₀ – нижняя граница (минимальное значение) модального интервала; i – размер модального интервала (разность между верхней и нижней границей модального интервала); – частота модального интервала; – частота предмодального интервала; – частота интервала после модального.

Среднее квадратическое отклонение определяется по формуле:

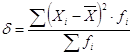
Коэффициент вариации определяется по формуле:

Вывод: Большинство проб имеет процент влажности обследованной продукции 13,3 %. Процент влажности всей партии обследованной продукции в среднем отклоняется от среднего значения на 12 %. В среднем процент влажности всей партии обследованной продукции отклоняется на 85,71%. Данная совокупность не однородная, так как коэффициент вариации больше 33%.

Задача 4

Сеть предприятий бытовых услуг населению административной единицы на начало каждого года.

Таблица 10 – Исходные данные сети предприятий бытовых услуг населению

Годы	1	2	3	4	5	6
Количество предприятий	260	275	282	290	302	315

Для изучения динамики количества предприятий исчислить:

1.         Абсолютные приросты, темпы роста и прироста предприятий по годам (цепная система). Результаты расчетов показателей оформите в таблице.

2.         Среднегодовое количество предприятий.

3.         Средний абсолютный прирост, среднегодовой темп роста и прироста.

По исчисленным показателям сделать выводы.

Таблица 11 – Показатели анализа динамики предприятий по годам

Годы	Количество предприятий, шт	Абсолютные приросты (цепные), шт.	Темпы роста (цепные), %	Темпы прироста (цепные), %
1	260	-	-	-
2	275	15	105,8	5,8
3	282	7	102,5	2,5
4	290	8	102,8	2,8
5	302	12	104,1	4,1
6	315	13	104,3	4,3
Итого	1724	55	-	-

Среднегодовое количество предприятий определяется по формуле:

,

гдеП₁, П₂, П₃, П₄, П₅, П₆ – количество предприятий в первый, второй, третий, четвертый, пятый и шестой годы соответственно, шт;

n – количество лет.

Средний абсолютный прирост из цепных показателей количества предприятий определяется:

Средний темп роста из цепных показателей количества предприятий определяется:

Средний темп прироста количества предприятий из цепных показателей определяется:

Вывод: Среднегодовое количество предприятий составляет 287 шт. В среднем ежегодный прирост количества предприятий составил в размере 11 шт. В среднем ежегодный темп роста количества предприятий составил 103,9 %, а средний ежегодный прирост количества предприятий составил 3,9 %.

Задача 5

Данные о реализации товара "А" на рынках города за два периода.

Таблица 12 – Данные о реализации товара "А"

№ п.п.	Базовый период		Отчетный период
	Цена за единицу, усл. руб.	Количество товара "А", тыс. ед.	Цена за единицу, усл. руб.	Общая стоимость продажи товара, тыс. усл. руб.
1	13	220	14	3500
2	15	260	15	4200
3	14	150	15	2850

Вычислить:

1.         Индекс динамики средней цены товара "А" по городу (переменного состава).

2.         Общий индекс цен товара "А" постоянного состава.

3.         Индекс структурных сдвигов в количестве продажи товара "А" по рынкам города, используя взаимосвязи указанных индексов.

Дайте экономическое обоснование исчисленным показателям.

Решение:

Индекс динамики средней цены товара "А" по городу (переменного состава) определяется:

,

где – средняя цена товара "А" в отчетном периоде, усл. руб.;

 – средняя цена товара "А" в базисном периоде, усл. руб.

Средняя цена товара "А" в базисном периоде определяется:

,

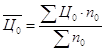гдеn₀ – количество товара "А", тыс.ед.

Средняя цена товара "А" в отчетном периоде определяется:

.

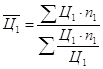Средняя цена товара "А" в отчетном периоде:

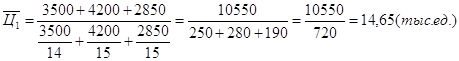
Индекс динамики средней цены товара "А" по городу (переменного состава):

Индекс цен товара "А" постоянного состава:

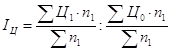
Индекс структурных сдвигов в количестве продажи товара "А" по рынкам города, используя взаимосвязи указанных индексов:

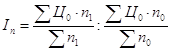
Вывод: Средняя цена за единицу товара "А" в отчетном периоде по сравнению с базисным увеличилась на 4,2%, в том числе за счет повышения цен на товар "А" - на 4,4%, за счет изменения количества товара средняя цена снизилась на 0,2%, что связано с увеличением доли продажи на рынке, где цена на товар была более дешевой.

Задача 6

Для изучения тесноты связи между стоимостью основных фондов (факторный признак, Х) и производством продукции (результативный признак, У) исчислите корреляционное отношение по исходным данным и результатам группировки задачи № 1.

Межгрупповую и общую дисперсию для расчета корреляционного отношения определить по значениям результативного признака.

Поясните полученное значение корреляционного отношения.

Решение:

Таблица 13 – Взаимосвязь между стоимостью основных фондов и производством продукции

Исходная информация			Расчетные показатели
Группы по производству продукции, тыс. усл. руб.	Количество предприятий, шт.	Средняя стоимость производства продукции на 1 предприятие, тыс. усл. руб.	Основные фонды, тыс. усл. руб.	Отклонение средней групповой от общей	Квадраты отклонений	Произведение квадрата отклонений на число предприятий
75,2 – 129,0	12	104,09	1249,1	52,95	2803,70	33644,43
129,0 – 182,8	5	154,06	770,3	2,98	8,88	44,40
182,8 – 236,6	6	211,78	1270,7	54,74	2996,47	17978,81
236,6 – 290,4	3	264,33	793,0	107,29	11511,14	34533,43
Итого	26	157,00	4083,1	-	-	86201,07

Средняя оплата труда для всех работников:

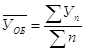
Межгрупповая дисперсия:

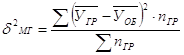
Таблица 14 – Расчеты для определения общей дисперсии

Основные фонды, тыс. усл. руб.	187,2	144,1	110,4	147,5	211,8	111,5
	35043,84	20764,81	12188,16	21756,25	44859,24	12432,25
	30,2	12,9	46,6	9,5	54,8	45,5
	912,04	166,41	2121,56	90,25	3003,04	2070,25
Итого	-	-	-	-	-	-

Основные фонды, тыс. усл. руб.	205,3	107,5	75,0	110,5	259,3	105,0
	42148,09	11556,25	5625,00	12210,25	67236,49	11025,00
	48,3	49,5	82,0	46,5	102,3	52,0
	2332,89	2450,25	6724,00	2162,25	10465,29	2704,00
Итого	-	-	-	-	-	-

Основные фонды, тыс. усл. руб.	265,5	123,0	134,8	110,4	213,5	156,7
	70490,25	15129,00	18171,04	12188,16	45582,25	24544,89
	108,5	34,0	22,2	46,6	56,5	0,3
	11772,25	1156,00	492,84	2171,56	3192,25	0,09
Итого	-	-	-	-	-	-

Основные фонды, тыс. усл. руб.	268,2	85,0	108,5	223,0	110,8	91,5
	71931,24	7225,00	11772,25	49729,00	12276,64	8372,25
	111,2	72,0	48,5	66,0	46,2	65,5
	12365,44	5184,0	2352,25	4356,0	2134,44	4290,25
Итого	-	-	-	-	-	-

Основные фонды, тыс. усл. руб.	210,6	206,5	4083,10
	44352,36	42642,25	731262,21
	53,6	49,5	-
	2872,96	2450,25	79442,81
Итого	-	-	Итого

Общая дисперсия:

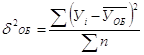
Общая дисперсия упрощенным способом:

Корреляционное отношение:

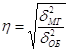
Вывод: Производство продукции зависит от стоимости основных фондов на 97,6 %. Влияние других факторов составляет 2,4 %. Взаимосвязь между изучаемыми показателями высокая.

Список литературы

1.   Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник. – М.: Финансы и статистика, 1996 г.

2.   Ефимова М.Е., Петрова Е.В., Румянцев В.М. Общая теория статистики: Учебник. – М.: Финансы и статистика, 1996 г.

3.   Спирина А.А., Башина О.Э. Общая теория статистики. – М.: Финансы и статистика, 2001 г.

4.   Шмойлова Р.А. Теория статистики: Учебник. – М.: Финансы и статистика, 2001 г.

5.   Харченко Л.П., Долженкова В.Г., Ионин В.Г. Статистика: Учебное пособие. – М.: ИНФРА-М, 2003 г.