Дисперсионный анализ

2          Дисперсионный анализ

Статистическое исследование вариации варианта ряда распределения связано, прежде всего, с практической необходимостью. В каждом конкретном случае их роль и значение определяются информацией на выходе, а также социально-экономическим значением исследуемого показателя. Что касается первого, то тут невозможно дать однозначный ответ. В частности, как быть в случае, когда в исследуемой совокупности значения отдельных вариантов существенно отличаются от всей совокупности и не являются типичными. Возьмём для примера ряд распределения, который характеризует годовой уровень доходов в пересчёте на одно домохозяйство. В таком ряду могут находиться домохозяйства с размером годового дохода, который не превышает 10000 грн., и такие размер доходов которых превышает миллион и более денежных единиц.

В экономической литературе по этому поводу не существует единой точки зрения. Одни учёные предлагают исключать нетиповые уровни исследуемого признака, другие эти действия считают незаконными по отношению к фактическим данным.

Наиболее приемлемым подходом является тот, при котором в каждом конкретном случае необходимо руководствоваться социально-экономическим значением исследуемого явления. Действительно, в случае, когда размер заработной платы работников бригады в месяц составил соответственно: 1200, 1700, 2200, 2700, 10000 условных единиц, то для статистической оценки объёмов месячного фонда заработной платы в целом нельзя исключать работника, который получил заработную плату 10000 условных единиц. Вместе с тем при подсчёте типовой для бригады средней заработной платы в месяц, заработную плату размером 10000 условных единиц необходимо исключить из исследуемого ряда распределения.

Вариация признака, в каждом конкретном случае, характеризуется позитивно или негативно, является желательной или нежелательной. Для практической и познавательной деятельности важным является познание роли и значения тех или иных факторов в формировании вариации признака. С этой целью используют дисперсионный анализ. В основе такого анализа лежит закон разложения общей дисперсии  на систематическую  (дельта) и случайную , или:

,

где  - общая дисперсия;  - межгрупповая дисперсия (систематическая, факторная);  - случайная дисперсия.

Общая вариация варьирует под влиянием систематических и случайных факторов.

Систематическая вариация или факторная является результатом действий постоянных, систематических факторов.

Случайная вариация – часть общей вариации, вызванная действием случайных факторов.

Дисперсионный метод анализа тесно связан с аналитическим группированием и построен с учётом теоретических и методологических условий проведения аналитического группирования. Прежде всего на основании логического экономического анализа определяют факторные и результативные признаки. Сравнивая групповые средние результативного признака с факторным, устанавливают наличие и размер связей, взаимозависимостей между причинами и следствиями.

Совместное использование дисперсионного и группировочного методов измерения взаимосвязей подразумевает расчёт межгрупповой (факторной) и внутригрупповой (случайной) дисперсии наряду с расчётом общей дисперсии. Межгрупповая вариация носит название систематической и характеризует влияние на результирующий признак систематических факторов, а её размер определяют с помощью формулы межгрупповой дисперсии:

,

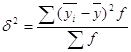где  - межгрупповая дисперсия;  - среднее значение групп;  - общая средняя;  - частота.

Учтём, что межгрупповая дисперсия характеризует отличия, вариацию групповых средних  около общей средней .

Случайная вариация, которая вызвана действием всех остальных факторов, за исключением фактора, который положен в основу группирования, оценивается с помощью внутригрупповой дисперсии. Она является средней величиной групповых дисперсий и расчитывается по формуле:

.

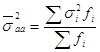Внутригрупповая дисперсия рассчитывается отдельно для каждой группы:

,

где  - значение признака отдельных элементов совокупности.

Для установления тесной связи между признаками межгрупповую дисперсию сравнивают с общей. Отношение межгрупповой дисперсии к общей называется корреляционным. Его обозначают греческой буквой  (эта) и рассчитывают по формуле:

.

Корреляционное отношение может изменяться от 0 до +/-1. В случае если =0 – межгрупповая дисперсия равняется нулю, а связь между факторным и результирующим признаками отсутствует.

Если =1, то межгрупповая дисперсия равна общей, а внутригрупповая равняется нулю. Связь функциональная. Чем ближе значение  к 1, тем теснее связь.

Рассмотрим пример расчёта дисперсий, используя данные из таблицы 3.

Таблица 3

Материалы для дисперсионного анализа

Сорт пшеницы	Количество участков ()	Урожайность на каждом участке ()
Мироновская 808	6	25; 27; 30; 35; 30;	177	29,5
Полесская	4	28; 24; 30; 30;	112	28,0
Киевская	10	40; 36; 35; 42; 45;	405	40,5
В целом	20	-	694	34,7

Вариация урожайности отдельно для каждого сорта пшеницы обозначается путём расчёта трёх внутригрупповых дисперсий. Для сорта Мироновская 808 она будет составлять:

.

Внутригрупповая дисперсия для сорта пшеницы «Полесская» будет составлять:

.

Соответственно для сорта «Киевская»:

.

Средняя из групповых дисперсий  равняется:

.

Рассчитаем межгруппоаую дисперсию:

где .

Используя взаимосвязь общей, межгрупповой и внутригрупповой дисперсии (правило сложения дисперсий), вычислим общую дисперсию .

Проверим наши расчёты, вычислив общую дисперсию по упрощённой формуле:

.

Правильность расчётов подтверждается.