Навигация
Математичні методи та моделі в управлінні аграрним виробництвом
РЕФЕРАТ НА ТЕМУ:
Математичні методи та моделі в управлінні аграрним виробництвом
Зміст
1. Склад машинних агрегатів та їх експлуатаційні показники
3. Прямі експлуатаційні витрати
4. Транспортне забезпечення механізованих технологічних процесів
5. Методика багатокритеріальної оцінки технологічних систем
6. Оптимізація використання комплексів машин
6. Аналіз показників машиновикористання та оцінка технічного оснащення виробництва
Використана література
1. Склад машинних агрегатів та їх експлуатаційні показники
Розрахунки по використанню машин у механізованих технологічних процесах включають обґрунтування та визначення робочих швидкостей руху, питомого та загального опору, коефіцієнту використання тягового зусилля, ефективної потужності двигуна та ступеню її використання, змінної продуктивності агрегату, витрати палива та мастильних матеріалів на одиницю роботи, витрати праці та коштів, необхідної кількості основних та допоміжних агрегатів і транспортних засобів.
Робоча швидкість агрегату
Робоча швидкість повинна бути в межах агротехнічнодопустимої (Табл.1), забезпечуватись потужністю двигуна енергетичного засобу та конкретною його передачею.
Таблиця 1.
Рекомендовані швидкості руху машинних агрегатів
| Основні операції | км/год |
| Оранка | 4…12 |
| Снігозатримання | 6…12 |
| Лущення дисковими знаряддями | 8…12 |
| Боронування зубовими боронами | 5…13 |
| Боронування голчастими боронами | 8…12 |
| Суцільна культивація | 6…12 |
| Коткування | 6…15 |
| Внесення мінеральних добрив | 8…20 |
| Внесення органічних добрив | 9…13 |
| Посів зернових | 7…14 |
| Посів кукурудзи, соняшника | 4…12 |
| Посів цукрового буряку | 5…8 |
| Посадка картоплі | 4…10 |
| Посадка розсади | 0,6…3,5 |
| Міжрядна культивація кукурудзи, соняшника | 6…12 |
| Обприскування | 6…10 |
| Підгортання картоплі | 5…7 |
| Збирання трав на сіно | 6…12 |
| Збирання трав на зелений корм | 6…8 |
| Скошування зернових у валки | 6…10 |
| Збирання зернових | 3…8 |
| Збирання кукурудзи: на зерно | 4…10 |
| на силос | 5…12 |
| Збирання картоплі: комбайнами | 1…5 |
| копачами | 2…8 |
| Збирання цукрового буряку | 3…9 |
У тому випадку, коли є можливість комплектувати агрегати різної ширини захвату, бажано вибирати передачу трактора, яка має тягове зусилля близьке до його тягового класу.
Для тягових агрегатів (оранка, культивація, посів безприводними сівалками та ін) в діапазоні агротехнічнодопустимих швидкостей руху вибирають передачі трактора, що знаходяться в цьому діапазоні, виходячи з умови:
Vmin £ VT £ Vmax;
Де VT - теоретична швидкість руху агрегату на даній передачі.
Робоча швидкість руху агрегату дорівнює:
Vp = VT hδ,
Де hδ - коефіцієнт, що враховує втрату швидкості від буксування.
Коефіцієнт, що враховує втрату швидкості від буксування дорівнює:
hδ = 1 - δ / 100;
Де δ - коефіцієнт буксування в%;
3% - гусеничні трактори;
12% - колісні 4К4;
16% - колісні 4К2.
На вибраних передачах визначають тягові зусилля трактора.
Для тягово-приводних агрегатів та самохідних машин визначають максимальну допустиму швидкість, яку забезпечує потужність двигуна.
Для тягово-приводного агрегату:
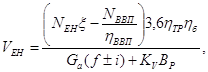 км/год.,
км/год.,
де
| NЕН | - | номінальна ефективна потужність двигуна трактора, кВт; |
| x | - | ступінь використання ефективної потужності двигуна (x = 0,9); |
| NВВП | - | потужність, що реалізується через ВВП, кВт; |
| hВВП | - | ККД механізму приводу ВВП (hВВП = 0,95); |
| hТР | - | ККД трансмісії приводу рушіїв трактора (hТР = 0,9); |
| і | - | величина підйому; |
| Ga | - | вага агрегату, що в загальному випадку включає вагу трактора, робочих машин, зчіпки, робочого матеріалу (насіння, добрива, зібраний урожай і т.д.), кН; |
| f | - | коефіцієнт опору кочення; |
| Кv | - | питомий опір при робочій швидкості агрегату, кН/м; |
| Вр | - | робоча ширина захвату, м. |
Самохідні збиральні машини по характеру витрат енергії умовно можна поділити на дві групи:
машини, витрата енергії якими істотно не залежить від урожайності (бурякозбиральні, картоплезбиральні та інші з підкопуючими робочими органами);
машини, витрата енергії якими залежить від урожайності (зернозбиральні, кукурудзозбиральні, кормозбиральні).
Для першої групи машин допустима швидкість визначається рівністю:
![]() км/год.,
км/год.,
де
| NP | - | потужність, необхідна на збирання з одного рядка, кВт; |
| nP | - | кількість рядків, шт; |
| hк | - | ККД трансмісії комбайна. |
Для другої групи машин:
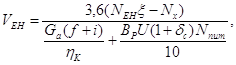 км/год
км/год
де
| Nx | - | потужність, що витрачається на холостий хід механізмів комбайна, кВт; |
| BP | - | робоча ширина захвату; м. |
| U | - | урожай зерна, т/га; |
| δс | - | соломистість (відношення маси соломи до маси зерна); |
| Nпит | - | питома потужність, яка необхідна для обмолоту (подрібнення) одиниці маси урожаю, кВт с/кг. |
Для тягово-приводного збирального агрегату:
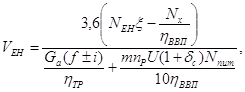 км/год
км/год
де
| Gа | - | вага агрегату, кН; |
| m | - | ширина міжрядь, м. |
Для машин з обмеженою пропускного здатністю (зернозбиральні комбайни) визначається швидкість, обумовлена пропускною здатністю:
![]() км/год.,
км/год.,
де
| qф | - | фактична для заданих умов пропускна здатність, кг/с. |
Питомий і загальний опір та коефіцієнт використання тягового зусилля
Ці показники визначають для тягових та тягово-приводних агрегатів. Питомий опір с. /г. машин при робочій швидкості дорівнює:
для плугів:
![]() кН/м2;
кН/м2;
для інших с. /г. машин:
![]() кН/м;
кН/м;
де
| КV | - | розрахунковий питомий тяговий опір сільськогосподарських машин з урахуванням швидкості руху, кН/м2 (кН/м); |
| КО | - | питомий тяговий опір машин при русі з швидкістю V0 =5 км/год, кН/м2; |
| DК | - | темп наростання питомого (тягового) опору машин при збільшенні швидкості руху агрегату на 1 км/год,%; |
Загальний питомий опір дорівнює:
для тягових агрегатів
причіпних плугів
Кзаг = Кv а + gм с і, кН/м;
начіпних плугів
Кзаг = Кv a + gм (l fТР + с і), кН/м,
інших причіпних с. /г. машин
Кзаг = Кv + gм і + gзч (fзч + і), кН/м;
інших начіпних с. /г. машин
Кзаг = Кv + gм (lfТР + і), кН/м;
для тяговопривідних агрегатів
причіпних
![]() кН/м;
кН/м;
Начіпних
![]() кН/м;
кН/м;
де
| а | - | глибина оранки, м; |
| gм | - | питома вага машини, кН/м; |
| c | - | коефіцієнт, що враховує наявність ґрунту на корпусах плуга (с = 1,1…1,4); |
| і | - | величина підйому; |
| l | - | коефіцієнт, що враховує довантаження трактора начіпною машиною; |
| fТР, fзч | - | коефіцієнт опору коченню трактора і зчіпки; |
| в | - | ширина захвату машини (корпуса плуга), м; |
| RВВП | - | додатковий опір, еквівалентний навантаженню, що передається через ВВП, кН. |
Додатковий опір дорівнює
![]() кН;
кН;
де
| NВВП | - | потужність, що реалізується через ВВП, кВт; |
| hТР | - | коефіцієнт корисної дії трансмісії (hТР = 0,95); |
| Vp | - | робоча швидкість руху агрегату, км/год. |
Максимально можлива ширина захвату агрегату рівна
![]() м;
м;
де
| Ргак | - | тягове зусилля на вибраній передачі, кН. |
Розрахункова кількість машин (корпусів плуга) в агрегаті рівна
![]()
де
| вк | - | конструктивна ширина захвату однієї машини (корпуса плуга), м. |
Фактичну кількість машин (корпусів плуга) приймають рівною цілому числу, виконуючи умову:
пф £ п р.
Якщо в агрегаті більше однієї машини, підбирають зчіпку, виконуючи умову
Фзч розр = (пф - 1) в £ Фзч, м;
де
| Фзч | - | фронт зчіпки, м. |
Загальний опір машин в агрегаті дорівнює
Ra = Kзаг вк пф, кН
Коефіцієнт використання тягового зусилля
![]()
де
| Ргак | - | тягове зусилля трактора на даній передачі. |
Необхідна ефективна потужність двигуна та ступінь її використання
Для тягових агрегатів:
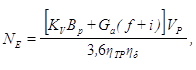 кВт
кВт
де
| Gа | - | вага агрегату, кН; |
| hТР | - | коефіцієнт корисної дії трансмісії трактора. |
hТР = haц · hbк,
де
| hц, hк | - | відповідно ККД циліндричних (0,98…0,99) і конічних (0,97…0,98) пар; |
| a, b | - | відповідно кількість циліндричних і конічних пар. |
Для тягово-приводних агрегатів:
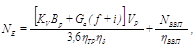 кВт
кВт
Для самохідних збиральних агрегатів витрати енергії якими мало залежать від урожайності:
![]() кВт
кВт
де
| hк | - | ККД трансмісії комбайна (0,80…0,85). |
Для самохідних збиральних агрегатів витрати енергії якими істотно залежать від урожаю:
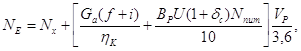 кВт
кВт
Для тягово-приводного збирального агрегату:
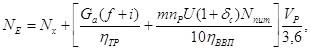 кВт
кВт
Ступінь використання ефективної потужності двигуна
![]() (11.1)
(11.1)
де
| NEH | - | номінальна ефективна потужність двигуна, кВт. |
Кінематичні характеристики агрегату та загінки і продуктивність агрегату. Для тягових агрегатів:
Робоча ширину захвату агрегату дорівнює:
Вр = вк·пф·b, м;
де
| b | - | коефіцієнт використання ширини захвату (табл.1.5). |
Робоча довжина загінки рівна
Lp = L - 2·E, м;
де
| L | - | довжина загінки, м; |
| Е | - | ширина поворотної смуги, м. |
Ширина поворотної смуги дорівнює: для петльових поворотів
Е = 3·Rп + е, м;
для безпетльових поворотів
Е = 1,5·Rп + е, м;
де
| Rn | - | радіус повороту агрегату, м; |
| е | - | довжина виїзду, м. |
Довжина виїзду агрегату рівна: для причіпних агрегатів -
е = (0,5…0,75) ·lК, м;
для начіпних агрегатів із задньою начіпкою –
е = 0,1·lК, м;
для начіпних агрегатів з передньою начіпкою -
е =·- lК, м;
де
| lК | - | кінематична довжина агрегату, м. |
Кінематична довжина агрегату рівна
lК = lТР + lзч + lм, м;
де
| lТР, lзч, lм | - | кінематична довжина відповідно трактора, зчіпки та сільськогосподарської машини, м. |
Після визначення розрахункового значення ширини поворотної смуги Е фактичне її значення приймається із умови
Еф = п Вр ³ Е, м;
де
| п | - | коефіцієнт кратності (п =1, 2, 3, …, і). |
Середня довжина повороту агрегату Lx, що приходиться на один робочий хід, та оптимальна ширина загінки C для різних способів руху агрегатів приведена в таблиці 2.
Таблиця 2.
Середня довжина повороту та оптимальна ширина загінки
| Спосіб руху | Довжина повороту | Оптимальна ширина загінки |
| Всклад, врозгін | 0,5С + 2,5R + 2е |
|
| Човниковий | 6R + 2е | |
| Перекриттям | 0,5С + 1,5R +2е | 10 R |
| Круговий | (1…2) R | L / 5…8 |
| Комбінований безпетльовий | 0,5С + 2R + 2е |
|
| Діагональний човниковий | 6R + 2е | (0,75...1,0) L |
| Діагональний перехресний | 4R + 2е | (0,75...1,0) L |
Продуктивність агрегату
Продуктивність агрегату за годину зміни дорівнює
Wг = 0,1·Вр·Vр·t, га/год;
| t | - | коефіцієнт використання часу зміни. |
Коефіцієнт використання часу зміни дорівнює
![]()
де
| TР | - | час чистої роботи; |
| Tзм | - | тривалість зміни. |
Час чистої роботи за зміну ![]() визначимо знайшовши час чистої роботи за один цикл. Кількість циклів за зміну дорівнює –
визначимо знайшовши час чистої роботи за один цикл. Кількість циклів за зміну дорівнює –
![]()
де
|
| - | сума позациклових простоїв агрегату за зміну, що включає: підготовчо-заключний час; час на виконання технічного і технологічного обслуговування агрегату; час переїздів до місця роботи; час на власні потреби; |
| tц | - | тривалість циклу, год.; |
Тривалість циклу дорівнює:
для агрегатів, що не мають технологічних місткостей
![]() год.;
год.;
де
| tp | - | час чистої роботи за один цикл, год.; |
| tx | - | час виконання повороту, год.; |
| Lp | - | робоча довжина загінки, км; |
| Vp | - | робоча швидкість агрегату, км/год.; |
| Lx | - | довжина повороту, км; |
| Vx | - | швидкість агрегату при виконанні повороту, км/год.; |
для агрегатів з технологічними місткостями, що завантажують (вивантажують) їх в загінці
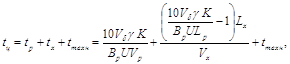 год.;
год.;
де
| tтехн | - | час завантаження (вивантаження) технологічної місткості, год.; |
| Vδ | - | об’єм технологічної місткості, м3; |
| γ | - | об’ємна вага с. /г. продукції, т/м3; |
| K | - | коефіцієнт заповнення або спорожнення; |
| Bp | - | робоча ширина захвату, м; |
| U | - | урожайність або норма висіву (внесення), т/га; |
для агрегатів з технологічними місткостями, що завантажують їх за межами загінки
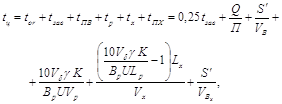
де
| tor | - | час очікування завантаження, год.; |
| tзав | - | час завантаження, год.; |
| tПВ | - | час руху з вантажем до загінки, год.; |
| tПХ | - | час руху до місця заправки, год.; |
| Q | - | маса вантажу, що перевозиться агрегатом, т; |
| П | - | продуктивність завантажувача, т/год.; |
| S’ | - | відстань від загінки до місця завантаження, км; |
| VB | - | транспортна швидкість руху з вантажем, км/год.; |
| VBx | - | транспортна швидкість руху без вантажу, км/год. |
Чистий час роботи за зміну (час виконання основної технологічної операції) дорівнює
Tр = tр·nц, год. (11.2)
Час поворотів за зміну рівний
Tх = tх·nц, год. (11.3)
Час завантаження (розвантаження) технологічних місткостей за зміну дорівнює
Tтехн = tтехн·nц, год.
Витрати палива і робочого часу на одиницю роботи та прямі експлуатаційні витрати
Витрату палива на одиницю роботи для агрегатів, що не мають технологічних місткостей та для агрегатів з технологічними місткостями, що завантажують (вивантажують) їх в загінці визначають за формулою:
![]() кг/га;
кг/га;
де
| QP, Qx, Qпм, Qз | - | годинна витрата палива, відповідно, при виконанні технологічного процесу, на поворотах, на переїздах до місця роботи, на зупинках з працюючим двигуном, кг; |
| ТР, Тx, Тпм, Тз | - | тривалість, відповідно, чистого часу зміни, поворотів, переїздів до місця роботи, зупинок з працюючим двигуном на протязі зміни, год.; |
| Wзм | - | виробіток за зміну, га. |
Тр, Тx визначають відповідно за формулами (11.2), (11.3). Тпм задається нормативно - 0,14 год.
Тз визначають за формулою:
Тз = Ттехн + (S Тнц - Тпм), год.
Витрату палива на одиницю роботи для агрегатів з технологічними місткостями, що завантажують їх за межами загінки визначають за формулою:
![]() кг/га;
кг/га;
де
| Qв | - | годинна витрата палива на переїздах із заповненою технологічною місткістю, кг; |
| Тв | - | тривалість переїздів з місця завантаження до загінки (із заповненою технологічною місткістю) протягом зміни, год. |
Час переїздів Тп включає в себе час переїздів до місця роботи Тпм та час переїзду до місця завантаження Тпx, тобто:
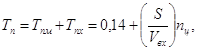
де
| Тпм | - | час переїздів до місця роботи (Тпм = 0,14 год); |
| Тпx | - | час переїздів до місця завантаження. |
Годинна витрата палива при різних режимах навантаження двигуна дорівнює:
Qг = NEH·gH·x, кг/год.;
де
| NЕН | - | номінальна ефективна потужність двигуна (Табл.3), кВт; |
| gН | - | питома витрата палива при номінальній потужності двигуна (Табл.3), кг/кВт год.; |
| x | - | ступінь використання ефективної потужності двигуна (визначається по рівнянню 11.1). |
Затрати робочого часу
![]() , люд. год. /га;
, люд. год. /га;
де
| пр | - | кількість робітників, які обслуговують агрегат; |
| Wг | - | продуктивність за годину змінного часу. |
Таблиця 3.
Експлуатаційні показники тракторів
| Назва параметрів | ЮМЗ-6Л | МТЗ-80, 82 | Т-70С | ДТ-75М | Т-150 | Т-150К | К-701 |
| Номінальна потужність, кВт | 44,1 | 58,8 | 51,5 | 66,2 | 110,3 | 121,3 | 220,6 |
| Номінальна частота обертання колінчастого валу, об/хв. | 1750 | 2200 | 2100 | 1750 | 2000 | 2100 | 1900 |
| Питома витрата палива, кг/кВт год. | 0,252 | 0,251 | 0,252 | 0,251 | 0,251 | 0,251 | 0,245 |
| Витрата палива на зупинках з працюючим двигуном, кг/год. | 1,2 | 1,4 | 1,2 | 1,9 | 2,2 | 2,4 | 4,0 |
| Експлуатаційна вага, кН | 31,1 | 33,47 35,71 | 44,15 | 66,5 | 74,0 | 79,0 | 131,0 |
| Кінематична довжина, м | 1,2/1,3 | 1,2/1,3 | 1,85 | 2,35/1,55 | 2,12-2,55 | 2,9-2,4 | 2,35-2.9 |
| Нормативне річне завантаження, год. | 1350 | 1350 | 1100 | 1300 | 1350 | 1350 | 1350 |
3. Прямі експлуатаційні витрати
Прямі експлуатаційні витрати на одиницю роботи дорівнюють:
С = С1 + С2 + С3 + С4, грн/га;
де
| С1 | - | оплата праці персоналу, що обслуговує агрегат, грн/га; |
| С2 | - | вартість витрачених паливо-мастильних матеріалів, грн/га; |
| С3 | - | відрахування на реновацію трактора і сільськогосподарських машин, що входять в агрегат, грн/га; |
| С4 | - | відрахування на капітальний і поточний ремонти, технічне обслуговування, грн/га. |
Оплата праці обслуговуючому персоналу дорівнює:
![]() грн/га;
грн/га;
де
| mi | - | кількість працівників на агрегаті і-ої кваліфікації; |
| ni | - | оплата праці за змінну норму виробітку робочого і-ої кваліфікації, грн; |
| WЗМ | - | змінна продуктивність агрегату, га. |
Вартість паливо-мастильних матеріалів дорівнює:
![]() грн/га;
грн/га;
де
| ЦK | - | комплексна ціна одного кілограма палива, грн/кг (орієнтовно - ЦK - 4,6 грн/кг); |
| QП | - | витрата паливо-мастильних матеріалів, кг/га. |
Витрата мастильних матеріалів визначається процентним відношенням до витрати палива:
дизельне (моторне) масло -4%;
трансмісійне масло -0,8%;
консистентні мастила -0,3%;
пусковий бензин -1,0%.
Відрахування на реновацію машин в агрегаті дорівнюють:
![]() грн/га;
грн/га;
де
| БТР, БМ | - | балансова вартість відповідно трактора і сільськогосподарської машини, грн.; |
| QТР, QМ | - | норми відрахувань на реновацію відповідно трактора і сільськогосподарської машини,%; |
| WЗ | - | продуктивність агрегату, га/год.; |
| tТР, tМ | - | зональне річне завантаження трактора і сільськогосподарської машини, год. |
Відрахування на капітальний, поточний ремонти і технічне обслуговування дорівнюють:
![]() грн/га;
грн/га;
де
| РТР, РМ | - | сумарна норма відрахувань на капітальний, поточний ремонт і технічне обслуговування відповідно трактора і сільськогосподарської машини,%. |
Визначення необхідної кількості агрегатів і транспортне забезпечення механізованих технологічних процесів
Необхідна кількість машинних агрегатів визначається за формулою:
![]()
де
| S | - | площа посіву, га; |
| Wг | - | продуктивність машинного агрегату за годину часу зміни, га/год.; |
| Тзм | - | тривалість зміни. Існуючі норми виробітку на механізовані сільськогосподарські роботи розраховані на нормативну 7‑годинну зміну, а для робіт, з шкідливими умовами праці (обпилювання, обприскування сільськогосподарських культур та ін) - на 6-годинну зміну. Таким чином Тзм дорівнює 7 або 6 год.; |
| Кзм | - | коефіцієнт змінності; |
| Д | - | агротехнічний строк, днів. |
Необхідна кількість транспортних засобів при застосуванні агрегатів з технологічними місткостями (бункерів) виходячи з умов потоковості збирання дорівнює:
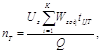
де
| Uз | - | урожайність с. /г. культури, т/га; |
| Wгод і | - | продуктивність і-го агрегату, га/год.; |
| tЦТ | - | тривалість циклу транспортного засобу, год.; |
| Q | - | фактична вантажопідйомність транспортного засобу, т. |
Тривалість циклу транспортного засобу дорівнює:
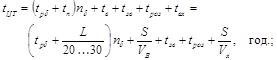
де
| tрδ | - | час розвантаження бункера (для зернозбирального комбайну tрδ =0,05 год); |
| L | - | довжина гонів, км; |
| S | - | відстань перевезення с. /г. продукції, км; |
| nδ | - | кількість бункерів, що завантажує транспортний засіб; |
| VB | - | швидкість руху транспортного засобу з вантажем, км/год (для автомобілів VB = 30 км/год); |
| tзв | - | тривалість зважування (tзв = 0,03 год); |
| tроз | - | тривалість розвантаження, год. (ЗИЛ-ММЗ-554М - tроз = 0,02 год.; КАМАЗ-5320 - tроз = 0,03 год); |
| Vх | - | швидкість руху транспортного засобу без вантажу, км/год. (для автомобілів Vх = 40 км/год). |
Необхідна кількість транспортних засобів при застосуванні агрегатів без технологічних місткостей (бункерів) виходячи з умов потоковості дорівнює
![]()
де
| tЦТ | - | тривалість циклу транспортного засобу, год.; |
| tр | - | час заповнення транспортного засобу, год. |
Тривалість циклу транспортного засобу дорівнює
![]() год.;
год.;
де
| tр | - | тривалість заповнення транспортного засобу, год.; |
| tв | - | тривалість руху з вантажем, год; |
| tрозв | - | тривалість розвантаження транспортного засобу, год; |
| tвх | - | тривалість руху без вантажу, год; |
| tзам | - | тривалість заміни транспортного засобу (tзам = 0,01 год); |
| Vδ | - | об’єм кузова транспортного засобу, м3; |
| γ | - | об’ємна вага с. /г. продукції, т/м3; |
| K | - | коефіцієнт заповнення кузова; |
| Bp | - | робоча ширина захвату агрегату, м; |
| U | - | урожайність с. /г. культури, т/га; |
| Vp | - | робоча швидкість агрегату, км/год.; |
| S | - | відстань перевезень с. /г. продукції, км; |
| VB | - | швидкість руху транспортного засобу з вантажем, км/год.; |
| Vx | - | швидкість руху транспортного засобу без вантажу, км/год. |
Математична модель (ММ) багатокритеріальної задачі
Системний підхід до обґрунтування рішень часто викликає необхідність застосовувати для оцінки альтернативних варіантів декілька критеріїв. У багатьох випадках рішення повинно відповідати декільком критеріям, що суперечать один одному (продуктивність - якість, рівень механізації - затрати паливо-мастильних матеріалів, втрати урожаю - затрати на виконання робіт), тобто зміна характеристик системи з метою покращення одного з них викликає погіршення іншого. Побудова єдиної шкали для оцінки всієї сукупності критеріїв, що мають різний фізичний зміст, викликає значні труднощі.
У загальному вигляді математична модель (ММ) багатокритеріальної задачі описується виразом:
MM = T, S,U, L, H, Y;
де
| T | - | тип багатокритеріальної задачі (оптимізація, ранжування, вибір); |
| S | - | множина варіантів характеристик системи, що оцінюється; |
| U | - | множина критеріїв, за якими оцінюється система; |
| L | - | шкала оцінок по кожному критерію; |
| H | - | система пріоритетів особи, що приймає рішення на множині варіантів S; |
| Y | - | правило вирішення, яке на множині варіантів S задає відношення переваги відповідно до системи пріоритетів H. |
Для пошуку кращого рішення необхідно множину варіантів S представити у просторі критеріїв U зі шкалами оцінок L і відповідно до правила вирішення Y впорядкувати цю множину, використовуючи систему пріоритетів Н.
У інженерній діяльності застосовують методи багатокритеріального вибору рішення із множини можливих варіантів.
Одним із методів багатокритеріального вибору є метод відстані до цілі. Суть його полягає в порівнянні J-го варіанту вихідної множини альтернативних варіантів з ідеалізованим варіантом.
За ідеалізований варіант приймають умовний варіант, якому приписуються кращі значення критеріїв з вихідної множини альтернативних варіантів. При цьому необхідно зауважити, що формування множини прийнятих критеріїв необхідно здійснювати при однаковому напрямку покращення всіх критеріїв. Пояснимо це на прикладі (табл.4).
Таблиця 4.
Вихідна множина альтернативних варіантів та критеріїв
| Склад машинних агрегатів | W, га/год. | G, кг/гa | Fg, га/кг | С, грн. /га | Fс, га/грн. | m |
| К-701+ЛДГ-20 | 8,3 | 4,5 | 0,22 | 314,5 | 0,00318 | - 0, 197 |
| Т-150К+ЛДГ-15 | 7,5 | 3,1 | 0,32 | 232,9 | 0,00429 | - 0,040 |
| Т-150К+ЛДГ-10 | 5,2 | 3,1 | 0,32 | 227,5 | 0,00439 | - 0,123 |
| Ідеалізований варіант | 8,3 | 0,32 | 0,00439 | 0 |
У нашому прикладі умова покращення всіх критеріїв в одному напрямку не дотримується, бо покращення продуктивності W спрямоване у бік її зростання, а витрата палива G та прямі експлуатаційні затрати С - у бік зниження.
Для забезпечення умови введемо критерії Fg = 1/G та Fс = 1/С, тобто обернені відповідно до витрати палива та прямих експлуатаційних затрат. Такі критерії характеризують розмір площі, що обробляється при затраті одиниці палива та одиниці коштів, а їх покращення, як і продуктивність, спрямовані у бік зростання.
У випадку, коли всі критерії мають однакову значущість, для кожного j‑го варіанту вихідної множини альтернатив визначається показник відстані до цілі за формулою:
![]()
де
| mі | - | відстань до цілі j - го варіанту; |
| N | - | число критеріїв; |
| Uij | - | значення i-го критерію j-го варіанту; |
| Uio | - | значення i-го критерію ідеалізованого варіанту. |
З вихідної множини альтернатив вибирається варіант, що знаходиться найближче до ідеалізованого варіанту, для якого m = 0.
У випадку коли критерії нерівноцінні, то визначають значущість критеріїв, використовуючи метод розставлення пріоритетів. Коефіцієнт значущості критеріїв розраховують при забезпеченні умови еi =1, наступним чином.
При попарному порівнянні критеріїв у відповідних комірках матриці (таблиця 5) проставляють коефіцієнти переваг. Якщо критерій в i-й стрічці має перевагу над критерієм в j-у стовпчику, то коефіцієнт приймають рівним - 1,5; при їх однаковій значущості - 1,0, а при меншій - 0,5.
Таблиця 5.
Матриця визначення значущості критеріїв
| Індекс критерію | К1 | К2 | К3 | S Кi | Pij | i |
| К1 | 1,0 | 1,0 | 0,5 | 2,5 | 7,0 | 0,27 |
| К2 | 1,0 | 1,0 | 0,5 | 2,5 | 7,0 | 0,27 |
| К3 | 1,5 | 1,5 | 1,0 | 4,0 | 11,5 | 0,46 |
|
| S Pij = 25,5 |
Коефіцієнти значущості lі визначають за формулою:
![]()
де
| Ріj | - | визначається, як сума добутків кожного елементу i-ї стрічки на елементи вектор-стовпчика S Kij; |
тобто,
![]()
Пояснимо це на прикладі (табл.12.2), у якому критерій К1 та критерій К2 рівнозначні, а критерій К3 домінує над критеріями К1 та К2, тобто
К1 = К2 í К3.
Тоді, для 1-ї стрічки матриці:
P1J = K11еK1+K12еK2+K13еK3 =1,0´2,5 + 1,0´2,5 + 0,5´4,0 =7,0.
Для 2-ї стрічки матриці:
Р2J = K21еK1 + K22еK2 + K23еK3 = 1,0´2,5 + 1,0´2,5 + 0,5 ´4,0 = 7,0.
Для 3-ї стрічки матриці:
Р3J = K31еK1 + K32еK2 + K33еK3 = 1,5´2,5 + 1,5´2,5 + 1,0´4,0 = 11,5.
Тоді коефіцієнти значущості критеріїв будуть рівні:
1 = 7,0/25,5 = 0,27;
2 =7,0/25,5 = 0,27;
3 = 11,5/25,5 = 0,46.
Визначивши коефіцієнти значущості критеріїв, розраховують відстань до цілі для заданої множини альтернативних варіантів:
![]()
де
| Uij | - | значення i-го критерію j-го варіанту; |
| Uio | - | значення i-го критерію ідеалізованого варіанту; |
| li | - | коефіцієнт значущості i-го критерію. |
З вихідної множини альтернатив вибирається варіант, що знаходиться найближче до ідеалізованого варіанту, для якого = 0.
Методика багатокритеріальної оцінки машинних агрегатів на персональному комп’ютері.
Комп’ютерна програма "Комплексна (багатокритеріальна) оцінка технічних та технологічних систем" дозволяє оцінити машинні агрегати одночасно по всім групам критеріїв (функціональним, експлуатаційних затрат, економічної ефективності, екологічності), тобто прийняти рішення щодо оптимальної структури комплексу машин, враховуючи всі фактори стосовно виробничих умов.
Комп’ютерна програма "Комплексна (багатокритеріальна) оцінка технічних та технологічних систем" дозволяє давати оцінку одночасно 100000 машинним агрегатам по 1500 критеріям.
Для початку роботи з програмою необхідно натиснути кнопку (Рис.1)"Розпочати роботу".

Рис.1. - Загальний вигляд вікна комп’ютерної програми "Комплексна (багатокритеріальна) оцінка технічних та технологічних систем"
Після появи вікна "Кількісні параметри задачі" (Рис.2) ввести кількість аналізуємих МА та кількість критеріїв і натиснути кнопку "Продовжити роботу".
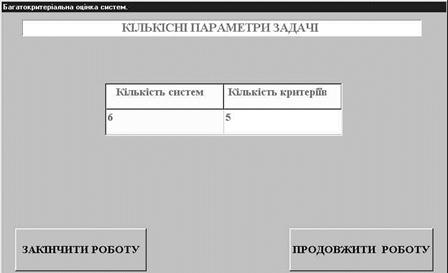
Рис.2. - Загальний вигляд вікна “Кількісні параметри задачі"
Після появи вікна "Вихідні дані для вибору систем" (Рис.3) ввести дані щодо складу МА та значення прийнятих критеріїв, після чого ввести, в залежності від напрямку покращення критеріїв ідеалізований варіант МА.
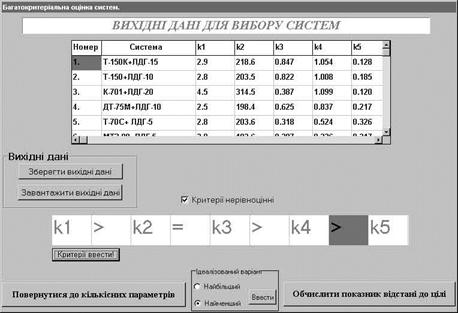
Рис.3. - Загальний вигляд вікна "Вихідні дані для вибору систем"
Далі вводиться порядок домінування критеріїв і натиснувши кнопки "Критерії ввести" та "Обчислити показник відстані до цілі" відкриваємо вікно "Ранжування систем" (Рис.4), де подається відстань до цілі та ранжування машинних агрегатів у залежності від прийнятих критеріїв та порядку іх домінування.
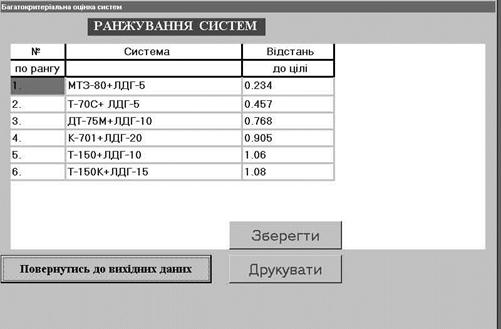
Рис.4. - Загальний вигляд вікна "Ранжування систем"
Для збереження одержаної інформації в персональному комп’ютері натиснути кнопку "Зберегти", для виводу інформації на принтер натиснути кнопку "Друкувати".
6. Оптимізація використання комплексів машин
Загальні положення про лінійні оптимізаційні моделі
У практиці обґрунтування інженерних рішень важливе місце займають оптимізаційні задачі з використанням детермінованих моделей.
Кожна технічна система функціонує для досягнення певної мети, а ступінь її досягнення і вся сукупність операцій, що відбувається в системі мають кількісну міру, тобто можуть бути описані математично.
Структура оптимізаційної моделі в загальному випадку включає цільову функцію F (x), яку необхідно мінімалізувати або максималізувати, обмеження hk (х) у вигляді рівнянь, обмеження gj (x) у вигляді нерівностей, а також область S допустимих значень незалежних змінних хі. Наприклад, якщо оптимізація передбачає мінімізацію цільової функції F (x), то математичну модель в загальному вигляді можна записати так:
F (x) = f (x1, x2,..., xn) ® min; (1.1)
hk (x) = 0,k = 1, 2,..., k; (1.2)
gj (x) ³ 0,g = 1, 2,..., j; (1.3)
xiH £ xi £ xib, i = 1, 2,..., N;
де xiH, xib - відповідно нижнє і верхнє значення і-ої змінної.
Оптимізаційні моделі можна класифікувати відповідно до вигляду функцій (1.1 - 1.3) та розмірності вектора х, тобто числом N змінних.
Задачу умовної оптимізації, в яких функції hk (x) і gj (x) є лінійними, входять у клас задач з лінійними обмеженнями. Якщо і цільова функція в них лінійна, то такі задачі відносяться до лінійного програмування.
Стандартна форма задач лінійного програмування
Серед методів багатомірної оптимізації з обмеженнями особливе місце займає лінійне програмування. Це пояснюється широким колом задач, що можуть бути зведені до лінійних моделей, а також розвинутим математичним і програмним забезпеченням методу лінійного програмування.
Задача лінійного програмування у стандартній формі має вигляд:
Z = C1x1 + C2x2 + … + Cnxn ® min
приa11x1 + a12x2 + … + a1nxn = b1 (1.4)
am1х1 + am2x2 + … + amnxn = bm
x1 ³ 0,x2 ³ 0,…xn ³ 0 (1.5)
b1 ³ 0,b2 ³ 0,…bm ³ 0
де
| n | - | число незалежних змінних; |
| m | - | число обмежень; |
| ai, Ci | - | числові коефіцієнти при змінних хі. |
Застосування загальних методів розв’язання задач лінійного програмування потребує зведення математичних моделей до певного однотипного вигляду.
Обмеження (1.4 - 1.5) можуть бути задані у вигляді нерівностей та рівнянь.
При цьому в нерівностях ліва і права частини можуть бути зв’язані знаками £ і ³.
Змінні, що входять у математичну модель, можуть бути додатними або не мати обмежень у знаку. Це народжує певну різноманітність математичних моделей, які можуть бути зведені до стандартної форми лінійних моделей, яка передбачає, що всі обмеження записуються у формі рівнянь з додатною правою частиною, значення всіх змінних моделі є додатними; цільову функцію потрібно мінімізувати або максимізувати.
Будь-яку лінійну модель можна звести до стандартної форми, використовуючи наступні прийоми.
Зведення нерівності до рівняння здійснюється шляхом введенням додаткової змінної, абсолютне значення якої дорівнює різниці між правою і лівою частинами. Ця змінна додається до лівої частини якщо має місце нерівність типу £.
Якщо вихідне обмеження є нерівністю типу ³, то додаткова змінна віднімається від лівої частини.
Значення правої частини рівняння повинно бути додатнім (не від’ємним). Якщо ця вимога не задовольняється, то ліву і праву частини рівняння множать на - 1.
Методика оптимізації використання комплексів машин методом лінійного програмування
Більшість технологічних операцій рільництва може бути виконана з використанням агрегатів на базі різних тракторів. Отже різні агрегати на виконанні однакових робіт мають різні техніко-експлуатаційні показники, що можуть істотно відрізнятися.
Тобто при обґрунтуванні складу комплексів машин є можливість вибирати різні варіанти використання сільськогосподарської техніки при виконанні однієї і тієї ж технологічної операції.
Оптимальним буде той варіант, який забезпечить мінімальні затрати ресурсів на виконання заданого обсягу робіт.
У загальному вигляді задачу оптимального використання комплексів машин можна сформулювати наступним чином:
у заданий календарний період (D днів) необхідно виконати певне число (m) технологічних, навантажувальних або транспортних операцій обсягом Fi (i=1, 2, …, m) (табл.4).
Для цього використовують n видів агрегатів j-го складу.
Годинна продуктивність j-го машинного агрегату (j=1, 2, …, n) становить Wij.
Прямі експлуатаційні витрати на виконання i-тої операції j-м машинним агрегатом складають Cij, витрати палива на одиницю роботи на виконання i‑тої технологічної операції j-м агрегатом складають Gij.
Кількість агрегатів кожного складу дорівнює naj.
Тривалість зміни у період, що планується, становить - Тзм.
Коефіцієнт змінності при виконанні операцій становить kзм.
Таблиця 4
Вихідні дані задачі
| Механізована робота | Обсяг робіт, F, га. | Машинний агрегат | ||||
| Продуктивність, Wij, га/год. / Прямі експлуатаційні затрати, Сij, грн/га. / Витрати палива, Gij, кг/га | ||||||
| 1 | 2 | 3 | … | n | ||
| Навантаження МД | F1 | W11/C11/G11 | W12/C12 /G12 | W13/C13/G13 | …/…/… | W1n/C1n /G1n |
| Транспортування МД | F2 | W21/C21/G21 | W22/C22 /G22 | W23/C23/G23 | …/…/… | W2n/C2n /G2n |
| Внесення МД | F3 | W31/C31/G31 | W32/C32 /G32 | W33/C33/G33 | …/…/… | W3n/C3n /G3n |
| Оранка | F4 | W41/C41/G41 | W42/C42 /G42 | W43/C43/G43 | …/…/… | W4n/C4n /G4n |
| … | … | … | … | … | …/…/… | … |
| і-та операція | Fm | Wm1/Cm1/Gm1 | Wm2/Cm2 /Gm2 | Wm3/Cm3/Gm3 | … / …/… | Wmn/Cmn /Gmn |
Необхідно знайти оптимальний план розподілу обсягу робіт за окремими агрегатами, який забезпечив би мінімальні затрати ресурсів (затрат праці Hij, витрати палива Gij, прямих експлуатаційних затрат Cij) на виконання всього обсягу робіт.
Побудову математичної моделі проводимо виходячи з того, що змінною величиною буде обсяг робіт Хij, що виконується всіма агрегатами j-го складу на і-тій операції за період D днів, а через Z - суму затрат ресурсів (затрат праці, витрати палива, прямих експлуатаційних затрат) на виконання всього обсягу робіт.
Цільову функцію виразимо залежністю:
при мінімізації затрат праці
![]()
при мінімізації витрати палива
![]()
при мінімізації прямих експлуатаційних затрат
![]()
Згідно з умовою задачі потрібно визначити такі значення Хij, щоб величина Z була мінімальною.
Можливі значення Хij будуть мати цілий ряд обмежень.
Зокрема Хij буде обмежене, в першу чергу, областю додатніх чисел, тобто
![]()
Друге обмеження стосується виконання повного обсягу робіт щодо кожної технологічної, навантажувальної або транспортної операції. Оскільки при виконанні і-тої операції можуть бути задіяні декілька складів агрегатів, то їх загальний виробіток Fi повинен дорівнювати:
![]()
Виробіток технологічних агрегатів дорівнює
Xij = xij, га.
Виробіток навантажувальних агрегатів дорівнює
Xij = H·xij, т.
Виробіток транспортних агрегатів дорівнює
Xij = H·S·xij, т·км.
Трете обмеження стосується не перевищення тракторами j-го складу наявного фонду часу Фj в заданому періоді, тобто загальний час використання тракторів j-го виду за D днів неповинен перевищувати фонду їх робочого часу Фj:
Тj ≤ Фj.
Час роботи агрегатів j-го типу на і-тій операції складає:
![]()
Так як трактори j-го типу можуть використовуватись при виконанні декількох операцій, то загальні затрати часу агрегатами цього типу в період D, будуть дорівнювати:
![]()
Фонд робочого часу Фj тракторів j-го виду за D днів становить
Фj = D·kзм·kп·Тзм·пj;
де
| kn | - | коефіцієнт, що враховує частку сприятливих для виконання операції днів. |
Тоді третє обмеження можна записати у вигляді
![]()
Математичне формулювання задачі набуде вигляду:
знайти оптимум цільової функції
Z (x) =f (H,G, C) → opt
при наступних обмеженнях:
I. ![]()
II. ![]()
III. ![]()
Запишемо в розгорненому вигляді математичну модель задачі.
Цільова функція, як загальна величина затрат ресурсів для виконання всього обсягу робіт (по всіх) виконаних комплексом машин, буде дорівнювати:
при оптимізації затрат праці
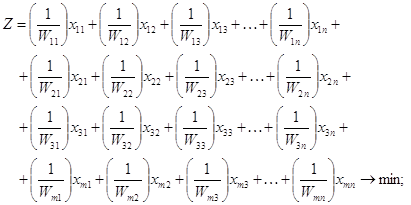
при оптимізації витрати палива
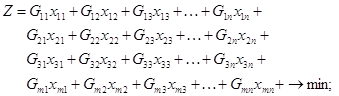
при оптимізації прямих експлуатаційних затрат
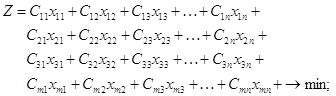
при умовах:
![]()
![]()
![]()
![]()
…
![]()
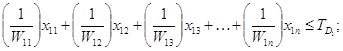
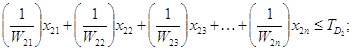
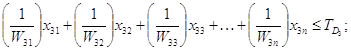
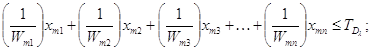
де![]()
Рішення даної задачі математичного програмування дозволяє оптимізувати використання комплексів машин.
Методика рішення задачі лінійного програмування графічним методом (для двохмірної оптимізації)
Рішення задачі лінійного програмування графічним методом (для двохмірної оптимізації) здійснюється наступним чином:
Визначають область допустимих рішень. Для цього в усіх обмеженнях почергово прирівнюють до нуля змінні X1 та X2 і знаходять відповідне значення іншої змінної. Ці значення будуть відповідати точкам перетину граничної прямої обмежень з осями координат X1 та X2.
Визначають напрям поширення області допустимих рішень відносно граничних прямих. Це встановлюють підставляючи в нерівності довільні значення X1 та X2. Якщо при цих значеннях умова обмеження задовольняється, то точка з координатами (X1і; X2і) знаходиться у півплощині допустимих рішень. Зручно задавати X1і = X2і = 0 і за умовою обмеження встановлювати приналежність початку координат до області допустимих рішень. Напрямок поширення півплощини допустимих рішень позначають штрихуванням. Область допустимих рішень знаходиться за сукупністю всіх обмежень. Якщо будь-яке з обмежень не впливає на область допустимих рішень, то воно є зайвим.
Положення прямої цільової функції Z знаходять довільним наданням її значення, при якому пряма перетинає в межах рисунка осі координат, відсікаючи на них відрізки Z/C1 і Z/C2. Проводячи плоскопаралельне переміщення прямої цільової функції в напрямку області допустимих рішень, знаходять точку або лінію на її межі, що відповідає оптимальному рішенню. При знаходженні максимуму цільової функції ця точка (лінія) буде знаходитись на верхній межі області допустимих рішень, а при пошуку мінімуму - на нижній.
Розв’язавши рівняння цільової функції з даними оптимальними значеннями X1 та X2 знаходять оптимальне значення цільової функції Z.
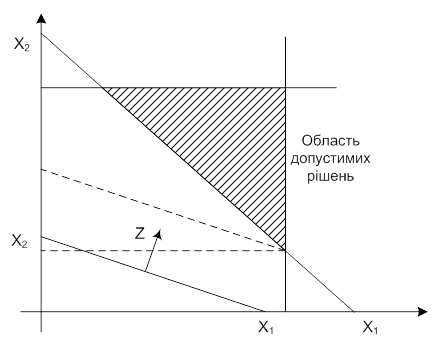
Рис.5. - Рішення задачі лінійного програмування графічним методом
Приклад побудови математичної моделі задачі оптимального використання комплексів машин з метою мінімізації прямих експлуатаційних затрат на виконання всього обсягу робіт методом лінійного програмування
Умови задачі:
У господарстві за 5 днів планується провести культивацію на площі 500 га.
На виконання цієї роботи може бути виділено:
Похожие работы
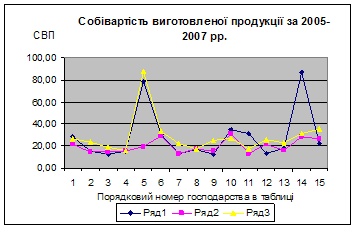
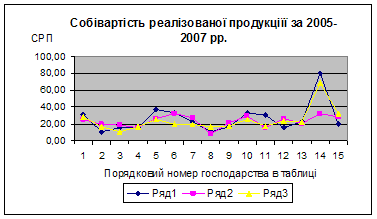
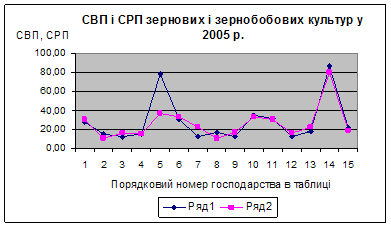
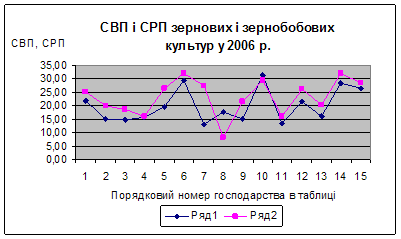
... змін, спостерігається тільки нестабільність та по деяких господарствах різкі зміни собівартості продукції, що виготовляється та реалізується. 3. Економіко-математичне моделювання в управлінні підприємством 3.1 Економіко-математичне моделювання урожайності сільськогосподарської продукції методом Брандона. Нехай економіко-математична модель матиме вид: , Де =; =; = ; Y - ...
... і і автоматичні. В управлінні економічними об’єктами більше використовуються різнорівневі автоматизовані системи державної статистики, фінансів, стандартів. Такі системи ще називають системами організаційного управління в якому використовуються також різновиди автоматизованих систем: інформаційно-пошукові, системи підтримки прийнятих рішень, інтелектуальні системи. Всі вони функціонують переважно ...
... коштів є важливим чинником у зниженні собівартості продукції чи виконаної роботи. Раціональне використання оборотних коштів залежить від правильного їхнього формування і ефективної організації виробництва. Зосередження н підприємствах зайвих оборотних коштів приводить до їхнього заморожування. Це завдає шкоди економіці господарства. Щоб уникнути такого положення, оборотні кошти нормуються, що є ...
... не тільки до зниження ефективності виробництва плодово-ягідної продукції, а й загрожує повною ліквідацією галузі садівництва у Запорізькій області. 2.2 Ефективність виробництва плодово-ягідної продукції В умовах реформування аграрного сектора економіки й розвитку багатоукладності розв‘язання проблеми ефективного виробництва плодово-ягідної продукції зумовлює необхідність визначення напрямів ...
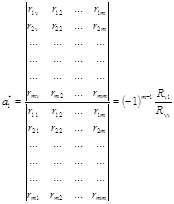
0 комментариев