Большие и сложные системы. Классификация систем по ресурсной обеспеченности управления

28. Большие и сложные системы. Классификация систем по ресурсной обеспеченности управления

Научно-техническая революция вызвала возникновение нового объекта исследований в области управления, получившего название «большие системы».

Важнейшими характерными чертами больших систем являются: целенаправленность и управляемость системы, наличие у всей системы общей цели и назначения, задаваемых и корректируемых в системах более высоких уровней; сложная иерархическая структура организации системы, предусматривающая сочетание централизованного управления с автономностью частей; большой размер системы, то есть большое число частей и элементов, входов и выходов, разнообразие выполняемых функций и т. д.; целостность и сложность поведения. Сложные, переплетающиеся взаимоотношения между переменными, включая петли обратной связи, приводят к тому, что изменение одной влечет изменение многих других переменных.

К большим системам относятся крупные производственно-экономические системы (например, холдинги), города, строительные и научно-исследовательские комплексы.

Подавляющее число экономических и управленческих задач имеет такой характер, когда уже заведомо можно сказать, что мы имеем дело с большими системами. Системный анализ предусматривает специальные приемы, с помощью которых большую систему, трудную для рассмотрения исследователем, можно было бы разделить на ряд малых взаимодействующих систем или подсистем. Таким образом, большой системой целесообразно назвать такую, которую невозможно исследовать иначе, как по подсистемам.

Помимо больших систем в задачах управления экономикой выделяют сложные системы.

Сложной целесообразно называть такую систему, которая строится для решения многоцелевой, многоаспектной задачи. Непосредственным выводом из концепции сложной системы для анализа и проектирования систем управления является требование учета следующих факторов:

1.         Наличие сложной, составной цели, параллельное существование разных целей или последовательная смена целей.

2.         Наличие одновременно многих структур у одной системы (например, технологической, административной, функциональной и т. д.).

3.         Невозможность описания системы в одном языке, необходимость использования спектра языков для анализа и проектирования отдельных ее подсистем.

Имеющиеся ресурсы не всегда обеспечивают качественное и своевременное решение по управлению. Обычно энергетические затраты на модель и выработку управления малы, но возможны ситуации, когда энергопотребление (при питании от общего ограниченного источника энергии) для управляемой и управляющей систем соизмеримы (космический аппарат, исследовательский робот, установки для экспериментов в ... частиц высоких энергий). Возникает для таких систем проблема наилучшего распределения ресурсов.

Материальные ресурсы - ресурсы ЭВМ при моделировании на ЭВМ - они лимитируют решение задач большой размерности в реальном масштабе времени (экономические, организационно-управленческие, ...).

Большие системы - системы, проблемы моделирования которых заключаются в их большой размерности (решение - декомпозиция или применение более мощных средств).

По информационному ресурсу: его достаточно для успешного управления - система простая. Если информации в системе не хватает для эффективного управления (непредвиденные, нежелательные результаты управлений), то система называется сложной. Сложность - это объективно существующее отклонение между управляемой системой и моделью в управляющей системе. Преодоление сложности - получить (после конкретной причины сложности) недостающую информацию или сменить цель.

Возможны комбинации разных типов (по ресурсам) систем:

1) малые простые /бытовые и справные приборы для пользователя/;

2) малые сложные /неисправные бытовые приборы для пользователя/;

3)большие простые /шифрозамок сейфа для похитителя, точный прогноз погоды, межотраслевой баланс/;

4) большие сложные /живой организм, мозг, экономика страны/.

  29. Распознавание больших и сложных систем.

Следует различать сложные и большие системы.

Сложная система – система с разветвленной структурой и значительным количеством взаимосвязанных и взаимодействующих элементов (подсистем), имеющих разные по своему типу связи, способная сохранять частичную работоспособность при отказе отдельных элементов (свойство робастности).

Сложная система - система, обладающая, по крайней мере, одним из перечисленных признаков:

а) допускает разбиение на подсистемы, изучение каждой из которых, с учетом влияния других подсистем в рамках поставленной задачи, имеет содержательный характер;

б) функционирует в условиях существенной неопределенности и воздействие среды на нее обусловливает случайный характер изменения ее параметров или структуры;

в) осуществляет целенаправленный выбор своего поведения.

Большая система – сложная система, имеющая ряд дополнительных признаков: наличие подсистем, имеющих собственное целевое назначение, подчиненное общему целевому назначению всей системы; большое число разнообразных связей (материальных, информационных, энергетических и т.п.); внешние связи с другими системами; наличие в системе элементов самоорганизации.

30. Способы перевода больших систем в малые, сложных в большие

 

Большой называется система, поведение которой определяется всей совокупностью ее элементов, взаимодействующих между собой, ни один из которых не является определяющим.

Сложной называется система, адекватное моделирование которой требует учета отсутствующей или недоступной информации.

Известны два способа перевода больших систем в разряд малых: использование более мощных вычислительных средств (компьютеров и программных систем) либо осуществление декомпозиции многомерной задачи на совокупность слабо связанных задач меньшей размерности (если характер задачи это позволяет). Если существует возможность сгруппировать элементы системы в незначительное количество подсистем, каждая из которых оказывает вполне определенное существенное влияние на поведение системы в целом, а с другими подсистемами мало взаимодействует, то этим самым описание функциональной структуры системы существенно упрощается.

На практике чаще всего исследователь самостоятельно решает неформализуемым путем, какие факторы он будет исследовать, а какие нет.

Между большими и сложными системами имеется много общего: очень часто большие системы одновременно являются и сложными. Но есть и существенное различие между ними: адекватное моделирование больших систем оказывается возможным при удовлетворении высоких требований к инструментам обработки (компьютерам и программным системам), тогда как при моделировании сложных систем возникают более фундаментальные проблемы, связанные с недостатком значимой информации.

31. Информация как свойство материи, сигналы в системах. Код, шум, сигнал

В связи с рассмотрением понятия модели отмечалось, что объединяющим все разновидности моделей, признаком является информационная сущность, любая модель несет информацию о свойствах и характеристиках оригинала, существенных для решаемой субъектом задачи.

Современное понимание информации (что это такое и ее роль) складывается как совокупность знаний, полученных конкретными науками (физика, биология, теория связи, ...) и философских обобщений.

Обычный смысл слова информация: "сведения, известия, сообщения, знания" трактует информацию как нечто, присущее только человеку, человеческому сознанию и общению. Материалистическая теория познания связывает наше знание с определением реального мира, соединяя отражение реального мира в нашем сознании с отображением, как всеобщим свойством материи. Некоторые ученые трактуют при этом свойство отражения как свойство материи обладать информацией, рассматривая информацию как всеобщее изначально присущее материи свойств.

Наряду с такой атрибутивной точкой зрения, существует функциональный подход к понятию информации, связывающий ее с управлением, и, следовательно, относящий информацию только к системам управления, которые существуют в живой природе, технике, обществе. В этом смысле понятие информации является основным для кибернетики - науки об управлении и связи.

Информация в системе управления возникает при обработке сигналов, поступивших из внешней среды. В качестве сигналов используются состояния некоторых объектов (каналов связи), соответствующим определенным состояниям управляемого объекта и внешней среды. Кроме этого, на состояние каналов связи влияют и другие объекты и системы из внешней среды, несущественные с точки зрения целей системы управления. Это воздействия являются помехами или шумами. При изучении каналов связи и их свойств можно рассматривать их в достаточной степени автономно, отвлекаясь от системы управления в которую они входят и говорить, что сами сигналы - это и есть информация, передаваемая посредством этого канала. Канал - носитель информации, передающий ее во времени и пространстве. Для образования сигналов могут быть использованы только объекты, состояния которых достаточно устойчивы, во времени или по изменению положения в пространстве.

В связи с этим сигналы делятся на два типа:

1). Стабильные состояния физических объектов (книга, фотография, маг. запись) - статические сигналы.

2). Динамические состояния физических полей. Изменение их состояния не локализовано (в неизолированной части поля) и приводит к распространению возмущения. Конфигурация этого возмущения обладает определенной устойчивостью, что обеспечивает сохранение сигнала (звук - колебания в газе, твердом теле, жидкости, радиосигналы, электромагнитного поля), такие сигналы называются динамическими. Н. Винер: общество простирается до тех пределов, до каких распространяется информация.

  32. Типы сигналов. Случайный процесс – математическая модель сигналов

Сигналы делятся на два типа:

1). Стабильные состояния физических объектов (книга, фотография, магнитофонная запись) - статические сигналы.

2). Динамические состояния физических полей.

Изменение их состояния не локализовано (в неизолированной части поля) и приводит к распространению возмущения. Конфигурация этого возмущения обладает определенной устойчивостью, что обеспечивает сохранение сигнала (звук - колебания в газе, твердом теле, жидкости, радиосигналы, ... электромагнитного поля), такие сигналы называются динамическими. Н. Винер: общество простирается до тех пределов, до каких распространяется информация.

Математические модели случайных процессов широко используются как для описания полезных сигналов, так и сигналов помех. Наиболее известной моделью случайного процесса является гауссовский случайный процесс.

Случайный процесс (вероятностный, или стохастический), процесс изменения во времени состояния или характеристик некоторой системы под влиянием различных случайных факторов, для которого определена вероятность того или иного его течения.

  33. Эксперимент и модель. Современное понятие эксперимента

Эксперимент (от лат. experimentum - проба, опыт), метод познания, при помощи которого в контролируемых и управляемых условиях исследуются явления природы и общества.

Научное исследование реального процесса можно проводить теоретически или экспериментально, которые проводятся независимо друг от друга. Такой путь познания истины носит односторонний характер. В современных условиях развития науки и техники стараются проводить комплексное исследование объекта. Этого можно добиться на основе новой, удовлетворяющей требованиям времени, методологии и технологии научных исследований.

Рассмотрим связь модели и эксперимента на примере вычислительного эксперимента.

Вычислительный эксперимент - это эксперимент над математической моделью объекта на ЭВМ, который состоит в том, что по одним параметрам модели вычисляются другие её параметры и на этой основе делаются выводы о свойствах явления, описываемого математической моделью. В проведении вычислительного эксперимента участвует коллектив исследователей - специалисты с конкретной предметной области, математики теоретики, вычислители, прикладники, программисты. Это связано с тем, что моделирование реальных объектов на ЭВМ включает в себя большой объём работ по исследованию их физической и математической моделей, вычислительных алгоритмов, программированию и обработке результатов. Здесь можно заметить аналогию с работами по проведению натурных экспериментов: составление программы экспериментов, создание экспериментальной установки, выполнение контрольных экспериментов, проведение серийных опытов, обработки экспериментальных данных и их интерпретация и т.д. Таким образом, проведение крупных комплексных расчётов следует рассматривать как эксперимент, проводимый на ЭВМ или вычислительный эксперимент.

Задача проектирования, например, сети обслуживания должна решаться с позиций системного подхода, учитывающего ее многоаспектность и иерархичность. Естественно, что те же свойства приобретает и процесс проектирования, проходящий уже на фазе моделирования несколько этапов и требующий применения разнообразного математического аппарата. В процессе имитационного эксперимента над моделью с учетом случайных исходов необходимо:

·           классифицировать факторы на существенные и несущественные;

·           разделить и оценить количественно влияния факторов и их комбинаций на целевую функцию;

·           найти наивыгоднейшую комбинацию факторов.

Структура эксперимента (количество прогонов, выбор исходных данных для них и характер обработки результатов) определяется его целью. Первая проблема решается средствами дисперсионного анализа, вторая – регрессионного и факторного (скрининг), третья - методами статистической оптимизации.

34. Измерение, измерительные шкалы

Одной из задач при выработке решений является измерение рассматриваемых критериев по выбранным шкалам.

Под формированием шкалы понимается присвоение объектам (вещам, предметам или событиям) чисел согласно некоторой системе правил.

Можно выделить четыре уровня измерения и соответственно четыре типа шкал:

- шкалы наименований;

- шкалы порядка;

- шкалы интервалов;

- шкалы отношений.

В шкале наименований число используется как название или классификация. Можно нумеровать альтернативы, объекты, действия и т.д. Это не будет означать ничего иного, кроме того, что каждый отдельный предмет должен иметь различное обозначение. На шкалах наименований допустимы некоторые статистические операции. Можно, например, определить число элементов, принадлежащих какому-либо классу, найти наиболее многочисленный класс.

Шкалы порядка формируются в том случае, когда есть возможность сравнения двух объектов по общему признаку. Шкалы могут быть простого и слабого порядков. В шкалах простого порядка каждый элемент должен иметь более высокий или более низкий ранг, чем всякий другой элемент. Элементы на шкале слабого порядка могут иметь равную оценку. Поскольку элементы на шкалах порядка могут быть расположены неравномерно, то не допускается использование каких-либо арифметических операций. Возможно использование тех же статистических операций, что и на шкалах наименований и, кроме того, можно вычислить медианы, центили, коэффициенты ранговой корреляции.

Шкалы интервалов иначе называют равномерными; числено равные разности выражают эмпирически равные разности в измеряемом общем признаке. Шкалы интервалов не обладают свойством аддитивности; и, следовательно, в общем случае, на них нельзя осуществлять арифметические операции. Однако, при введении произвольного нуля, разности на шкалах интервалов можно рассматривать как абсолютные величины и производить с ними арифметические действия. Примером измерения в шкалах интервалов может служить календарное время или высота над уровнем моря. Для шкал интервалов приемлемы те же статистические операции, что и для шкал более низкого уровня, а также возможно вычисление математического ожидания, стандартного отклонения, смешанных моментов и коэффициента асимметрии.

Шкала отношений обладает всеми свойствами других шкал и, кроме этого, свойством аддитивности, что делает возможным проведение любых статистических и арифметических операций. В шкалах отношений измеряются любые физические величины; нуль шкалы естественен.

В задачах многокритериального ПР возникает необходимость формирования отдельных шкал для измерения разных компонентов рассматриваемого свойства. Такая шкала называется многомерной. При этом критерии в многомерной шкале могут измеряться по шкалам как одного, так и разных уровней.

35.Модели обработки данных, типичные задачи, классификационных и числовых моделей

Одной из важных задач искусственного интеллекта является задача обобщения информации. Благодаря применению методов извлечения и обобщения информации в системах принятия решений возможно построение обобщенных моделей данных и обработка больших массивов экспериментальных данных, полученных в ходе различного рода процессов и явлений. Источники таких больших потоков данных имеются во многих областях: банковское дело, розничная торговля, управление и диагностика, маркетинг и т.д. Общим для всех этих данных является то, что они содержат большое количество скрытых закономерностей, являющихся весьма важными для принятия стратегических решений. Для выявления этих закономерностей и используются методы обобщения и компьютерные системы, реализующие эти методы.

Большинство специалистов по обработке экспериментальных данных сходятся в том, что разнообразные задачи анализа информации могут быть сведены к трем: классификации исходных данных, выбору информативных признаков, идентификации неизвестных наблюдений.

Схема информационных преобразований данных в классификационной задаче приведена на рис.1.

В общем случае эмпирические данные могут быть сведены в таблицу . Используя различные модели , лежащие в основе методов классификации, исследователь преобразует описание таблицы в вид адекватный этим моделям. В рамках геометрической модели таблицу можно представить в виде совокупности “векторов – строк” (объектов) в признаковом пространстве . Структура “векторов – строк” меняется в зависимости от моделей описания данных . В качестве описаний могут выступать матрицы близости, сходства, подобия.

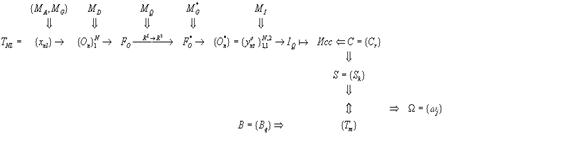
Рис.1

Классический подход к оценке информативности параметров исходного описания данных в задаче классификации сводится к следующей процедуре:

- по всей совокупности параметров в рамках конкретного решающего правила оценивается ошибка классификации ;

- из исходной совокупности параметров

изымается параметр и повторно оценивается ошибка классификации ;

- путем сравнения этих ошибок и определения их разности :

выносится суждение о роли параметра в классификационной задаче. Так, если > 0, то параметр является “вредным” для классификации. Если < 0, то параметр – “полезен”, а, если =0, то “бесполезен”. Такой подход определяет необходимость последовательного перебора всех параметров, а также их возможных сочетаний, что влечет за собой значительные временные затраты.

36. Выбор как реализации цели. Определение термина «выбор»

Определение: принятие решения ("выбор") есть действие над множеством альтернатив, в результате которого исходное множество альтернатив сужается, т.е. происходит его редукция.

Выбор является действием, придающим всей деятельности целенаправленность. Именно через акты выбора реализуется подчиненность всей деятельности определенной цели или совокупности взаимосвязанных целей.

Принятие решений как снятие неопределенности (информационный подход).

Процесс получения информации можно рассматривать как уменьшение неопределенности в результате приема сигнала, а количество информации – как количественную меру степени снятия неопределенности.

Но в результате выбора некоторого подмножества альтернатив из множества, т.е. в результате принятия решения, происходит тоже самое (уменьшение неопределенности).

Это значит, что каждый выбор, каждое решение порождает определенное количество информации, а значит может быть описано в терминах теории информации.

К настоящему моменту сложилось три основных языка описания задач выбора. Самым простым, наиболее развитым является критериальный язык. Второй, более общий язык, на котором описывается выбор, - это язык

бинарных отношений. Основные предположения этого языка сводятся к следующему:

- отдельная альтернатива не оценивается, т.е. критериальная функция не вводится;

- для каждой пары альтернатив можно установить, что одна из них либо предпочтительнее другой, либо они равноценны или не сравнимы;

- отношения предпочтения внутри любой пары альтернатив не зависит от остальных альтернатив.

Бинарные отношения могут быть заданы через описание пар, с помощью матрицы предложений, через граф предпочтений или сечелиями.

Третьим языком описания выбора является язык функций выбора. Он описывает выбор как операцию над произвольным множеством альтернатив, которая ставит этому множеству в соответствие некоторое его подмножество.

Такое соответствие двух множеств без их поэлементного соответствия значительно расширяет смысл термина “функция”.

Таким образом, в настоящее время известно большое количество разнообразных методов ПР и различных подходов к их классификации. При использовании разных методов решения задачи можно получить прямо противоположные результаты при одной и той же исходной информации. В связи с этим возникает проблема выбора метода (методов), подходящих для решения конкретной задачи принятия решений.

37. Множественность задач выбора. Критериальный язык описания выбора

Множественность задач принятия решений связана с тем, что каждая компонента ситуации, в которой осуществляется принятие решений, может реализовываться в качественно различных вариантах

Критериальный язык принятия решений.

Об одном и том же явлении можно говорить на различных языках различной степени общности и адекватности. К настоящему времени сложились три основных языка описания выбора.

Самым простым, наиболее развитым и наиболее популярным является критериальный язык

Название этого языка связано с основным предположением, состоящим в том, что каждую отдельно взятую альтернативу можно оценить некоторым конкретным (одним) числом, после чего сравнение альтернатив сводится к сравнению соответствующих им чисел.

Пусть, например, {X} – множество альтернатив, а x – некоторая определенная альтернатива, принадлежащая этому множеству: xX. Тогда считается, что для всех x может быть задана функция q(x), которая называется критерием (критерием качества, целевой функцией, функцией предпочтения, функцией полезности и т.п.), обладающая тем свойством, что если альтернатива x1 предпочтительнее x2 (обозначается: x1 > x2), то q(x1)>q(x2).

При этом выбор сводится к отысканию альтернативы с наибольшим значением критериальной функции.

Однако на практике использование лишь одного критерия для сравнения степени предпочтительности альтернатив оказывается неоправданным упрощением, так как более подробное рассмотрение альтернатив приводит к необходимости оценивать их не по одному, а по многим критериям, которые могут иметь различную природу и качественно отличаться друг от друга.

Многокритериальные задачи не имеют однозначного общего решения. Поэтому предлагается множество способов придать многокритериальной задаче частный вид, допускающий единственное общее решение. Естественно, что для разных способов эти решения являются в общем случае различными. Поэтому едва ли не главное в решении многокритериальной задачи – обоснование данного вида ее постановки. Используются различные варианты упрощения многокритериальной задачи выбора, основным из которых является сведение многокритериальной задачи к однокритериальной путем ввода интегрального критерия.

Основная проблема в многокритериальной постановке задачи принятия решений состоит в том, что необходимо найти такой аналитический вид функции, связывающей частные критерии с интегральным критерием, который бы обеспечил следующие свойства модели: высокую степень адекватности предметной области и точке зрения экспертов; минимальные вычислительные трудности максимизации интегрального критерия, т.е. его расчета для разных альтернатив; устойчивость результатов максимизации интегрального критерия от малых возмущений исходных данных.

38. Описание выбора на языке бинарных отношений, как математического объекта

Более общий язык, на котором описывается выбор, - это язык

бинарных отношений.

Основные предположения этого языка сводятся к следующему:

- отдельная альтернатива не оценивается, т.е. критериальная функция не вводится;

- для каждой пары альтернатив можно установить, что одна из них либо предпочтительнее другой, либо они равноценны или не сравнимы;

- отношения предпочтения внутри любой пары альтернатив не зависит от остальных альтернатив.

Бинарные отношения могут быть заданы через описание пар, с помощью матрицы предложений, через граф предпочтений или сечелиями.

39. Групповой выбор. Правила «статистической» техники безопасности

Пусть имеется группа лиц, имеющих право принимать участие в коллективном принятии решений. Предположим, что эта группа рассматривает некоторый набор альтернатив, и каждый член группы осуществляет свой выбор. Ставится задача о выработке решения, которое определенным образом согласует индивидуальные выборы и в каком-то смысле выражает "общее мнение" группы, т.е. принимается за групповой выбор.

Естественно, различным принципам согласования индивидуальных решений будут соответствовать различные групповые решения.

Правила согласования индивидуальных решений при групповом выборе называются правилами голосования. Наиболее распространенным является "правило большинства", при котором за групповое решение принимается альтернатива, получившая наибольшее число голосов.

Необходимо понимать, что такое решение отражает лишь распространенность различных точек зрения в группе, а не действительно оптимальный вариант, за который вообще никто может и не проголосовать. "Истина не определяется путем голосования", самой распространенной точкой зрения может быть и заблуждение.

Кроме того, существуют так называемые "парадоксы голосования", наиболее известный из которых парадокс Эрроу.

Эти парадоксы могут привести, и иногда действительно приводят, к очень неприятным особенностям процедуры голосования: например бывают случаи, когда группа вообще не может принять единственного решения (нет кворума или каждый голосует за свой уникальный вариант, и т.д.), а иногда (при многоступенчатом голосовании) меньшинство может навязать свою волю большинству, как это было на президентских выборах в США "Буш – Гор".

Оставив в стороне человеческий фактор (например, недобросовестный или субъективный отбор данных), можно выделить несколько правил "статистической техники безопасности", связанных с самой природой статистических выводов.

Данные должны иметь действительно случайную природу (обладать статистической устойчивостью), что далеко не всегда имеет место, и очень непросто проверяемо.

Закономерность, выявленная статистически, никогда не бывает абсолютно точной: числовая характеристика всегда оценивается лишь приближенно; вероятность ошибки статистического вывода всегда отлична от нуля (ошибки первого и второго родов).

В структуре любого алгоритма статистической обработки данных заложены априорные предположения о природе данных. Если эти предположения расходятся с тем, что есть на самом деле, выводы получаются совсем не такого качества, которое от них ожидается. Практики же редко проверяют выполнимость "паспортных" ограничений на применимость процедур.

Выявленная статистическая закономерность подлежит содержательной интерпретации. Статистику нельзя обвинять за то, что вполне надежный статистический вывод неверно проинтерпретирован специалистом - пользователем; последний же часто "пеняет на зеркало".