Операции, входящие в состав сетевых графиков

2.2 Операции, входящие в состав сетевых графиков

Параллельные операции. Предположим, что между двумя событиями Еi и Еj находятся две различные операции b и с, следующие за операцией а.

Введем тогда фиктивное событие Еj и дополнительную фиктивную операцию х между Еi и Еj. В случае, когда имеется три, четыре и т. д. параллельные операции, поступают так же, вводя для каждой из них фиктивное событие и дополнительную фиктивную операцию, как это показано на рисунке 2.6.

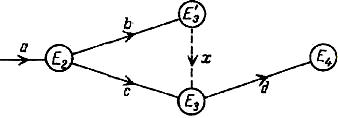
Рисунок 2.6 – Параллельные операции в сетевой модели

Операции зависимые и независимые. Рассмотрим на рисунке 2.7 операции с и d, следующие за а и b. Предположим теперь, что с следует за а и b, но d следует только за b и не обязано следовать за а. В этом случае уже нельзя пользоваться данной сетью и необходимо ввести событие Е'₃ и фиктивную операцию х, как это показано на рисунке 2.8.

Рисунок 2.7 – Зависимые операции

Рисунок 2.8 – Независимые операции

2.3 Особые ограничения. Критический путь. Резерв времени

Предположим, что некоторая операция может быть начата только по наступлении какого–то момента, т. е. по прошествии некоторого срока после события Е₁ принимаемого за начальное [13, с. 124]. Такое ограничение выражается введением фиктивной операции z между Е₁ и событием Еi, где начинается рассматриваемая операция. Это показано на рисунке 2.9.

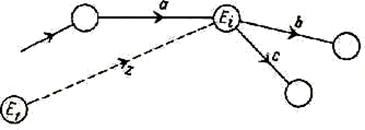
Рисунок 2.9 – Ограничение с одной фиктивной операцией

Рисунки 2.10 и 2.11 относятся к случаю, когда приходится вводить две фиктивные операции x и z: операция с, следующая за а, должна быть отсрочена на время z.

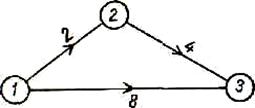
Рисунок 2.10 – Ограничение с двумя фиктивными операциями

Рисунок 2.11 – Критический путь

Во многих задачах встречаются некоторые «условия отсрочки начала выполнения операции»; ими могут быть, например, сроки поставки материалов, климатические условия и т. п. Как мы видим, такие особые условия легко могут быть введены в сеть.

Для того чтобы иметь возможность учесть такие ограничения и ввести их в сеть, сформулируем их по–другому: «Для того чтобы некоторая работа j могла быть начата, необходимо, чтобы время, прошедшее с момента начала другой работы j, было не меньше данного (–t_ij)»; это приводит к обычным связям, но с отрицательной длительностью (длина соответствующей дуги будет отрицательна), что необязательно означает усложнение решения задачи.

Теперь займемся сроком завершения всех работ, и это подведет нас к основному содержанию настоящей работы – методу критического пути.

Время завершения комплекса операций. Критический путь. Когда сеть проекта построена, встает следующий вопрос: каково время завершения всего комплекса операций, т. е. какова продолжительность реализации проекта. Это время не может быть меньше суммы длительностей операций, взятой вдоль «самого неблагоприятного пути» из Е₁ в Е_n, т. е. вдоль такого пути между этими двумя точками, который дает максимальную сумму длительностей операций. Такой путь (их может оказаться несколько) называется «критическим путем».

Беря в качестве продолжительности выполнения комплекса работ сумму длительностей операции вдоль «наименее благоприятного пути из Е₁ в Е_n», мы тем самым обеспечиваем возможность действительного выполнения всех намеченных операций с учетом их длительностей [13, с. 136].

Одна из математических формулировок, позволяющая решить эту проблему, изложена ниже.

Начиная с события Е₁, которому припишем время наступления 0, рассмотрим для каждой вершины сети дуги, которые в нее входят; для каждой из этих дуг сложим время соответствующей операции, которое приписано дуге, с временем наступления события, соответствующего началу дуги; сравнивая результаты и выбирая из них наибольший, приписываем его рассматриваемой вершине.

Рассмотрим рисунок 2.11. В Е₂ входит только одна дуга (1,2). Поскольку для Е₁ имеем 0, то для Е₂ получим 0+8=8. В Е₃ входят две дуги (2,3) и (1,3); сравнивая 8+4=12 с 0+13=13, приписываем Е₃ значение 13; это означает, что наступление события Е₃ нельзя ожидать раньше 13. В Е₄ входят две дуги (3,4) и (1,4); сравнивая 13+7=20 с 0+9=9, приписываем Е₄ значение 20. Е₅ приписываем значение 17. В Е₆ входят две дуги (2,6) и (3,6); сравнивая 8+ 6=14 с 13+10=23, приписываем Е₆ значение 23. В Е₈ входят три дуги (6,8), (3,8) и (4,8); сравнивая 23+3=26, 13+6=19 и 20+9=29, приписываем Е₈ значение 29. Так продолжаем вплоть до события Еn, которому приписываем окончательно значение 61.

Это число представляет собой время выполнения проекта, начинающегося с нулевого момента. Путь, соответствующий этому времени в 61 единицу, легко получить, возвращаясь шаг за шагом обратно из Е₁₂ в Е₁; это и будет критический путь. На рисунке 19 он отмечен жирной линией.

Если проект (комплекс операций) будет разворачиваться без неожиданных нарушений, его продолжительность должна будет составить 61 неделю и соответствующие события произойдут в моменты, указанные на рисунке 19.

Операции P₁₃, P₃₄, P₄₈, P_8,11, P_11,10, P_10,12 называются «критическими операциями». С них нужно начинать работу после наступления начальных событий соответствующих дуг. Так, к примеру, операция Р₄₈ должна начаться в первую очередь после реализации события Е₄, т. е. в момент 20. Если критическая операция будет задержана, это вызовет запаздывание выполнения всего проекта. Например, если операция Р₄₈ начнется только в момент 22, проект будет завершен не раньше, чем к моменту 63.

Таким образом, критические операции представляют собой те операции проекта, на ход выполнения которых руководитель должен направить все свое внимание, так как от их своевременного выполнения зависит общий срок завершения всего проекта (всего комплекса работ). «Некритические операции» допускают некоторое запаздывание в выполнении операций.

Резервный интервал события. Резервы времени операций. Выше установили времена наступления различных событий, составляющих сеть проекта.

Для каждого некритического события Еi важно знать предельный срок его наступления, т. е. срок, превышение которого приведет к задержке выполнения всего проекта [13, с. 142].

Рассмотрим для этого событие Еi. Минимальное время, необходимое для наступления всех событий, расположенных между событиями Еi и Еn, получается определением в сети «самого длинного» пути от Еi до Еn. Эта процедура обеспечивает нам уверенность в возможности действительного выполнения операций, следующих за Еi с учетом соответствующих им длительностей. Искомый предельный срок t_i^* получается вычитанием этого минимального времени из времени t_n наступления конечного события Е_n.

Таким образом, для каждого некритического события мы получаем два граничных срока:

– время t_i: ожидаемое время наступления события Еi;

– время t_i^1*: предельное время наступления события Еi,превышение которого приведет к изменению общего времени завершения всего комплекса операций.

Для критических событий предельный срок t_i^* совпадает с ожидаемым временем t_i. Эти события не допускают никакого запаздывания в сроках их наступления, или (что означает то же самое) критические операции не допускают никакой задержки в их выполнении.

Интервал (t_i,, t^*_i) называется интервалом свободы события (резервным интервалом). Это, таким образом, интервал времени, в течение которого может наступить событие Ei без изменения общего времени завершения всех работ.

Обратимся опять к примеру капитального ремонта электровоза в аппаратном цехе и вычислим граничные сроки t^*_i, используя тот же метод, как и при вычислении t_i но отправляясь на этот раз от конечного события Е_12.

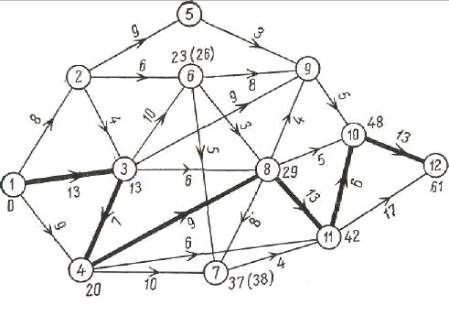
Рисунок 2.12 – Свободный резервный интервал

Рассмотрим рисунок 2.12. Сначала событие Е₇, изображенное, отделенное от события Е₁₁ операцией длительностью 4, так что операция Р₇,₁₁ и может начаться за четыре недели до события Е₁₁ и, следовательно, событие Е₇ должно произойти в интервале [37, 38]. Событие Е₉ отделено от события Е₁₀ операцией длительностью 5, так что операция Р₉,₁₀ может начаться за пять недель до события Е₁₀ и поэтому событие Е₉, должно произойти в интервале [33,43]. Событие Е₆ отделяет от события Е₉, операция в 8 недель, от события Е₈ – 3 недели, от события Е₇ – 5 недель; из сравнения 43–8=35, 29–3 =26 и 38–5=33 видно, что событие Е₆ должно произойти не позднее момента 26 (наименьшее из трех), чтобы не вызвать нарушений, которые отразились бы на завершающей дате. Числа, которые при этом получаются, выписаны на рисунке 20 и заключены в скобки, чтобы не путать их с теми числами, которые были получены при на хождении критического пути. Событию Е₅ припишем (40); событию Е₂ после сравнения 40–9=31, 26–6=20, 13–4=9 припишем (9).

Подводя итоги, можно сказать, что моменты наступления событий Еi могут находиться в приведенных ниже интервалах (от–до), причем на критическом пути эти интервалы сводятся к точным датам:

E₁ : 0

Е₂ : (8,9)

Е₃ : 13

Е₄ : 20

Е₅ : (17,40)

Е₆ : (23,26)

Е₇ : (37,38)

Е₈ : 29

Е₉ : (33,43)

Е₁₀ : 48

Е₁₁ : 42

Е₁₂ : 61

Точно так же интересно знать для каждой операции Рij, какая задержка может быть допущена при ее выполнении без того, чтобы это привело к нарушению срока наступления события Еj. Эта возможная отсрочка начала выполнения операции Рij есть «свободный резерв времени» операции Рij, обозначаемый в дальнейшем через Мij.

Если t_i и t_j – ожидаемые сроки наступлений событий Еi и Еj, между которыми имеется операция Рij длительностью t_ij, то ее свободный резерв времени равен Mij=t_j-t_i-t_ij.

Свободный резерв времени критических операций равен нулю, так как в отношении этих операций не может быть допущена никакая отсрочка в начале их выполнения.

Таким же образом определяются для каждой операции «полный резерв времени» и «независимый резерв времени».

По определению полный резерв времени операции Рij равен

t^*_j–t_i–t_ij,

а ее независимый резерв времени равен

t_j–t^*_i–t_ij¹.

Резервы событий и операций характеризуют эластичность проекта. Чем более они уменьшаются, тем жестче сеть проекта. Сеть проекта «полной жесткости» такова, что все ее пути являются критическими. В ней нет ни резервов событий, ни свободных резервов операций. При таком положении недопустимы никакие задержки, ни по какой из операций.

Существенное различие между резервом события Еi и свободным или полным резервом операции Рij состоит в том, что резерв события представляет собой запаздывание, которое может быть допущено в наступлении события Еi без изменения фиксированных сроков наступления критических событий, и в частности конечного события, соответствующего выполнению проекта, в то время как свободный резерв операции Мij представляет собой отсрочку начала выполнения операции Рij, без изменения ожидаемого срока наступления события Ej, а полный резерв представляет собой максимальную допустимую отсрочку начала выполнения этой операции.

Другой аспект понятия свободный резерв может быть выявлен в случае, когда продолжительность некритических операций может быть удлинена. В этом случае свободный резерв Мij соответствует возможному удлинению длительности операции Pij, оставляющему неизменными сроки t_i и t_j наступления событий Ei и Ej, определяющих эту операцию.

Эта разница между резервом события и свободным резервом или полным резервом операции лучше всего видна в сети, изображенной на рисунке 2.12 и воспроизведенной на рисунке 2.13.

Рисунок 2.13 – Полный резерв

Здесь интервал свободы события Е₆ есть (23, 26). Свободный резерв операции Р₆₉ равен М₆₉ = 33-23-8=2.

Следовательно, операция Р₆₉ может начаться в момент 23+2=25 без изменения времени t₉ – срока наступления события Е₉, который остается равным 33.

Свободные резервы операций указаны на рисунке 2.13 в скобках.

Полный резерв операции P₆₉ равен 43-23-8=12. Таким образом, операция P₆₉ может начаться в момент 23+12=35, не вызывая задержку выполнения всего комплекса работ.

Важное значение понятий граничных сроков событий и свободных резервов операций особенно дает себя знать в процессе выполнения проекта. Если все события наступают в пределах граничных сроков t^*_i то проект осуществляется нормально и конечный срок t_n будет выдержан. Если, напротив, по каким–либо причинам случится, что момент наступления некоторого события превысит предельный срок t^*_I, то руководители проекта должны произвести, если это возможно, перераспределение сил, чтобы ускорить работы в этой части выполнения проекта. Если такой возможности нет, то можно утверждать, что срок выполнения всего комплекса операций будет задержан, и эту задержку можно вычислить.

Граничные сроки событий представляют собой, таким образом, «пределы безопасности» и являются для руководителя «сигналом тревоги», предупреждающим о срыве срока выполнения проекта [13, с. 155; 6, с. 206].

В некоторых исследованиях в качестве критерия приоритета используется свободный резерв, но обычно, когда речь идет о том, как приступить к делу и проверить способы организации работ, в качестве критерия приоритета выбирается полный резерв; этот критерий принимается в расчет чаще всего.

ГлавА 3 Применение системы СПУ при ремонте электровозов

Похожие работы

Ценообразование на предприятии железнодорожного транспорта в современных условиях

Скачать

45158

0

0

... и др. С экономической точки зрения, наиболее правильной является своевременная и полная оплата перевозок грузовладельцами, а также своевременная и полная оплата железнодорожным транспортом потребляемыx в процессе его деятельности ресурсов. В современных условиях эти требования выполняются не полностью, хотя вплоть до конца 1999 г. имела место положительная тенденция повышения доли "живых денег" ...

Финансов предприятий железнодорожного транспорта

Скачать

27512

3

0

... возможностей основных производственных фондов дороги является их производственная мощность. Производственная мощность – это максимально возможный выпуск продукции в единицу времени. Для разных подразделений железнодорожного транспорта производственная мощность измеряется в разных единицах. Для транспортных линий в целом – это пропускная (провозная) способность, сортировочных горок – число ...

Диспетчерское управление на железнодорожном транспорте

Скачать

26921

0

3

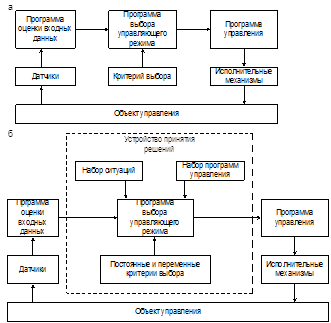
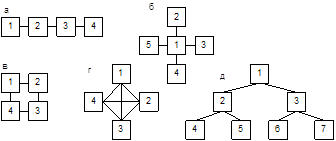
... Этим выражается направленность передачи управляющей и контрольной информации между подсистемами. Часто структура выражает только соотношение между подсистемами по управлению (подчиненность). В диспетчерском управлении железнодорожным транспортом получили распространение иерархические централизованные структуры (рис. 1.2, д). В этом случае каждый более высокий уровень управления имеет радиальные ...

Эксплуатационные расходы на железнодорожном транспорте

Скачать

45701

4

0

... , пассажиров, багажа и почты. Планирование эксплуатационных расходов железных дорог производится по однородным видам затрат, т.е. по экономическим элементам. Наибольший удельный вес в эксплуатационных расходах железнодорожного транспорта занимают расходы по оплате труда. Фонд оплаты труда планируется, исходя из лимита численности персонала, занятого в перёвозках, и среднемесячной заработной ...