Навигация
Ухвалення рішень в умовах ризику
2. Ухвалення рішень в умовах ризику
Якщо рішення ухвалюється в умовах ризику, то вартості альтернативних рішень звичайно описуються розподілами вірогідності. З цієї причини ухвалюване рішення ґрунтується на використовуванні критерію очікуваного значення, відповідно до якого альтернативні рішення порівнюються з погляду максимізації очікуваного прибутку або мінімізації очікуваних витрат. Такий підхід має свої недоліки, які не дозволяють використовувати його в деяких ситуаціях. Для них розроблені модифікації згаданого критерію. Тут розглядаються часто використовувані підходи до ухвалення рішень в умовах ризику.
2.1 Критерій очікуваного значення
Критерій очікуваного значення зводиться або до максимізації очікуваного (середньої) прибутку, або до мінімізації очікуваних витрат. В даному випадку передбачається, що прибуток (витрати), пов'язаний з кожним альтернативним рішенням, є випадковою величиною.
Дерево рішень.
У приведеному нижче прикладі розглядається проста ситуація, пов'язана з ухваленням рішення за наявності кінцевого числа альтернатив і точних значень матриці доходів.
Приклад 1.
Припустимо, що ви хочете вкласти на фондовій біржі 10 000 доларів в акції однієї з двох компаній: А або В. Акції компанії А є ризикованими, але можуть принести 50% прибутку від суми інвестиції впродовж наступного року. Якщо умови фондової біржі будуть несприятливі, сума інвестиції може знецінитися на 20%. Компанія В забезпечує безпеку інвестицій з 15% прибутку в умовах підвищення котирувань на біржі і лише 5% - в умовах пониження котирувань. Всі аналітичні публікації, з якими можна познайомитися (а вони завжди є удосталь в кінці року), з вірогідністю 60% прогнозують підвищення котирувань і з вірогідністю 40% - пониження котирувань. У яку компанію слід вкласти гроші?
Інформація, пов'язана з ухваленням рішення, підсумовувана в наступній таблиці 1.
| Альтернативне рішення | Прибуток від інвестиції за один рік | |
| При підвищенні | При пониженні | |
| котирувань (дол.) | котирувань (дол.) | |
| Акції компанії А | 5000 | -2000 |
| Акції компанії В | 1500 | 500 |
| Вірогідність події | 0.6 | 0.4 |
Виходячи з схеми таблиці 1, одержуємо очікуваний прибуток за рік для кожної з двох альтернатив.
Для акцій компанії А: $5000 х 0.6 + (-2000) х 0.4 = $2 200. Для акцій компанії В: $1500 х 0.6 + $500 х 0.4 = $1 100.
Вашим рішенням, заснованим на цих обчисленнях, є покупка акцій компанії А.
У теорії ухвалення рішень підвищення і пониження котирувань на біржі іменуються станами природи, можливі реалізації яких є випадковими подіями (в даному випадку з вірогідністю 0.6 і 0.4). У загальному випадку задача ухвалення рішень може включати n станів природи і m альтернатив. Якщо pj - вірогідність j-го стану природи, а aij - платіж, пов'язаний з ухваленням рішення i при стані природи j (i = 1, 2,..., m; j = 1, 2,..., n), тоді очікуваний платіж для вирішення i обчислюється у вигляді,
![]()
де за визначенням p1+p2+…+pn=1.
Якнайкращим рішенням буде те, яке відповідає ![]() або
або ![]() , залежно від того, чи є платіж в задачі доходом (прибутком) або збитком (витратами).
, залежно від того, чи є платіж в задачі доходом (прибутком) або збитком (витратами).
2.2 Складніші ситуації ухвалення рішень
Для демонстрації інших можливостей застосування критерію очікуваного значення розглянемо ситуації ухвалення рішень, в яких платня є математичною функцією альтернативних рішень. В цьому випадку представлення задачі у вигляді дерева рішень хоча і є можливим, але може бути не таким корисним, як в попередніх прикладах.
Приклад 2.
Електроенергетична компанія використовує парк з 20 вантажних автомобілів для обслуговування електричної мережі. Компанія планує періодичний профілактичний ремонт автомобілів. Вірогідність pt поломки автомобіля після закінчення t місяців після профілактичного ремонту оцінюється таким чином.
Таблиця 2.
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ≥10 |
| pt | 0.05 | 0.07 | 0.1 | 0.13 | 0.18 | 0.23 | 0.33 | 0.43 | 0.5 | 0.55 |
Випадкова поломка одного вантажного автомобіля обходиться компанії в 200 доларів, а планований профілактичний ремонт в 50 доларів. Необхідно визначити оптимальний період (у місяцях) між планованими профілактичними ремонтами. Позначимо через N шукане число місяців між профілактичними ремонтами. Впродовж N-місячного циклу можуть мати місце два види витрат:
1) витрати, пов'язані з усуненням поломки автомобіля впродовж перших N-1 місяців;
2) витрати на профілактичний ремонт в кінці циклу.
Витрати другого вигляду (профілактичний ремонт) складають $50х20 автомобілів, тобто 1000 доларів на цикл. Витрати, пов'язані з усуненням поломок автомобілів, повинні ґрунтуватися на середній кількості автомобілів, що вийшли з ладу впродовж перших N-1 місяців циклу. Тут ми маємо два стани після закінчення місяця t: поломка автомобіля з вірогідністю pt і її відсутність з вірогідністю 1-pt. Отже, очікуване число поломок після закінчення місяця t рівне кількості автомашин в парку, помноженому на pt, тобто 20pt. Використовуючи цей результат, підрахуємо очікуване загальне число автомобілів, що зламалися, впродовж перших N-1 місяців циклу у вигляді суми відповідних величин для кожного місяця окремо, тобто
![]()
Позначивши через ЄС(N) загальну очікувану вартість для циклу між профілактичними ремонтами,
маємо наступне.
![]() .
.
Задача вибору рішення компанією зводиться таким чином до визначення довжини циклу N, яка мінімізує загальні очікувані витрати за один місяць ECPM(N), тобто величину
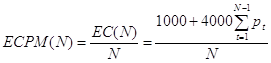 .
.
Мінімізацію функції ECPM(N) не можна виконати в явній формі. Натомість використовується наступна таблична форма знаходження рішення.
Таблиця 3.
| N | pi | | ECPM(N) | |
| 1 | 0.05 | 0 | 1000 | |
| Оптимальне N → | 2 | 0.07 | 0.05 | 600 |
| 3 | 0.1 | 0.12 | 493.33 | |
| 4 | 0.13 | 0.22 | 470 | |
| 5 | 0.18 | 0.35 | 480 | |
| 6 | 0.23 | 0.53 | 520 |
Обчислення показують, що ECPM(N) досягає свого мінімуму при N-4. Отже, профілактичний ремонт автомобілів потрібно виконувати кожного четвертого місяця.
2.3 Інші критерії очікуваного значення
У цьому розділі розглядаються три модифікації критерію очікуваного значення. Перша полягає у визначенні апостеріорної вірогідності на основі експерименту над досліджуваною системою, друга - в корисності реальної вартості грошей, а третя модифікує критерій очікуваного значення таким чином, що він може бути використаний для ухвалення рішень при короткостроковому плануванні.
Апостеріорна вірогідність Байеса
Розподіли вірогідності, які використовуються при формулюванні критерію очікуваного значення, виходять, як правило, з накопиченої раніше інформації. В деяких випадках виявляється можливим модифікувати цю вірогідність за допомогою поточної і/або одержаної раніше інформації, яка звичайно ґрунтується на дослідженні вибіркових (або експериментальних) даних. Одержувану при цьому вірогідність називають апостеріорними (або Байесовськими), на відміну від апріорних, одержаних з початкової інформації. Наступний приклад показує, як розглянутий в розділі 2.1 критерій очікуваного значення можна модифікувати так, щоб скористатися новою інформацією, що міститься в апостеріорній вірогідності.
Приклад 3.
У прикладі 1 апріорна вірогідність 0.6 і 0.4 підвищення і пониження котирувань акцій на біржі була визначена з наявних публікацій фінансового характеру. Припустимо, замість того щоб повністю покладатися на ці публікації, ви вирішили провести особисте дослідження шляхом консультацій з другом, який добре розбирається в питаннях, що стосуються фондової біржі. Друг виказує загальну думку "за" або "проти" інвестицій. Ця думка надалі визначається кількісно таким чином. При підвищенні котирувань його думка з 90%-ний вірогідністю буде "за", при зниженні котирувань вірогідність його думки "за" зменшиться до 50%. Яким чином можна отримати користь з цієї додаткової інформації?
Думка друга фактично представляє умовну вірогідність "за-проти" при заданих станах природи у вигляді підвищення і пониження котирувань. Введемо наступні позначення:
v1 - думка «за»,
v2 - думка «проти»,
m1 - підвищення котирувань,
m2 - пониження котирувань.
Думку друга можна записати у вигляді співвідношень вірогідності таким чином.
![]()
![]()
За допомогою цієї додаткової інформації задачу вибору рішення можна сформулювати таким чином.
1. Якщо думка друга "за", акції якої компанії слід купувати - А або б?
2. Якщо думка друга "проти", то, знову-таки, - акції якої компанії слід купувати - А або В?
Таблиця 4.
| Альтернативне рішення | Прибуток від інвестиції за рік | |||
| "за" | "проти" | |||
| Підвищенні котирувань | Пониженні котирувань | Підвищенні котирувань | Пониженні котирувань | |
| Акції компанії А | $5000, P=0.73 | $-2000, P=0.27 | $5000, P=0.231 | $-2000, P=0.769 |
| Акції компанії В | $1500, P=0.73 | $500, P=0.27 | $1500, P=0.231 | $500, P=0.769 |
Для оцінки різних альтернатив, показаних в таблиці 4, необхідно обчислити апостеріорну вірогідність P{mi|vj}. Ця апостеріорна вірогідність обчислюється з урахуванням додаткової інформації, що міститься в рекомендаціях друга, за допомогою наступних дій.
Крок 1. Умовну вірогідність P{vj|mi} для даної задачі запишемо таким чином.
| v1 | v2 | |
| m1 | 0.9 | 0.1 |
| m2 | 0.5 | 0.5 |
P{vj|mi}=
Крок 2. Обчислюємо вірогідність сумісної появи подій
![]() для всіх i та j.
для всіх i та j.
При заданій апріорній вірогідності P{m1}=0.6 і Р{m2}=0.4 вірогідності сумісної появи подій визначаються множенням першого і другого рядків таблиці, одержаної на кроці 1, на 0.6 і 0.4 відповідно. В результаті маємо наступне.
| v1 | v2 | |
| m1 | 0.54 | 0.06 |
| m2 | 0.2 | 0.2 |
P{vj|mi}=
Сума всіх елементів цієї таблиці рівна 1.
Крок 3. Обчислюємо абсолютну вірогідність.
![]() для всіх j.
для всіх j.
Ця вірогідність виходить шляхом підсумовування елементів відповідних стовпців таблиці, одержаної на кроці 2. У результаті маємо наступне.
| P{v1} | P{v2} |
| 0.74 | 0.26 |
Крок 4. Визначаємо шукану апостеріорну вірогідність по формулі
![]()
Ця вірогідність обчислюється в результаті розподілу кожного стовпця таблиці, одержаної на кроці 2, на елемент відповідного стовпця таблиці, обчисленої на кроці 3, що приводить до наступних результатів (закругленим до трьох десяткових знаків).
| v1 | v2 | |
| m1 | 0.73 | 0.231 |
| m2 | 0.27 | 0.769 |
P{vj|mi}=
Це та вірогідність, яка показана в таблиці 4. Вони відрізняються від початкової апріорної вірогідності
P{m1}=0.6 і P{m2}=0.4.
Тепер можна оцінити альтернативні рішення, засновані на очікуваних платежах.
Думка "за"
Дохід від акцій компанії А = 5000х0.73+(-2000) х0.270=$3110.
Дохід від акцій компанії В = 1500х0.73+500х0.270=$1230.
Рішення. Інвестувати в акції компанії А.
Думка "проти"
Дохід від акцій компанії А = 5000х0.231+(-2000) х0.769=-$383.
Дохід від акцій компанії В = 1500х0.231+500х0.769=$731.
Рішення. Інвестувати в акції компанії В.
Функції корисності.
У попередніх прикладах критерій очікуваного значення застосовувався лише в тих ситуаціях, де платежі виражалися у вигляді реальних грошей. Є численні випадки, коли при аналізі слід використовувати швидше корисність, ніж реальну величину платежів. Для демонстрації цього припустимо, що є шанс 50 на 50, що інвестиція в 20 000 доларів або принесе прибуток в 40 000 доларів, або буде повністю втрачена. Відповідний очікуваний прибуток рівний 40000 х 0.5 - 20000 х 0.5 = 10000 доларів. Хоча тут очікується прибуток у вигляді чистого доходу, різні люди можуть по-різному інтерпретувати одержаний результат. Інвестор, який йде на ризик, може зробити інвестицію, щоб з вірогідністю 50% одержати прибуток в 40 000 доларів. Навпаки, обережний інвестор може не висловити бажання ризикувати втратою 20 000 доларів. З цієї точки зору очевидно, що різні індивідууми проявляють різне відношення до ризику, тобто вони проявляють різну корисність по відношенню до ризику.
Визначення корисності є суб'єктивним. Воно залежить від нашого відношення до ризику. У цьому розділі ми представляємо систематизовану процедуру числової оцінки відношення до ризику особи, що ухвалює рішення. Кінцевим результатом є функція корисності, яка займає місце реальних грошей. У прикладі, приведеному вище, якнайкращий платіж рівний $40 000, а якнайгірший - -$20 000. Отже, ми встановлюємо довільну, але логічну шкалу корисності U, що змінюється від 0 до 100, де 0 відповідає корисності -$20 000, а 100 - $40000. тобто U(-20000)= 0 і U(40000)= 100. Далі визначаємо корисність в крапках між $-20000 і $40000 для визначення загального виду функції корисності. Якщо відношення особи, що ухвалює рішення, неупереджене до ризику, то результуюча функція корисності є прямою лінією, що сполучає крапки (0, -$20000) і (100, $40000). В цьому випадку як реальні гроші, так і їх корисність дають співпадаючі рішення. У реальніших ситуаціях функція корисності може приймати вигляд, що відображає відношення до ризику особи, що ухвалює рішення. Візьмемо для прикладу 3-х індивідуумів X, У і Z. Індивідуум X не розташований до ризику (обережний), оскільки проявляє велику чутливість до втрати, ніж до прибутку. Індивідуум Z - протилежність в цьому відношенні Індивідуума X: він налаштований на ризик. Це витікає з того, що для індивідуума X при зміні в 10000 доларів управо і ліворуч від крапки, відповідної 0 доларів, збільшення прибутку змінює корисність на величину ab, яка менше зміни корисності bc, обумовленої втратами такої ж величини, тобто ab < bc. В той же час такі ж зміни в ±10000 доларів, що відносяться до індивідуума Z, знаходять протилежну поведінку; тут de > ef. Далі, індивідуум У є нейтральним до ризику, оскільки згадані зміни породжують однакові зміни корисності. У загальному випадку індивідуум може бути як не розташований до ризику, так і налаштований на ризик, залежно від суми ризику. В цьому випадку відповідна крива корисності матиме вид подовженої букви S.
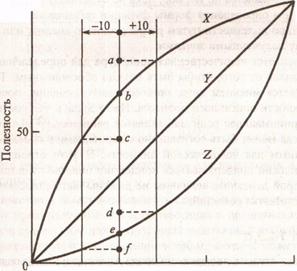
Криві корисності визначені за допомогою кількісного показника, що характеризує відношення до ризику особи, що ухвалює рішення, для різних значень рівня реальних грошей в межах встановленого інтервалу. Так в розглянутому прикладі встановленим інтервалом є (- $20000, $40000), відповідна корисність змінюється в інтервалі (0, 100). Необхідно визначити корисність, відповідну таким проміжним значенням, наприклад, як -$10 000, $0, $10 000, $20 000 або $30 000. Відповідна процедура побудови функції корисності починається з того, що організовується лотерея для визначення суми реальних грошей x, для якої очікуване значення корисності буде обчислене по наступній формулі.
![]() , 0≤p≤1.
, 0≤p≤1.
Для визначення значення U(x) просять особу, що ухвалює рішення, повідомити свою перевагу між гарантованою наявною сумою х і можливістю зіграти в лотерею, в якій з вірогідністю p реалізується програш в сумі $20000 і з вірогідністю 1-p має місце виграш в $40000. При цьому під перевагою розуміється вибір значення "нейтральної" вірогідності p, при якому з погляду особи, що ухвалює рішення, можливості зіграти в лотерею і одержати гарантовану суму х є однаково привабливими. Наприклад, якщо х=$20000, особа, що ухвалює рішення, може заявити, що гарантовані 20000 доларів готівкою і лотерея однаково привабливі при р = 0.8. В цьому випадку обчислюється корисність для х = $20000 по наступній формулі.
U(20000) =100-100×0.8=20.
Ця процедура продовжується до тих пір, поки не буде одержана достатня кількість крапок (х, U(x)) для визначення форми функції корисності. Потім можна визначити шукану функцію корисності шляхом регресійного аналізу або просто лінійній інтерполяції між одержаними крапками.
Хоча тут застосовується кількісна процедура для визначення функції корисності, сам підхід далекий від того, щоб бути науково обґрунтованим. Те, що процедура повністю визначається думкою особи, що ухвалює рішення, породжує сумніви щодо надійності описаного процесу. Процедура, зокрема, неявно припускає, що особа, що ухвалює рішення, є раціонально мислячим - вимога, яка не завжди може бути узгоджене з варіаціями в поведінці і настрої, що є типовим для людської особи. В цьому відношенні особа, що ухвалює рішення, повинна дотримуватися концепції корисності в широкому значенні, відповідно до якої грошові величини не повинні бути єдиним вирішальним чинником в теорії ухвалення решений.3. Антикризове управління як основа управління ризиками.
Похожие работы
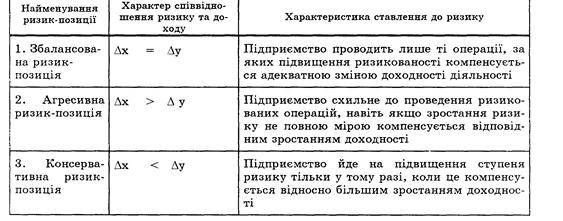
... обґрунтованою. Але при цьому необхідно звернути увагу на поглиблення рівня спеціалізації за рахунок реконструкції, модернізації, придбання нових засобів виробництва. 3. Прийняття управлінських рішень в умовах ризику 3.1 Ризик-позиція підприємства та її характеристика Розглядаючи конкретну господарську операцію підприємства та оцінюючи доцільність та ефективність її проведення, слід порі ...
... інформацією і відрегулювати відповідні відносини підпорядкування між учасниками. Менеджер повинний виявити занепокоєння про конфлікт інтересів і прийняття рішення його виконавцями як зразка поводження. Наступний етап - це вбудовування в рішення механізму одержання інформації про хід виконання рішення. Тобто повинна здійснюватися функція контролю - установлення стандартів і вимір показників ...
... приведені витрати: С1+ЕнК1=тт, де С1 — собівартість робіт; Ен — нормативний коефіцієнт ефективності капітальних вкладень; К1 — капітальні вкладення для кожного варіанта. Ефективність i якість управлінських рішень можна оцінювати також за такими показниками: 1) економічною ефективністю рішень — як відношення результативності реалізації рішень до витрат на досягнення поставлених цілей; 2) коеф ...
... які корективи необхідно застосувати? · хто винен у тому, що досягнуті показники значно менші від запланованих, або хто (чи що) найбільше сприяє успішній роботі? Управлінські рішення можна систематизувати за ознаками: 1. За сферою охоплення чи масштабом можливих наслідків: · загальні (прямо чи опосередковано стосуються усієї організації · часткові (торкаються лише деяких ...




0 комментариев