Предпосылки методологии математического развития дошкольников
Программные требования к методике преподавания математики дошкольникам в современных ДОУ
Игра - как метод математического развития
Методика обучения счету с помощью сюжетно-дидактических игр
Методика обучения счету в старшей группе с помощью дидактической игры«Цирк»
Навигация
Предпосылки методологии математического развития дошкольников
Использование игровых приемов при обучении дошкольников счету
70789
знаков
2
таблицы
0
изображений
1.1 Предпосылки методологии математического развития дошкольников
Если в два одинаковых прозрачных стакана налить одинаковое количество слегка подкрашенной воды (для подкрашивания можно использовать несколько кристалликов марганцовки), а затем, показывая на стаканы, спросить у ребенка, в каком из них воды больше, а в каком - меньше? Практически все дети уверенно ответят, что воды в стаканах одинаковое количество. Затем, можно взять третий стакан, более узкий, и в присутствии ребенка перелить в него воду из первого стакана. Теперь снова спросить, в каком стакане, во втором или третьем, воды больше. Пусть вас не удивляет, если ребенок без колебаний заявит, что в третьем стакане воды больше. Все попытки переубедить ребенка ни к чему не приведут. В лучшем случае он сделает вид, что с вами согласился. Однако внимательное наблюдение покажет, что внутреннее его мнение осталось прежним. Почему это происходит? Разве ребенку непонятно, что при переливании осталась та же самая вода и больше ее не добавляли?
Эта задача - только одна из бесчисленной серии задач, которые предлагались детям в экспериментах известным швейцарским психологом Жаном Пиаже. В признание его заслуг эти задачи в научной литературе стали называться «задачами Пиаже», а выступающие в них явления - «феноменами Пиаже».[8, с.13]
Данный опыт можно повторить на самом разном материале и самыми разными способами, но, если одна из величин меняет свою форму так, что окажется в каком-то отношении явно больше или меньше другой, ребенок утверждает, что и величины стали больше или меньше.
Пиаже этот результат объясняет тем, что у ребенка еще отсутствует понимание «принципа сохранения количества». Ребенок думает, что количество вещества изменилось, если явно изменилось одно из его измерений. Если его спросить: «Почему?», то он, в случае с водой, отвечает: «Потому, что ее перелили».
Данные эксперименты требуют проведения целой серии занятий, которые ориентируют ребенка на количественную сторону объектов, создавая тем самым предпосылки для формирования у него потребности в счете.
Таким образом, математическое развитие - значимый компонент формирования «картины мира» ребенка. Одна из важных задач воспитателей и родителей – развить у ребенка интерес к математике в дошкольном возрасте. Приобщение к этому предмету в игровой и занимательной форме помогает ребенку в дальнейшем быстрее и легче усваивать школьную программу.
Особую остроту этой проблемы подчеркивал Л.С. Выготский, характеризуя возникающий в дошкольном возрасте тип обучения как промежуточный между спонтанным, свойственным ребенку раннего возраста, и реактивным, присущим школьному возрасту[19,103]. Ребенок в дошкольном возрасте уже может обучаться по программе, задаваемой взрослым, однако лишь в силу того, как программа взрослых становится его собственной программой, сливается с естественным ходом развития ребенка. Этот тип обучения Л.С.Выготский называл спонтанно-реактивным. [19,103]
И если для воспитанника цель – в самой игре, то для взрослого, организующего игру, есть и другая цель – развитие детей, усвоение ими определенных знаний, формирование умений, выработка тех или иных качеств личности. Характер этого противоречия и определяет воспитательную ценность игры: если достижение дидактической цели будет осуществимо в игре как деятельности, заключающей цель в самой себе, то воспитательная ее ценность будет более значимой.
По словам Л.С. Выготского, научные понятия не усваиваются и не заучиваются ребенком, не берутся памятью, а возникают и складываются с помощью величайшего напряжений всей активности его собственной мысли [18,51]. При этом математика может и должна играть особую роль в гуманизации образования, в его ориентации на воспитание и развитие детской личности. Особая роль математики – в умственном воспитании, в развитии интеллекта. Знания необходимы ребенку не ради знания, а как важная составляющая личности, включающая умственное, нравственное, эмоциональное (эстетическое) и физическое воспитание.
Обучению дошкольников основам математики отводиться важное место. Это вызвано целым рядом причин: началом школьного обучения с шести лет, обилием информации, получаемой ребенком, повышенное внимание к компьютеризации, желанием сделать процесс обучения более интенсивным.
Крутецкий В.А. выделил девять компонентов математических способностей [21,56]:
1. Способность к формализации математического материала, к отделению формы от содержания абстрагированного, от конкретных количественных отношений и пространственных форм и оперированию формальными структурами, структурами отношений и связей;
2. Способность обобщать математический материал, вычленять главное, отвлекаясь от несущественного, видеть общее во внешне разном;
3. Способность к последовательному, правильно расчлененному логическому рассуждению, связанному с потребностью в доказательстве, обосновании, выводах;
4. Способность сокращать процесс рассуждения, мыслить развернутыми структурами, мыслить свернутыми структурами;
5. Способность сокращать процесс рассуждения, мыслить развернутыми структурами, мыслить свернутыми структурами;
6. Способность к обратимости мыслительного процесса (к переходу с прямого на обратный ход мысли);
7. Гибкость мышления, способность к переключению от одной умственной операции к другой. Свобода от сковывающего влияния шаблонов и трафаретов;
8. Математическая память – память на обобщенные формализованные структуры, логические схемы;
9. Способность к пространственным представлениям.
Я.А.Коменский в своей «Великой дидактике» указывал, что в первые 6 лет жизни ребенка должна быть заложена основа для многих последующих занятий. Определяя содержание этой основы, Я.А.Коменский отметил, что в период так называемой «Материнской школы» с ребенком необходимо пройти «первые шаги хронологии».
По мнению Ф. Фребеля первые математические представления ребенок должен усвоить в процессе деятельности, в играх и занятиях с дидактическим материалом.
В педагогических системах И.Г. Песталоцци, Ф. Фребеля, М. Монтессори и др. обосновывается необходимость математического развития детей, а в связи с этим выдвигаются идеи о совершенствовании методов их обучения. [23,114]:
Основоположником теории начального обучения считают И.Г. Песталоцци, резко критиковавшего существовавшие тогда догматические методы обучения. Он предлагал обучать детей счёту на основе понимания действий с числами, а не простого запоминания результатов вычислений. Суть разрабатываемой И.Г.Песталоцци методики заключалась в переходе от простых элементов счёта к более сложным. Особое значение придавалось наглядным методам, облегчающим усвоение детьми чисел.
Ф. Фребель и М. Монтессори большое внимание уделяли наглядным и практическим методам. Разработанные специально пособия («дары» Ф.Фребеля и дидактические наборы М. Монтессори) обеспечивали усвоение достаточно осознанных знаний у детей. В методике Ф. Фребеля в качестве основного метода использовалась игра, в которой ребёнок получал достаточную свободу.
По мнению Ф. Фребеля и М. Монтессори, свобода ребёнка должна быть активной и опираться на самостоятельность. Роль педагога в таком случае сводилась к созданию благоприятных условий.[12, с. 53]
Теория и практика обучения накопила определённый опыт использования разных методов обучения в работе с детьми дошкольного возраста. При этом классификация методов используется с опорой на средства обучения. В период становления общественного дошкольного воспитания на развитие методики формирования элементарных математических представлений оказали влияние методы обучения математике в начальной школе. В практику работы детских садов проникли монографический метод А.В. Грубе и вычислительный метод (метод изучения действий). Работая с дошкольниками, Е.И. Тихеева внесла много нового в разработку методов обучения детей. Составленные ею игры-занятия сочетали в себе слово, действие и наглядность. По её мнению, дети до 7 лет должны учиться считать в процессе игры и повседневной жизни. Игру как метод обучения Е.И. Тихеева предлагала вводить по мере того, как то или другое числовое представление уже «извлечено детьми из самой жизни».
В 30-е гг. идею использования игр в обучении дошкольников счёту обосновывала Ф.Н. Блехер.
Существенный вклад в разработку дидактических игр и включения их в систему обучения дошкольников началам математики внесли Т.В. Васильева, Т.А. Мусейибова, А.И. Сорокина, Л.И. Сысуева, Е.И. Удальцова и др. Начиная с 50-х гг. в обучении детей всё чаще используют практические методы (А.М. Леушина). Она рассматривала практические методы в системе других (словесных и наглядных)методов. Именно с практических действий с предметными множествами начинается знакомство детей с элементарной математикой. Это было доказано в исследованиях как А.М. Леушиной, так и её учеников. [25, 95-99]
Похожие работы
... были подобраны и систематизированы дидактические игры, которые могут быть использованы в логопедической работе с детьми с общим недоразвитием речи 3 уровня по формированию у них грамматического строя речи. 2.2. Педагогическая технология коррекции лексико-грамматических нарушений у детей. Второй этап практического исследования, формирующий, был направлен на организацию коррекционной работы ...
... представлений детей дошкольного возраста, а это подтверждает нашу гипотезу. ЗАКЛЮЧЕНИЕ Целью исследования было изучение проблемы использования игровых приёмов при формировании элементарных математических представлений у дошкольников. Для ее достижения мы проанализировали психолого-педагогическую литературу по проблеме исследования, рассмотрели и проанализировали игровой метод в ...
... важен учет психологических особенностей ребенка. Одни дети активны и самостоятельны, другие напротив, вялы, малоподвижны. В качестве рекомендаций по использованию игровых приемов в коррекции двигательных нарушений у детей старшего дошкольного возраста с ДЦП необходимо отметить: 1) Необходимо учитывать темп, в котором ведется подвижная игра. Его следует с особой тщательностью регулировать ...
... наблюдений дети знакомятся с жизнью растений и животных, условиями их содержания, приобретают полезные трудовые навыки. Нужно учить детей самостоятельно следить за состоянием комнатных растений (определять необходимость полива), за их чистотой. Дошкольники овладевают такими навыками ухода за растениями, как рыхление, опрыскивание, очистка разными способами листьев от пыли. Они постепенно начинают ...
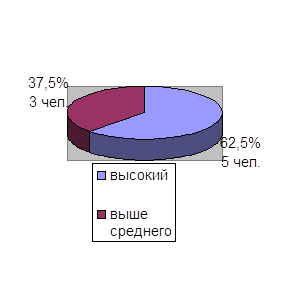
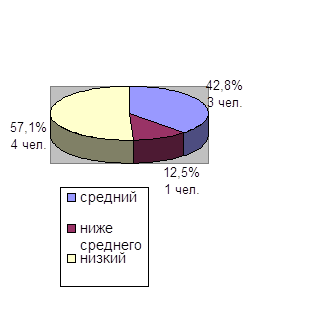
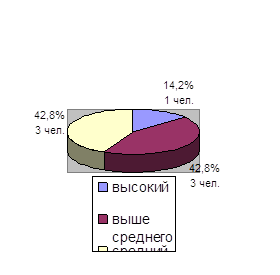
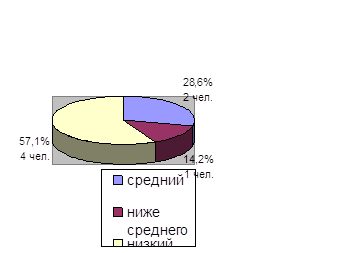
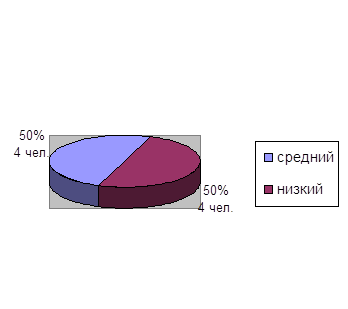
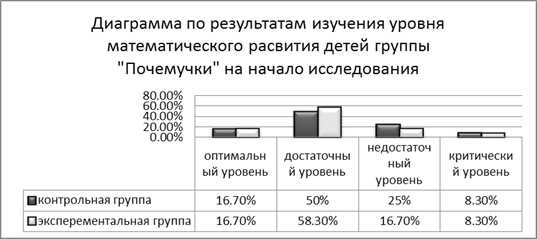
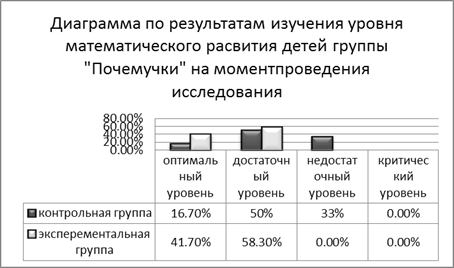
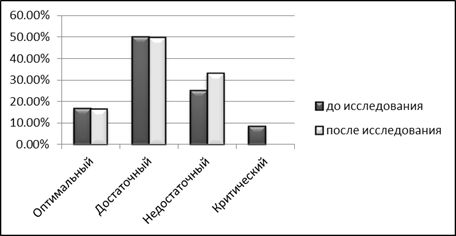
0 комментариев