Навигация
Создание условий для формирования элементарных математических представлений в разновозрастных группах
1.2 Создание условий для формирования элементарных математических представлений в разновозрастных группах
Успешное обучение детей в начальной школе зависит от уровня развития мышления ребёнка, умения обобщать и систематизировать свои знания, творчески решать различные проблемы. Развитое математическое мышление не только помогает ребёнку ориентироваться и уверенно себя чувствовать в окружающем его современном мире, но и способствует его общему умственному развитию. Отсюда вытекает основное требование к форме организации обучения и воспитания – сделать занятия по формированию элементарных математических представлений максимально эффективными для того, чтобы на каждом возрастном этапе обеспечить усвоение ребёнком максимальным доступным ему объёмом знаний и стимулировать поступательное интеллектуальное развитие.
Работу по развитию у детей элементарных математических представлений воспитатель организует на занятиях и вне занятий 2 – 3 раза в неделю. Занятия состоит из нескольких частей, объединенных одной темой. Продолжительность и интенсивность занятий на протяжении всего года увеличивается постепенно. В структуру каждого занятия предусмотрен перерыв для снятия умственного и физического напряжения продолжительностью 1-3 минуты. Это может быть динамическое упражнение с речевым сопровождением или "пальчиковая гимнастика", упражнения для глаз или упражнение на релаксацию. На каждом занятии дети выполняют различные виды деятельности с целью закрепления у математических знаний [22, c. 5].
На занятиях по математике воспитатели используют методы (словесный, наглядный, игровой) и приемы (рассказ, беседа, описание, указание и объяснение, вопросы детям, ответы детей, образец, показ реальных предметов, картин, действия с числовыми карточками, цифрами, дидактические игры и упражнения, подвижные игры и др.) [22, c. 6].
Комплексное использование всех методов и приемов, форм обучения поможет решить одну из главных задач – осуществить математическую подготовку дошкольников и вывести развитие их мышление на уровень, достаточный для успешного усвоения математики в школе. При организации и проведении занятий по математике необходимо всегда помнить о возрасте детей и индивидуальных особенностях каждого ребенка. Поэтому необходимо более детально рассмотреть каждую возрастную группу и соотнести ее с методами и приемами, которые целесообразно будет использовать при обучении математике [18, c. 6].
Методы и приёмы обучения в младшей группе
В младшей группе начинают специальную работу по формированию элементарных математических представлений, закладывают основы математического развития детей [18, c. 7].
Занятия по развитию математических представлений детей проводится с сентября месяца в определенный день недели. Продолжительность занятия – 12 – 15 минут. Новые знания ребенок усваивает на основе непосредственного восприятия, когда следит за действиями педагога, слушает его пояснения и указания и сам действует с дидактическим материалом.
Внимание у детей 3 – 4 лет непроизвольное, неустойчивое, способность запоминать характеризуется непреднамеренностью. Поэтому на занятиях широко используются игровые приемы и дидактические игры. Они организуются так, чтобы по возможности в действии одновременно участвовали все дети и им не приходилось ждать своей очереди. Проводятся игры, связанные с активными движениями: ходьбой и бегом. Однако, используя игровые приемы, педагог не допускает, чтобы они отвлекали детей от главного (пусть еще и элементарной, но математической работы). Когда впервые выделяют какое-то свойство и важно сосредоточить на нем внимание детей, игровые моменты могут и отсутствовать [17, c. 9].
Большое значение имеет использование привлекательных для детей наглядных пособий. В каждом пособии ярко подчеркивается именно тот признак, на который должно быть направленно внимание малышей, и нивелируются остальные.
Выяснение математических свойств проводят на основе сравнения предметов, характеризующихся либо сходными, либо противоположными свойствами. Используются предметы, у которых познаваемое свойство ярко выражено, которые знакомы детям, без лишних деталей, различаются не более чем 1—2 признаками. Точности восприятия способствуют движения (жесты рукой), обведение рукой модели геометрической фигуры помогает детям точнее воспринять ее форму, а проведение рукой вдоль, скажем, шарфика, ленточки — установить соотношение предметов именно по данному признаку.
Детей приучают последовательно выделять и сравнивать однородные свойства вещей. Сравнение проводится на основе практических способов сопоставления: наложения или приложения [10, c. 25].
Большое значение придается работе детей с дидактическим материалом. Малыши уже способны выполнять довольно сложные действия в определенной последовательности. Однако, если ребенок не справляется с заданием, работает непроизводительно, он быстро теряет к нему интерес, утомляется и отвлекается от работы. Учитывая это, педагог дает детям образец каждого нового способа действия. Стремясь предупредить возможные ошибки, он показывает все приемы работы и детально разъясняет последовательность действий. При этом объяснения должны быть предельно четкими, ясными, конкретными, даваться в темпе, доступном восприятию маленького ребенка. Если педагог говорит торопливо, то дети перестают его понимать и отвлекаются. Наиболее сложные способы действия педагог демонстрирует 2—3 раза, обращая внимание малышей каждый раз на новые детали. Только многократный показ и называние одних и тех же способов действий в разных ситуациях при смене наглядного материала позволяют детям их усвоить. Когда дети усвоят способ действия, то его показ становится ненужным. Теперь им можно предложить выполнить задание только по словесной инструкции [5, c. 57].
Пространственные и количественные отношения могут быть отражены при помощи слов. Каждый новый способ действия, усваиваемый детьми, каждое вновь выделенное свойство закрепляются в точном слове. Новое слово педагог проговаривает не спеша, выделяя его интонацией. Все дети вместе (хором) его повторяют.
Наиболее сложным для малышей является отражение в речи математических связей и отношений, так как здесь требуется умение строить не только простые, но и сложные предложения. Воспитатель дает образец ответа. Если ребенок затрудняется, педагог может начать фразу-ответ, а ребенок ее закончит. Вначале приходится задавать детям вспомогательные вопросы, а затем просить их рассказать сразу обо всем.
Для осознания детьми способа действия им предлагают в ходе работы сказать, что и как они делают, а когда действие уже освоено, перед началом работы высказать предположение, что и как надо сделать. Устанавливаются связи между свойствами вещей и действиями, с помощью которых они выявляются. При этом педагог не допускает употребления слов, смысл которых не понятен детям [23, c. 91].
Методы и приёмы обучения в средней группе
В средней группе занятия по развитию элементарных математических
представлений проводятся еженедельно, в определенный день недели. Продолжительность занятия – 20 минут. На каждом занятии идет работа одновременно по новой теме и повторению пройденного. С первых занятий перед детьми данной группы ставят познавательные задачи, которые придают их действиям нацеленный характер [18, c. 48].
Внимание четырехлетних детей, как и трехлетних, еще не устойчиво. Для прочного усвоения знаний их необходимо заинтересовать работой. Непринужденный разговор с детьми, который ведется в неторопливом темпе, привлекательность наглядных пособий, широкое использование игровых упражнений и дидактических игр – все это создает у детей хороший эмоциональный настрой. Используются игры, в которых игровое действие является в то же время элементарным математическим действием.
На занятиях по математике используют наглядно-действенные приемы обучения: показ педагогом образцов и способов действий, выполнение детьми практических заданий, включающих элементарную математическую деятельность.
На пятом году у детей интенсивно развивается способность к исследовательским действиям. В связи с этим ребят побуждают к более или менее самостоятельному выявлению свойств и отношений математических объектов. Педагог ставит перед детьми вопросы, требующие поиска. Он подсказывает, а если требуется — показывает, что нужно сделать, чтобы найти на них ответ.
Дети приобретают знания опытным путем, отражая в речи то, что непосредственно наблюдали. Тем самым удается избежать отрыва словесной формы высказывания от выраженного в нем содержания, т. е. устранить формальное усвоение знаний. Это особенно важно! Дети данного возраста легко запоминают слова и выражения, подчас не соотнося их с конкретными предметами, их свойствами [18, c. 49].
Место и характер использования наглядных (образец, показ) и словесных (указания, пояснения, вопросы и др.) приемов обучения определяются уровнем усвоения детьми изучаемого материала. Когда дети знакомятся с новыми видами деятельности (счетом, отсчетом, сопоставлением предметов по размерам), необходимы полный, развернутый показ и объяснение всех приемов действий, их характера и последовательности, детальное и последовательное рассматривание образца. Указания побуждают детей следить за действиями педагога или вызванного к его столу ребенка, знакомят их с точным словесным обозначением данных действий. Пояснения должны отличаться краткостью и четкостью. Недопустимо употребление непонятных детям слов и выражений.
В ходе объяснения нового детей привлекают к совместным с педагогом действиям, к выполнению отдельных действий. Новые знания лишь постепенно приобретают для детей данного возраста свой обобщенный смысл.
В средней группе, как и в младшей, необходим неоднократный показ новых для детей действий, при этом меняются наглядные пособия, незначительно варьируются задания, приемы работы. Так обеспечивается проявление детьми активности и самостоятельности в усвоении новых способов действий. Чем разнообразнее работа детей с наглядными пособиями, тем более сознательно они усваивают знания. Педагог ставит вопросы так, чтобы новые знания нашли отражение в точном слове. Детей постоянно учат пояснять свои действия, рассказывать о том, что и как они делали, что получилось в результате. Воспитатель терпеливо выслушивает ответы детей, не спешит с подсказкой, не договаривает за них. При необходимости дает образец ответа, ставит дополнительные вопросы, в отдельных случаях начинает фразу, а ребенок ее заканчивает. Исправляя ошибки в речи, педагог предлагает повторить слова, выражения, побуждает детей опираться на наглядный материал. По мере усвоения соответствующего словаря, раскрытия смыслового значения слов дети перестают нуждаться в полном, развернутом показе [27, c. 65].
На последующих занятиях они действуют в основном по словесной инструкции. Педагог показывает лишь отдельные приемы. Посредством ответов на вопросы ребенок повторяет инструкцию, например, говорит, какого размера полоску надо положить сначала, какую после. Дети учатся связно рассказывать о выполненном задании. В дальнейшем они действуют на основе лишь словесных указаний. Однако, если дети затрудняются, педагог прибегает и к образцу, и к показу, и к дополнительным вопросам. Все ошибки исправляются в процессе действия с дидактическим материалом.
Постепенно увеличивают объем заданий, они начинают состоять из 2—3 звеньев.
Методы и приёмы обучения в старшей группе
В старшей группе продолжительность занятия изменяется незначительно по сравнению со средней (с 20 – 25 минут), но заметно увеличивается объем знаний и темп работы [17, c. 82].
Наглядные, словесные и практические методы и приемы обучения на занятиях по математике в старшей группе в основном используются в комплексе. Пятилетние дети способны понять познавательную задачу, поставленную педагогом, и действовать в соответствии с его указанием. Постановка задачи позволяет возбудить их познавательную активность. Создаются такие ситуации, когда имеющихся знаний оказывается недостаточно для того, чтобы найти ответ на поставленный вопрос, и возникает потребность узнать что-то новое, научиться новому.
Побудительным мотивом к поиску являются предложения решить какую-либо игровую или практическую задачу.
Организуя самостоятельную работу детей с раздаточным материалом, педагог также ставит перед ними задачи (проверить, научиться, узнать новое и т. п.) [18, c. 92].
Закрепление и уточнение знаний, способов действий в ряде случаев осуществляется предложением детям задач, в содержании которых отражаются близкие, понятные им ситуации. Заинтересованность детей в решении таких задач обеспечивает активную работу мысли, прочное усвоение знаний.
Математические представления «равно», «не равно», «больше — меньше», «целое и часть» и др. формируются на основе сравнения. Дети 5 лет уже могут под руководством педагога последовательно рассматривать предметы, выделять и сопоставлять их однородные признаки. На основе сравнения они выявляют существенные отношения, например отношения равенства и неравенства, последовательности, целого и части и др., делают простейшие умозаключения.
Развитию операций умственной деятельности (анализ, синтез, сравнение, обобщение) в старшей группе уделяют большое внимание. Все эти операции дети выполняют с опорой на наглядность. Так в старшей группе детям предъявляются предметы, имеющие уже 2—3 признака различия.
Детей сначала учат производить сравнение предметов попарно, а затем сопоставлять сразу несколько предметов. Одни и те же предметы они располагают в ряд или группируют то по одному, то по другому признаку. Наконец, они осуществляют сравнение в конфликтной ситуации, когда существенные признаки для решения данной задачи маскируются другими, внешне более ярко выраженными. Сравнение производится на основе непосредственных и опосредованных способов сопоставления и противопоставления (наложения, приложения, счета, «моделирования измерения»). В результате этих действий дети уравнивают количества объектов или нарушают их равенство, т. е. выполняют элементарные действия математического характера [2, c. 93].
Выделение и усвоение математических свойств, связей, отношений достигается выполнением разнообразных действий. Большое значение в обучении детей 5 лет по-прежнему имеет активное включение в работу разных анализаторов.
Рассматривание, анализ и сравнение объектов при решении задач одного типа производятся в определенной последовательности. Например, детей учат последовательному анализу и описанию узора, составленного из моделей геометрических фигур, и др. Постепенно они овладевают общим способом решения задач данной категории и сознательно им пользуются.
Так как осознание содержания задачи и способов ее решения детьми этого возраста осуществляется в ходе практических действий, ошибки, допускаемые детьми, всегда исправляются через действия с дидактическим материалом [16, c. 102].
В старшей группе расширяют виды наглядных пособий и несколько изменяют их характер. В качестве иллюстративного материала продолжают использовать игрушки, вещи. Но теперь большое место занимает работа с картинками, цветными и силуэтными изображениями предметов, причем рисунки предметов могут быть схематичными.
С середины учебного года вводятся простейшие схемы, например «числовые фигуры», «числовая лесенка», «схема пути» (картинки, на которых в определенной последовательности размещены изображения предметов).
Наглядной опорой начинают служить «заместители» реальных предметов. Отсутствующие в данный момент предметы педагог представляет моделями геометрических фигур. Опыт показывает, что дети легко принимают такую абстрактную наглядность. Наглядность активизирует детей и служит опорой произвольной памяти, поэтому в отдельных случаях моделируются явления, не имеющие наглядной формы. Например, дни недели условно обозначают разноцветными фишками. Это помогает детям установить порядковые отношения между днями недели и запомнить их последовательность.
В работе с детьми 5—6 лет повышается роль словесных приемов обучения. Указания и пояснения педагога направляют и планируют деятельность детей. Давая инструкцию, он учитывает, что дети знают и умеют делать, и показывает только новые приемы работы. Вопросы педагога в ходе объяснения стимулируют проявление детьми самостоятельности и сообразительности, побуждая их искать разные способы решения одной и той же задачи [18, c. 94].
Детей учат находить разные формулировки для характеристики одних и тех же математических связей и отношений. Существенное значение имеет отработка в речи новых способов действия. Поэтому в ходе работы с. раздаточным материалом педагог спрашивает то одного, то другого ребенка, что, как и почему он делает. Один ребенок может выполнять в это время задание у доски и пояснять свои действия. Сопровождение действия речью позволяет детям его осмыслить. После выполнения любого задания следует опрос. Дети отчитываются, что и как они делали и что получилось в результате.
По мере накопления умения выполнять те или иные действия ребенку можно предложить сначала высказать предположение, что и как надо сделать (построить ряд предметов, сгруппировать их и пр.), а потом выполнить практическое действие. Так учат детей планировать способы и порядок выполнения задания.
Усвоение правильных оборотов речи обеспечивается многократным их повторением в связи с выполнением разных вариантов заданий одного типа.
В старшей группе начинают использовать словесные игры и игровые упражнения, в основе которых лежат действия по представлению.
Усложнение и вариантность приемов работы, смена пособий и ситуаций стимулируют проявление детьми самостоятельности, активизируют их мышление. Для поддержания интереса к занятиям педагог постоянно вносит в них элементы игры (поиск, угадывание) и соревнования.
На основе всего вышесказанного, можно сделать следующий вывод: использование различных методов и приемов при формировании элементарных математических представлений зависит от возраста детей, уровня математического развития, индивидуальных особенностей каждого ребенка. А также следует отметить и такую особенность, что для более эффективного обучения детей математике необходимо интегрирование всех методов и приемов обучения детей дошкольного возраста.
Похожие работы
... и качественное улучшение системы математического развития дошкольников позволяет педагогам искать наиболее интересные формы работы, что способствует развитию элементарных математических представлений. 3. Дидактические игры дают большой заряд положительных эмоций, помогают детям закрепить и расширить знания по математике. ПРАКТИЧЕСКИЕ РЕКОМЕНДАЦИИ 1. Познание свойств детьми 4-5 лет ...
... . Игру как метод обучения Е.И. Тихеева предлагала вводить по мере того, как то или другое числовое представление уже «извлечено детьми из самой жизни». В 30-е гг. идею использования игр в обучении дошкольников счёту обосновывала Ф.Н. Блехер. Существенный вклад в разработку дидактических игр и включения их в систему обучения дошкольников началам математики внесли Т.В. Васильева, Т.А. Мусейибова, ...
... результатов эксперимента проводилось на основе результатов нулевого и промежуточного срезов. Эффективность экспериментального исследования мы определили в соответствии с динамикой развития математических представлений у старших дошкольников посредством информационных технологий. Выводы по главе II В результате проведенного эксперимента нами были решены и сделаны следующие результаты: 1. ...
... воззрений. Именно педагоги высокого класса способны внести в действие резервы главного воспитательного возраста - дошкольного. 1.4. Педагогические условия интеллектуального развития старшего дошкольника в процессе формирования первичных математических представлений Академик А.В.Запорожец писал, что оптимальные педагогические условия для реализации потенциальных возможностей маленького ребенка, ...
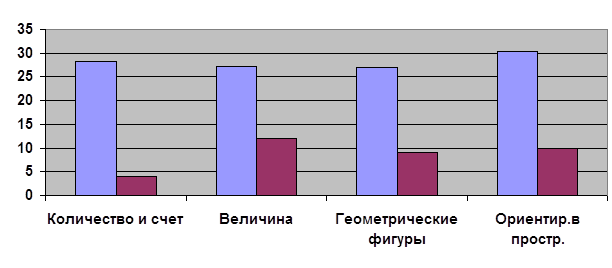
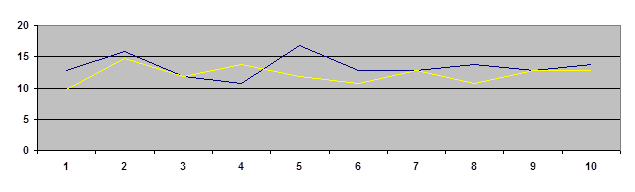

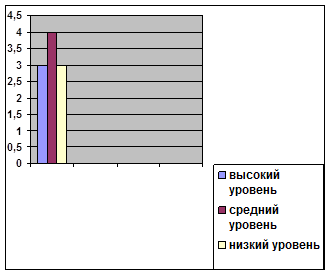
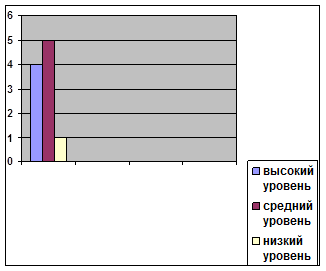


0 комментариев