Развивающая функция учебника способствует развитию мотивов учения, памяти, мышления, воображения, речи, способностей
Самоопределение к деятельности (организационный момент)
Особенности работы по учебнику математики
Логико-структурный анализ учебника математики М.И. Моро
Сравнительная характеристика учебников по математике для 2 класса Л.Г. Петерсон и М.И. Моро
Задания на развитие памяти и речи. Актуализация знаний
Навигация
Задания на развитие памяти и речи. Актуализация знаний
Использование учебников математики при изучении табличного умножения и деления на 2 и 3
68461
знак
2
таблицы
2
изображения
2.2 Задания на развитие памяти и речи. Актуализация знаний
- Повторите по порядку слова, которые я назову: слагаемое, слагаемое, сумма, уменьшаемое, вычитаемое, разность. (Дети пытаются воспроизвести порядок слов.)
- Компоненты каких действий назвали? (Сложение и вычитание.)
- С каким новым действием мы познакомились? (Умножение.)
- Назовите компоненты умножения. (Множитель, множитель, про изведение.)
- Что обозначает первый множитель? (Равные слагаемые в сумме.)
- Что обозначает второй множитель? (Число таких слагаемых.)
- 
Запишите определение умножения. (а + а + ... + а = а • n)
n раз
- Рассмотрите записи. Какое задание будете выполнять?
12+12+12+12+1233 + 33 + 33 + 33а + а + а
(Заменить сумму произведением.)
-Что получится? (В первом выражении 5 слагаемых, каждый из которых равен 12. поэтому оно равно 12 • 5. Аналогично - 33 • 4. а • 3)
- Назовите обратную операцию. (Заменить произведение суммой.)
-Замените произведение суммой в выражениях:
99 • 2, 8 • 4. b • 3. (99 + 99. 8 + 8 + 8 + 8, b + b + b.)
- На доске записаны равенства: 81+81 = 81 • 2 21 • 3 = 21+22 + 23
44 + 44 + 44 + 44 = 44 + 4 17 + 17 - 17 + 17 - 17 = 17 • 5
Учитель рядом с каждым равенством помещает картинки соответственно цыпленка, слоненка, лягушонка и мышонка.
- Зверюшки лесной школы выполняли задание. Правильно ли они его выполнили?
Дети устанавливают, что слоненок, лягушонок и мышонок ошиблись, объясняют, в чем их ошибки.
- Сравните выражения:
8 • 5...5 • 8 34 • 9...31 • 2
5 • 6...3 • 6 а• 3...а • 2 + а
(8 • 5 = 5 • 8. так как от перестановки слагаемых сумма не изменяется; 5 • 6 > 3 • 6, так как слева и справа по 6 слагаемых, но слева слагаемые больше: 34 • 9 > 31 • 2. так как слева слагаемых больше и сами слагаемые больше: а • 3 = а • 2 + а. так как слева и справа по 3 слагаемых, равных а.)
- Какое свойство умножения использовали в первом примере? (Переместительное.)
Физкультминутка.
Закрепление.
- Сегодня в гости к нам придет один герой, а как его зовут вы узнаете, расшифровав запись:
[Р] (18+2)-8 [О] (42 + 9) + 8
[А] 14-(4 + 3) [Н] 48 + 26-26
[Ф] 9 + (6 + 1) [Т] 15 + 23-15
| 16 | 59 | 12 | 23 | 12 | 7 | 48 |
У каждого ученика - карточка с заданием. Дети самостоятельно выполняют вычисления и расшифровывают запись:
| 16 | 59 | 12 | 23 | 12 | 7 | 48 |
| Ф | О | Р | Т | Р | А | Н |
- К кому же мы приглашены в гости? (К Фортрану.)
- Профессор Фортран - знаток компьютеров. Отправляемся к нему в гости.
- Нас встречает профессор Фортран со своими учениками. Его лучшая ученица - гусеница - приготовила для вас задание: «Я задумала число, вычла из него 7, прибавила 15, потом прибавила 4 и получила 45. Какое число я задумала?»
-7 +15 +4
- Обратные операции надо делать в обратном порядке:
45-4-15 + 7 =31.
- А сам профессор Фортран предложил нам поиграть в игру «Вычислительные машины».
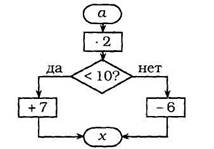
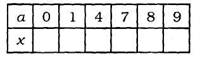
Таблица в тетрадях у учеников. Они самостоятельно выполняют вычисления и заполняют таблицу. Выигрывают первые 5 человек, которые справляются с заданием правильно.
Гусеница предложила решить еще несколько заданий на карточках для самостоятельного выполнения на отдельных листках. После его выполнения сдаем
1. Найди лишнее выражение:
5 * 4 4 * 5 4 * 6 – 4 4 * 2 + 4 * 3 5 * 3 + 4
2. Запиши числа в виде произведения с множителем 2 (двумя способами):
8 = 4*2 = 2*4 6 = * = *
12 = * = * 18 = * = *
16 = * = * 14 = * =*
10 = * = * 2 = * = *
3. Ластик стоит x руб. Сколько стоят 2 ластика? Составь выражение и найди его значение для x = 4, x = 9.
4. Реши уравнения:
х * 2 = 3 * у =15 18 : х = 3 12 : у = 4
х = у = х = у =
- Кто решил задания кладет их на край стола и после урока сдаем их.
Итог урока.
- Фортран говорит вам спасибо за хорошую работу на уроке. Ему очень понравилось у нас, и он сказал, что снова придет к вам с новыми заданиями.
Похожие работы
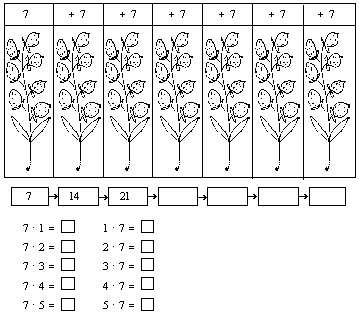
... в общем виде. Приведем систему заданий по различным разделам программы, построенную в соответствии с формированием диалектических приемов умственных действий и основными понятиями, включенными в программу математики для третьего класса. I. Табличные умножение и деление Приведем систему заданий при изучении табличного умножения и деления на примере изучения таблицы умножения и деления на 7. ...
... и суммы на число. Рассмотрение этих двух правил диктуется методическими соображениями. Глава II. Исследовательская работа по изучению формирования понятия свойств арифметических действий у младших школьников 2.1 Изучение арифметических действий и их свойств в различных системах обучения В программе Моро М.И. уделяется значительное внимание формированию у учащихся осознанных и прочных, ...
... уроки сказки, веселые задачи в стихах, математические загадки, сказочные задачи, математические сказки, задачи занимательного характера, головоломки, кроссворды и логические задачи способствуют активизации мыслительной деятельности учащихся на уроках математики, подтвердилась. Для себя лично я усвоила правило: "Не бери игру на урок, для того чтобы развлечься. Все на уроке должно быть логически ...
... 5 человек; низкий уровень мышления (6 баллов) – 4 человека. Далее переходим ко второму этапу эксперимента – формирующему. Описанию которого посвятим п.3.2. 3.2. ИСПОЛЬЗОВАНИЕ ПРОБЛЕМНЫХ СИТУАЦИЙ НА УРОКАХ МАТЕМАТИКИ В РАЗВИТИИ ТВОРЧЕСКОГО МЫШЛЕНИЯ УЧАЩИХСЯ В последнее время учителя начальных классов довольно часто при изучении математики создают на уроках проблемные ситуации. Однако чаще всего ...
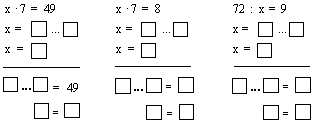
0 комментариев