Навигация
Виды упражнений, направленных на формирование представлений о функциональной зависимости у младших школьников
1.3 Виды упражнений, направленных на формирование представлений о функциональной зависимости у младших школьников
Для организации учебной деятельности учащихся начальных классов, направленной на эффективную подготовку к формированию представлений о функциональной зависимости должны выполняться следующие дидактические условия: наличие в курсе математики идей, непосредственно связанных с функциональными представлениями, таких как идея изменения, соответствия, закономерности и зависимости; наличие в содержании курса математики понятий, необходимых для осознанного усвоения понятия функции; создание проблемных ситуаций в процессе усвоения программного содержания; систематическое использование различных моделей (предметной, вербальной, символической, схематической и графической); использование учебных заданий, в основу которых положены приемы выбора, сравнения, преобразования и конструирования; организация целенаправленного наблюдения, сравнения, анализа и обобщения в процессе выполнения учебных заданий [4, с.110].
Для организации деятельности учащихся, направленной на формирование функциональных представлений и понятий, необходимых для восприятия и усвоения понятия «функция», целесообразно использовать учебные задания следующих видов: задания на тождественные преобразования числовых выражений (равенств) на основе смысла арифметического действия; на соотнесение предметной модели с числовым выражением (равенством); на соотнесение предметной, графической и символической моделей; на выявление закономерности; на установление соответствия между символическими моделями; на конструирование графической модели по заданной графической модели; на конструирование символической модели по заданной вербальной модели; на выбор символической модели, соответствующей вербальной модели; на конструирование числовых равенств по заданным условиям; на установление соответствия между символической и графической моделью; на выбор графической модели соответствующей символической модели; на преобразование на плоскости; на конструирование графической модели, соответствующей символической модели и т.д. [5, с.23].
Учебные задания, способствующие формированию функциональных представлений и понятий, необходимых для осознанного усвоения понятия функции, должны характеризоваться:
1) вариативностью;
2) неоднозначностью решений;
3) нацеленностью на формирование приемов умственной деятельности (таких, как анализ и синтез, сравнение, аналогия, классификация и обобщение);
4) отображением разнообразных закономерностей и зависимостей;
5) включенностью их в содержательную линию курса математики начальных классов [17, с.81].
На основе функциональных представлений разработаны учебные задания, направленные на их формирование:
1. Задания на формирование представлений об изменении и зависимости: на изменение результата арифметического действия в зависимости от изменения его компонентов; на использование основного свойства дроби; на классификацию числовых выражений (равенств) на основе их результата арифметического действия; тождественные преобразования числовых выражений (равенств) на основе смысла арифметического действия; на преобразование числовых выражений; на преобразование дробных выражений; на конструирование символической модели по заданной вербальной модели и др.).
Например, «Чем похожи все пары выражений? Найди их значения:
а) 89 + 47 б) 57+29 в) 76+57
90 + 47 57+30 76+60
Сравни равенства в каждой паре и сделай вывод».
2. Задания на формирование представления о закономерности, как правила, по которому записаны ряды чисел: на выявление закономерности.
Например, «Найди правила, по которым составлены ряды чисел:
а) 0,5; 0,05; 0,005; 0,0005; …;
б) 0,2; 0,4; 0,6; 0,8; …;
в) 0,12; 2,14; 4,16; 6,18; ….
Запиши в каждом ряду еще три числа по тому же правилу».
3. Задания на формирование представления о соответствии: на соотнесение предметной, графической и символической моделей; на установление соответствия между символическими моделями.
Например, «Соедини с числом 5 те выражения, значения которых делятся на 5, если а делится на 5».
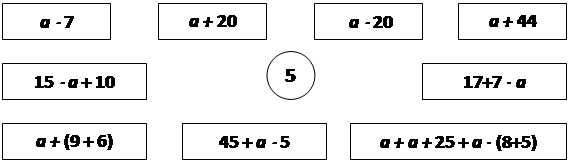
Эти учебные задания формулируются в основном на числовом материале, причем они усложняются и варьируются как по форме, так и по содержанию.
Решение задач на прямую и обратную пропорциональные зависимости посвящен решению текстовых задач на прямую и обратную пропорциональные зависимости арифметическим способом. Среди таких задач выделяются задачи, в которых числовые данные находятся в некотором отношении, что предполагает ещё один способ решения, представляющий интерес с точки зрения функциональной пропедевтики [36, с.105].
Кроме того, придать функциональный характер текстовым задачам можно с помощью дополнительных вопросов, направленных на изменение данных задачи, условия, вопроса, на соотнесение условия с различными выражениями и равенствами. Эти приемы помогают учащимся представить величины, рассматриваемые в задаче в движении, изменении, что позволяет формировать у учащихся функциональный стиль мышления.
На программном содержании курса математики начальных классов используются также учебные задания следующих видов:
1) задания на соотнесение предметной модели с числовым выражением (равенством);
2) задания на установление соответствия между символическими моделями;
3) задания на конструирование графической модели по заданной графической модели;
4) задания на конструирование символической модели по заданной вербальной модели;
5) задания на выбор символической модели, соответствующей вербальной модели;
6) задания на конструирование числовых равенств по заданным условиям;
7) задания на установление соответствия между символической и графической моделью;
8) задания на выбор графической модели, соответствующей символической модели;
9) задания на преобразование на плоскости;
10) задания на конструирование графической модели, соответствующей символической модели и т.д. [20, с.110].
Приведем примеры заданий:
1. Задание на конструирование числовых равенств по заданным условиям:
Выбери два отношения, из которых можно составить верное равенство. Запиши это равенство:
1,5 : 2; 3 : 6; 4,5 : 8; 6 : 8; 15 : 10.
2. Задание на конструирование графической модели, соответствующей символической модели:
Проверь, будут ли величины х и у прямо пропорциональными при данных значениях:
| х | 1 | 4 | 16 | 64 | 256 |
| у | 0,6 | 2,4 | 9,6 | 38,4 | 153,6 |
Если возникнут трудности при выполнении задания, то:
представь данную таблицу в таком виде:
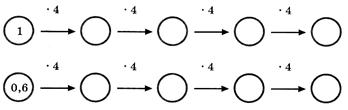
и найди отношения соответствующих значений величин х и у.
3. Задание на преобразование на плоскости:
Впиши пропущенные слова и числа, чтобы получились верные высказывания:
1) точка А (3; 4) при перемещении вправо на 2 единичных отрезка перешла в точку В (…;…);
2) точка L (5; -2) при перемещении______________на___единичных отрезков перешла в точку M (5; 2);
3) точка Х (1; 1) при перемещении вверх на 3 и вправо на 6 единичных отрезков перешла в точку У (…;…);
4) точка V (2; 3) при перемещении__________на___и___________ на___ единичных отрезков перешла в точку W (7; -2).
4. Задание на конструирование графической модели, соответствующей символической модели:
а) Выбери единичный отрезок и построй точки в координатной плоскости:
А (0,6; 0), В (0; ![]() ), С (0,1; 0,7), D
), С (0,1; 0,7), D ![]() , E
, E ![]() , К
, К ![]() .
.
б) Выбери единичный отрезок и построй точки в координатной плоскости:
А(600; 0), B(0; -300), C(100; 700), E(-500; -600), K(900; -400).
Все учебные задания, обладают следующими характеристиками: вариативностью; неоднозначностью решений; нацеленностью на формирование приемов умственной деятельности (таких, как анализ и синтез, сравнение, аналогия, классификация и обобщение); отображением разнообразных закономерностей и зависимостей; включенностью их в содержательную линию курса математики начальных классов [10, с.95].
Таким образом, рассмотрев теоретические основы формирования представлений о функциональной зависимости у младших школьников, мы пришли к выводу, что функциональная зависимость является одной из тех математических идей, которые способны объединить в единое целое все разделы математики, включенные в школьный курс. Функциональная зависимость отражает практическую направленность курса математики, взаимосвязь величин в естественнонаучных дисциплинах, а также формирует функциональное мышление школьников. Исходя из опыта обучения, известно, что понятие функции является абстрактным и довольно сложным для восприятия учащимися. Поэтому в процессе реализации данной линии необходимо усилить наглядность изучаемых объектов и понятий в рамках отведенного времени, предоставить учащимся возможность увидеть зависимость не только в виде статичной модели, но и в динамике, дать возможность учащимся непосредственно задавать, изменять и изучать функции при помощи интерактивных моделей, расширить систему задач при помощи упражнений, содержащих анимацию и элементы управления и т.д. Такому «живому» изучению функциональной зависимости может способствовать применение комплекса упражнений, направленных на формирование представлений о функциональной зависимости.
Следующая глава будет посвящена экспериментальной работе по формированию представлений младших школьников о функциональной зависимости.
Глава 2. Опытно-экспериментальная работа по формированию представлений о функциональной зависимости у младших школьников с применением комплекса упражнений
2.1 Диагностика уровней сформированности представлений младших школьников о функциональной зависимости
Для формирования представлений у младших школьников о функциональной зависимости на базе МОУ СОШ №31 города Ишима был проведен эксперимент.
В эксперименте приняли участие учащиеся 3 «А» (экспериментальная группа) и 3 «Б» (контрольная группа) классов в количестве по 20 человек в каждом классе. Список детей, участвующих в исследовании приведен в приложении 1.
Эксперимент состоял из трех этапов:
1 этап – констатирующий этап - диагностика уровня сформированности представлений о функциональной зависимости у младших школьников.
2 этап – формирующий этап - разработан и реализован комплекс упражнений, направленных на формирование представлений о функциональной зависимости у младших школьников.
3 этап – контрольный этап - проведен анализ эффективности занятий с применением комплекса упражнений, направленных на формирование представлений о функциональной зависимости у младших школьников.
Для выявления уровня сформированности представлений о функциональной зависимости у младших школьников были выделены следующие функциональные умения:
1) строить график функции;
2) записывать координаты точек;
3) находить наибольшее и наименьшее значения функции на заданном промежутке;
4) оперировать функциональной символикой.
На основе выделенных умений, а также для аналитической обработки результатов исследования и получения количественных показателей были выделены три уровня сформированности представлений о функциональной зависимости у младших школьников: низкий, средний и высокий.
С целью определения уровня сформированности представлений о функциональной зависимости у младших школьников в ходе констатирующего эксперимента организовывались беседы с учащимися 3-х классов, проводились контрольные работы, по результатам выполнения которых выявлялись трудности, возникающие у учащихся при усвоении понятия функции, функциональной зависимости.
Чтобы оценить способность учащихся применять функциональные умения для решения практических задач им были предложены ситуационные задачи. В силу своей межпредметности, интегративности ситуационные задачи способствуют систематизации предметных знаний на деятельностной практико-ориентированной основе, когда ученики, осваивая универсальные способы деятельности, решают личностно-значимые проблемы с использованием предметных знаний. Следует отметить, что в процессе обучения математике учащиеся ни экспериментального, ни контрольного классов с такими задачами не встречались.
Приведем пример одной из ситуационных задач, которые предлагались учащимся:
Задача. «Эти простые – непростые зависимости»
Каждый слышал поговорку: «Как аукнется, так и откликнется». А ты замечал на себе проявление такой закономерности?
Текст 1. Маша и Миша решили посадить одновременно цветы, чтобы подарить их маме к 8 марта. В течение 12 недель Маша поливала цветок регулярно, а Миша иногда забывал. Высота цветка Маши в конце каждой недели представлена в таблице 1:
| Неделя, t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Высота цветка, h (см) | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
Текст 2. Существуют различные шкалы для измерения температуры. Для перевода температуры, измеренной в градусах Цельсия, в градусы Фаренгейта пользуются формулой ![]() , где С – число градусов по шкале Цельсия, а F – число градусов по шкале Фаренгейта. Для каждого значения температуры по Цельсию с помощью этой формулы можно найти соответствующее значение температуры по шкале Фаренгейта.
, где С – число градусов по шкале Цельсия, а F – число градусов по шкале Фаренгейта. Для каждого значения температуры по Цельсию с помощью этой формулы можно найти соответствующее значение температуры по шкале Фаренгейта.
Задания.
1. Пользуясь таблицей роста цветка Маши, составь таблицу роста цветка Миши, учитывая, что его цветок рос в два раза медленнее (из-за забывчивости Миши).
2. Найди высоту цветка Миши через 3,5 недели. Опиши процесс нахождения ответа на вопрос.
3. Составь таблицу перевода значений температуры из градусов по Цельсию в градусы по Фаренгейту (для значений от 0° С до 30° С).
4. Выяви зависимости, описанные в тексте 1 и тексте 2. Сравни их.
5. Предложи жизненные ситуации, в которых проявляются закономерности, выявленные тобой из анализа текста 1 и 2.
Проанализировав результаты работ учащихся по четырем умениям, можно прийти к следующим выводам:
- учащиеся как 3 «А», так и 3 «Б» классов понимают представленную информацию, предлагают способы решения проблемы, но при обосновании способа решения учащиеся 3 «А» класса в меньшей степени оперируют функциональными представлениями;
- учащиеся 3 «А класса при выполнении задания, где нужно было привести примеры зависимостей, аналогичных тем, что были предложены в задаче, приводят примеры таких зависимостей, т.е. зависимостей, которые являются функциональными, в то время как учащиеся 3 «Б» класса предлагают зависимости, исходя из своего представления о них.
Таким образом, большее количество учащихся 3 «А» класса слабо оперирует функциональными представлениями и не способно применить сформированные функциональные умения для решения новых практических задач.
Данные констатирующего этапа эксперимента приведены в таблице 2.
Таблица 2
Показатели уровня сформированности представлений о функциональной зависимости у младших школьников по критериям на констатирующем этапе эксперимента
| Класс | Функциональные умения младших школьников | |||||||||||
| строить график функции | записывать координаты точек | находить наибольшее и наименьшее значения функции на заданном промежутке | оперировать функциональной символикой | |||||||||
| Низкий уровень | Средний уровень | Высокий уровень | Низкий уровень | Средний уровень | Высокий уровень | Низкий уровень | Средний уровень | Высокий уровень | Низкий уровень | Средний уровень | Высокий уровень | |
| 3 «А» класс | 5 | 14 | 1 | 4 | 15 | 1 | 4 | 14 | 2 | 3 | 16 | 1 |
| 3 «Б» класс | 1 | 16 | 3 | - | 13 | 7 | 1 | 14 | 5 | 2 | 15 | 3 |
В результате проведенной работы на констатирующем этапе эксперимента было установлено, что 30% всех испытуемых имеют низкий уровень сформированности представлений о функциональной зависимости, исходя из четырех критериев, определенных в начале эксперимента, 57 % испытуемых показали средний уровень и лишь 13% младших школьников имеют высокий уровень сформированности представлений о функциональной зависимости.
Анализ полученных результатов позволил сделать вывод о том, что большая часть младших школьников имеет средний и низкий уровень сформированности представлений о функциональной зависимости и нуждается в коррекции. Следовательно, результаты констатирующего этапа исследования требуют проведения формирующего этапа эксперимента в соответствии с предложенной гипотезой.
Похожие работы
... тематически. Таким образом, разработанное методическое пособие направит работу учителя на формирование позитивного взаимоотношения. 2.3 Выводы по главе II Раскрыв приемы психолого-педагогического взаимодействия учителя и ученика в конфликтных ситуациях мы выделили три основных подхода, применяемых в работе с учениками при нарушении дисциплины: «руки прочь», подход «твердой руки», « ...
... сложившимися к настоящему времени режимами работы с компьютером, игровым, экспериментным, обучающим, программно-творческим. Глава II. Методика развития алгоритмического мышления младших школьников на уроках информатики 2.1 Алгоритмическое мышление и методы его развития Коль скоро в целях обучения информатике заявлено развитие системного, аналитического и алгоритмического мышления, то ...
... и умения, но и определенный социальный статус. Меняются интересы, ценности ребенка, весь уклад его жизни. 3. Комплекс педагогических условий формирования умений учебной деятельности младших школьников Успех педагогической деятельности в значительной мере зависит от характера сложившихся взаимоотношений между учителем и обучаемыми. Анализ и обобщение психолого-педагогических исследований по ...
... школе всех видов грамматических навыков может существенно различаться в зависимости от используемых технологий и приемов обучения. Комплекс упражнений, направленных на формирование иноязычных грамматических навыков у учащихся вторых классов на основе грамматических сказок При составлении комплекса упражнений нами были выделены следующие темы, представляющие для учащийся значительные трудности: ...



0 комментариев