Навигация
Реализация комплекса упражнений, направленных на формирование представлений о функциональной зависимости у младших школьников
2.2 Реализация комплекса упражнений, направленных на формирование представлений о функциональной зависимости у младших школьников
С целью формирования у младших школьников представлений о функциональной зависимости нами был проведен формирующий этап эксперимента, в котором приняли участие только учащиеся экспериментального 3 «А» класса. Для этого нами применялся комплекс подобранных для этой цели упражнений, направленных на формирование функциональной зависимости у младших школьников. Изучение проводилось по теме школьного курса математики «Зависимость между результатами и компонентами арифметических действий». По теме проводилось пробное и основное исследование.
Зависимость между элементами арифметических действий изучалась каждым из испытуемых в индивидуальном порядке под руководством экспериментатора один раз, затем второй, третий, — так до полного овладения ею. В конце исследования-обучения давалась в индивидуальном порядке контрольная работа.
Изучение зависимости между элементами геометрических фигур проводилось в течение нескольких уроков. Сначала учащиеся знакомились с простейшими случаями зависимости между площадью и стороной прямоугольника при постоянной величине смежной стороны. Затем — с зависимостью между сторонами и площадью квадрата. И, наконец, со школьниками велись занятия-исследования по обучению их пониманию и усвоению зависимости между основанием, высотой и площадью прямоугольника, параллелограмма и треугольника при постоянной величине суммы их основания и высоты.
Все занятия проводились в индивидуальном порядке. В конце исследования-обучения в индивидуальном же порядке давалась контрольная работа.
По теме «Зависимость между компонентами и результатами действий» работа проводилась следующим образом.
Группа изучала материал в таком порядке изменение суммы, затем — изменение произведения, далее — изменение разности и, наконец, — изменение частного.
Затем группа изучала материал в том же порядке, но в одновременном противопоставлении изменению компонентов изменения результатов действий.
И, наконец, группа изучала материал в следующем порядке: изменение суммы, затем — изменение разности, далее — изменение произведения и, наконец, — изменение частного.
Для изучения зависимости между изменением площади и изменением входящих и ее выражение компонентов были созданы группы, работавшие:
Первая группа — с графиками.
Вторая группа — с графиками + наглядное изображение образа меняющейся фигуры в тетради
Третья группа — с диаграммами.
Четвертая группа — с наглядным изображением образа меняющейся фигуры в тетради
В изучении зависимости между элементами действии ученик пользуется конкретным примером. Он постепенно переходит от использования данного единичного примера, как необходимого в выражении зависимости, к использованию его, как возможного для выражения разбираемой зависимости.
В активной деятельности с вариативным использованием примеров ученик в процессе обучения доходит до понимания и усвоения обобщенного характера изменения зависимых величин, от «живого созерцания» он поднимается к «абстрактному мышлению» и затем конкретизирует обобщенные знания в практическом применении. Все это связано с совершенствованием анализа и синтеза в совместной деятельности первой и второй сигнальных систем при ведущей роли второй, словесной системы мозговой коры.
При решении задач в первое время ученики не осмысливали их на базе заключенной в них функциональной зависимости, за внешним оформлением не вскрывали сущности изученной уже в принципе ими зависимости. Обобщающая и конкретизирующая деятельность реализовалась лишь применительно к заданиям — примерам. Она не переносилась на решение задач. Развитие умения переосмысливать решение примеров на основе функциональной зависимости в дальнейшей работе ученика, в связи с совершенствованием избирательной иррадиации и развитием подвижности мозговых процессов, переносилось и на решение задач.
В исследовании обнаружилось смешение школьниками разностных и кратных изменений, происходящих в зависимых величинах. Это обусловливалось там, что на предыдущих этапах обучения изучение этих изменений проводилось без надлежащего использования сравнения, особенно сравнения в виде противопоставления.
При изучении обратной зависимости изменения ученики обычно на первых занятиях обратную зависимость подменяли прямою, а количественное изменение устанавливали подбором. Выработанный стереотип понимания отношения между величинами прямого изменения переносился на выполнение задания с обратным изменением. В процессе дальнейшей систематической работы понимание обратной зависимости учениками совершалось от частичного привнесения обратного изменения в прямую зависимость к полной замене прямой зависимости обратной.
Формирование понимания зависимости происходило только в непосредственной деятельности с заданием. Часто первичное восприятие задания приводило к ошибочному его выполнению. Дальнейшая работа над заданием раскрывала перед учеником существенные связи, сначала им незамеченные.
Понимание зависимости между изменением одного компонента и изменением результата действия совершается сначала в динамике качественного изменения. Количественная отдифференцированность изменения происходит позднее, причем в изменении разности и частного она носит более сложный характер и требует для понимания больше усилий, чем в изменении суммы и произведения. Это первая ступень в понимании зависимости между компонентами и результатами действия.
Затем школьники поднимаются к пониманию и усвоению зависимости между изменением обоих компонентов и изменением результата действия. На этой второй ступени в понимании зависимости школьники проходят несколько этапов.
На первом этапе работы все задание по установлению зависимости между тремя элементами выполнялось школьниками обычно неверно. Они не могли еще осмыслить полностью одновременное изменение трех величин.
Понимание зависимости начиналось с выяснения качественного характера изменения величин.
Понимание изменений в сложении и умножении наступало раньше, чем в вычитании и делении.
Обратная зависимость на этом этапе работы не понималась.
На втором этапе этой ступени в отличие от первого этапа заданные изменения понимались учеником как проявление функциональной зависимости. Выполнялись все предложенные изменения не как арифметические действия над заданными числами, а как результативные изменения величин, зависимых от заданных изменений других величин.
Однако на этом этапе работы обнаружился ряд трудностей, специфичных для понимания сложного характера изменения элементов вычитания и деления, в силу чего качественное и количественное изменения элементов этих действий нередко определялось неверно.
На следующем этапе наступало понимание вариативности изменения между качественным характером поведения зависимых величин и их количественным выражением. Для действий сложения и вычитания расхождений не обнаруживалось.
При изучении вариативных изменений в действиях умножении и делении характер изменения иногда отрывался учеником от количественного выражения, и, обычно уменьшение выполнялось вычитанием, а увеличение — сложением.
В действиях вычитания и деления обнаружился отрицательный перенос изменения последнего компонента на изменение результата действия. Старые связи, отношения, образовавшие стереотипную систему изменений в сложении и умножении, тормозили понимание новых отношений и формирование новых связей.
Наконец, на третьей ступени школьники начинали понимать обратный характер зависимости между элементами арифметических действий. Понимание обратной зависимости для каждого действия шло через использование прямого характера изменения. Понимание обратной зависимости для всех арифметических действий при решении примеров и задач происходила медленнее, чем понимание прямой зависимости.
Овладение зависимостью между компонентами и результатами действий выразилось в развитии у школьников тесной связи абстрагирующей и конкретизирующей мыслительной работы. Сформировавшиеся обобщенные, понятийные знания о зависимости между элементами действий школьники начинали умело применять к решению новых примеров и задач, к самостоятельному составлению примеров и задач на заданную зависимость. Школьники начинали понимать рациональное значение применения понятийного знания зависимости к решению конкретных арифметических задач.
При изучении зависимости между элементами геометрических фигур ученик стремился представить себе наглядный образ изменяющейся фигуры. Но ввиду ограниченности геометрических знаний образ фигуры оказывается у него неподвижным, статическим, лишенным изменений.
На начальных этапах изучения зависимости между величинами геометрической фигуры понимание ее происходило не через соотношение элементов конкретного, разбираемого образа. Сначала зависимость в ее понятийном содержании понималась через известный и более простой математический материал, через активизацию знаний и пришлого опыта. Затем полученное понятийное знание зависимости соответственно выражалось в наглядных образах.
Привлечение наглядного образа играет двоякую роль: оно может и помогать, облегчать установление заключенной в задаче зависимости, а может мешать, заслонять ее. Отрицательная роль наглядных образов проявляется тогда, когда они говорят ученику лишь об отдельных частных случаях разбираемой зависимости.
Для проверки эффективности реализованного комплекса упражнений, направленных на формирование представлений о функциональной зависимости у младших школьников, нами была проведена повторная диагностика уровней сформированности представлений о функциональной зависимости школьников экспериментальной и контрольной групп.
Методика контрольного обследования совпадала с методикой констатирующего обследования уровня сформированности представлений о функциональной зависимости. Данные контрольного этапа эксперимента по проведенной диагностике в экспериментальной и контрольной группах испытуемых приведены в таблице 3. Результаты анализировались с привлечением данных констатирующего обследования уровня сформированности представлений о функциональной зависимости.
Таблица 3
Показатели уровня сформированности представлений о функциональной зависимости в экспериментальной группе на контрольном этапе эксперимента
| Уровень сформированности представлений о функциональной зависимости | Количество наблюдений | % |
| Низкий | 0 | 0 |
| Средний | 7 | 70 |
| Высокий | 3 | 30 |
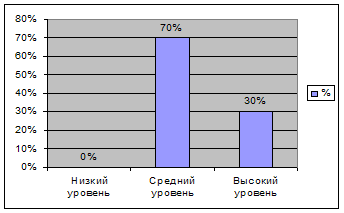
Для наглядности показатели уровня сформированности представлений о функциональной зависимости в экспериментальной группе на контрольном этапе эксперимента представлены на рисунке 1.
Таблица 4
Показатели уровня сформированности представлений о функциональной зависимости в контрольной группе на контрольном этапе эксперимента
| Уровень сформированности представлений о функциональной зависимости | Количество наблюдений | % |
| Низкий | 2 | 20 |
| Средний | 5 | 50 |
| Высокий | 3 | 30 |
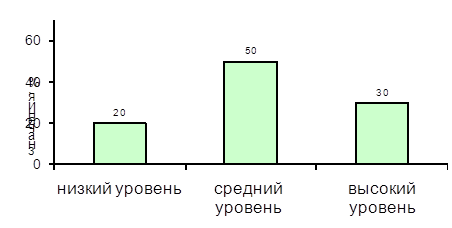 Для наглядности показатели уровня сформированности представлений о функциональной зависимости в контрольной группе на контрольном этапе эксперимента представлены на рисунке 2.
Для наглядности показатели уровня сформированности представлений о функциональной зависимости в контрольной группе на контрольном этапе эксперимента представлены на рисунке 2.
Оценка динамики изменения уровня сформированности представлений о функциональной зависимости в экспериментальной группе на констатирующем и контрольном этапах эксперимента представлена в таблице 5.
Таблица 5
Показатели уровня сформированности представлений о функциональной зависимости в экспериментальной группе на констатирующем и контрольном этапах эксперимента
| Уровень сформированности представлений о функциональной зависимости | Констатирующий этап (%) | Контрольный этап (%) |
| Низкий | 20 | 0 |
| Средний | 60 | 70 |
| Высокий | 20 | 30 |
Для наглядности представим сравнительный анализ уровня сформированности представлений о функциональной зависимости в экспериментальной группе на констатирующем и контрольном этапе на рисунке 3.
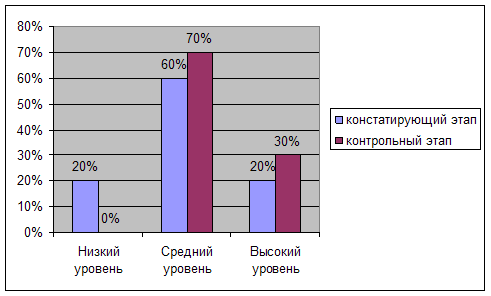
Рис.3 Сравнительный анализ уровня сформированности представлений о функциональной зависимости в экспериментальной группе на констатирующем и контрольном этапе
Сравнение данных констатирующего этапа с данными, полученными на контрольном этапе показывает, что количество школьников с низким уровнем сформированности представлений о функциональной зависимости уменьшилось до 0, на 10 % увеличилось количество школьников, имевших средний уровень сформированности представлений о функциональной зависимости. За счет уменьшения количества низкого уровня сформированности представлений о функциональной зависимости на 10% увеличилось количество школьников, показавших высокий уровень сформированности представлений о функциональной зависимости. В целом, это доказывает, что содержание и приемы формирующего этапа эксперимента были выбраны правильно и оказались эффективными для повышения уровня сформированности представлений о функциональной зависимости у младших школьников.
Незначительные изменения уровня сформированности представлений о функциональной зависимости контрольной группы, выявленные на контрольном этапе: уменьшение на 10% школьников с высоким и увеличение на 10% с низким уровнем сформированности представлений о функциональной зависимости, средний уровень сформированности представлений о функциональной зависимости без изменений подтверждает предположения, что без применения упражнений достижение существенного изменения сформированности представлений о функциональной зависимости у младших школьников весьма затруднительно.
Сравнительный анализ уровня сформированности представлений о функциональной зависимости экспериментальной и контрольной групп на контрольном этапе эксперимента представлен в таблице 6.
Таблица 6
Показатели уровня сформированности представлений о функциональной зависимости экспериментальной и контрольной групп на контрольном этапе эксперимента
| Уровень сформированности представлений о функциональной зависимости | Экспериментальная группа (%) | Контрольная группа (%) |
| Низкий | 0 | 20 |
| Средний | 70 | 50 |
| Высокий | 30 | 30 |
Таким образом, контрольный этап эксперимента позволил прийти к выводу о том, что для формирования представлений о функциональной зависимости у младших школьников необходимо разрабатывать и применять упражнения, направленные на формирование представлений о функциональной зависимости.
Заключение
Одним из видов объективно существующих связей является математическая функциональная зависимость.
Понятие функциональной зависимости является одним из основных понятий всей математики, в том числе и элементарной. Если одна величина стоит в зависимости от другой, то при изменении последней (независимого переменного), первая (т. е. функция) будет изменяться по известному закону; таким образом, каждое частное значение независимого переменного вполне определяет соответствующее значение функции.
Школьные программы должны быть построены так, чтобы идеи переменной величины и функциональной зависимости, являющиеся прямым математическим выражением основных черт диалектического миропонимания, как можно ранее усваивались учащимися и как можно ранее становились основным стержнем всего школьного курса математики.
В нашем исследовании мы рассмотрели понятие «функциональная зависимость» в методической литературе, выявили педагогические идеи преподавания функциональной зависимости в начальной школе, изучили виды упражнений, направленных на формирование представлений о функциональной зависимости у младших школьников.
Для исследования и проверки эффективности комплекса подобранных нами упражнений для формирования представлений о функциональной зависимости нами было проведена опытно-экспериментальная работа. На констатирующем этапе исследования нами был определен уровень сформированности представлений о функциональной зависимости у младших школьников. Было установлено, что большинство учащихся 3 классов имеют низкий уровень сформированности представлений о функциональной зависимости. Для формирования представлений нами был проведен формирующий этап эксперимента, на котором нами были использованы упражнения, направленные на формирование представлений о функциональной зависимости. Контрольный этап экспериментального исследования показал, что в результате формирующего этапа уровень сформированности представлений о функциональной зависимости у младших школьников экспериментальной группы значительно изменился.
Таким образом, задачи, поставленные в начале работы, нами были решены, цель исследования достигнута, гипотеза подтверждена.
Библиография
1. Аматова, Г.И. Математика [Текст]/Г.И. Аматова, М.А. Аматов. -М.: Московский психолого-социальный институт, 1999. – 337 с.
2. Аммосова, Н.В. Понятие функциональной зависимости в начальной школе [Текст] / Аммосова Н.В. // Начальная школа. - 2000. - №5.- С.109-114.
3. Байрамукова, П.У. Внеклассная работа по математике [Текст] / П.У. Байрамукова. – М.: Издат-школа «Райл», 1997. – С.214.
4. Бантова, М.А. Методика преподавания математики в начальных классах [Текст] /М.А. Бантова, Г.В. Бельтюкова. – М.: Просвещение, 1984. – 335 с.
5. Боцманова, М.Э. Психологические вопросы применения графических схем учащимися начальной школы [Текст]/М.Э. Боцманова// Вопросы психологии. – 1960. – №5.
6. Виленкин, Н.Я. Задачник практикумом по математике [Текст] / Н.Я.Виленкин, Н.Н.Лаврова, В.Б.Рождественская, Л.П. Стойлова. – М.: Просвещение, 1985. – С.142.
7. Виленкин, Н.Я. Математика [Текст]/Н.Я. Виленкин, Л.М. Пышкало, В.Б. Рождественская, Л.И. Стойлова. – М.: Просвещение, 1977. – С.220.
8. Зак, А.З. 600 игровых задач для развития логического мышления детей [Текст] /А.З. Зак. - Ярославль: Академия развития, 1998. – 175 с.
9. Истомина, Н.Б. Активизация учащихся на уроках математики в начальных классах: Пособие для учителя [Текст]/Н.Б. Истомина.– М.: Просвещение, 1985. –– 64 с.
10. Истомина, Н.Б. и др. Практикум по методике преподавания математики в начальных классах [Текст]/ Н.Б. Истомина, Л.Г. Латохина, Г.Г. Шмырева. – М.: Просвещение, 1986. – 176 с.
11. Истомина, Н.Б. Методика обучения математике в начальных классах [Текст] /Н.Б. Истомина. - М.: ACADEMA, 2000. – 453 с.
12. Истомина, Н.Б. Методика обучения математике в начальных классах [Текст] /Н.Б. Истомина. – М.: Издательский центр «Академия», 1998. – 288 с.
13. Котов, А.Я. Вечера занимательной математики [Текст]/А.Я.Котов. – М.: Просвещение, 1967. – С.117.
14. Крутецкий, В.А. Психология математических способностей школьников [Текст] /В.А. Крутецкий. – М.: Просвещение,1968. – 432 с.
15. Кульневич, С.В. Нетрадиционные уроки в начальной школе [Текст] / С.В. Кульневич, Т.П. Лакоценина. — Ростов н/Д: ТЦ «Учитель», 2002. – 375 с.
16. Марушенко, Л.Ю. Арифметическая задача как средство формирования первых функциональных представлений у учащихся [Текст] / Л.Ю. Марушенко // Новые технологии в обучении физике, математике и информатике: материалы региональной научно-практической конференции, посвященной памяти чл.-корр. РАЕН, проф., доктора педагогических наук А.А. Пинского. – Благовещенск: Издательство БГПУ, 2007. – С. 107 - 115.
17. Марушенко, Л.Ю. К вопросу об изучении функций в школе [Текст]/Л.Ю. Марушенко//Новые технологии в обучении физике, математике и информатике: материалы региональной научно-практической конференции, посвященной памяти чл.-корр. РАЕН, проф., доктора педагогических наук А.А. Пинского. – Благовещенск: Издательство БГПУ, 2005. - С. 81-83.
18. Марушенко, Л.Ю. К проблеме изучения понятия функции в школьном курсе математики [Текст] /Л.Ю. Марушенко// Актуальные вопросы методики преподавания математики и информатики в свете модернизации Российского образования: сборник научных трудов Всероссийской научно-практической конференции, 17 апреля 2006 г. – Биробиджан: Изд-во ДВГСГА, 2006. – 263 с.
19. Марушенко, Л.Ю. Об оценке качества усвоения понятия функции учащимися старших классов [Текст] / Л.Ю. Марушенко // Новые технологии в обучении физике, математике и информатике: материалы региональной научно-практической конференции, посвященной памяти чл.-корр. РАЕН, проф., доктора педагогических наук А.А. Пинского. – Благовещенск: Издательство БГПУ, 2008. - С. 121-125.
20. Марушенко, Л.Ю. Пропедевтика функциональной зависимости в курсе математики средней школы [Текст] / Л.Ю. Марушенко// Новые технологии в обучении физике, математике и информатике: материалы региональной научно-практической конференции, посвященной памяти чл.-корр. РАЕН, проф., доктора педагогических наук А.А. Пинского. – Благовещенск: Издательство БГПУ, 2006. - С. 110-111.
21. Марушенко, Л.Ю. Функциональный подход к решению текстовых задач на прямо пропорциональную зависимость [Текст]/Л.Ю. Марушенко// Начальная школа. - 2007. - №7. – С. 44-51.
22. Методика начального обучения математике / под ред. Л.Н. Скаткина. – М.: Просвещение, 1972. – 320 с.
23. Методика начального обучения математике. Под общей редакцией А.А. Столяра и В.Л. Дрозда. Минск: Вышэйшая школа, 1988. – 234 с.
24. Методика начального обучения математике: Учеб. пособие для пед. ин-тов / В.Л. Дрозд, А.Т. Касатонова, Л.А. Латотин и др.; Под общ. ред. А.А. Столяра, В.Л. Дрозда. – Мн.: Выш. шк., 1988. – 254 с.
25. Моро, М.И. Методика обучения математике I-III классах [Текст] / М.И. Моро, А.М. Пышкало. - М.: Просвещение, 1978. – 321 с.
26. Остер, Г.Б. Задачник [Текст]/Г.Б.Остер. – М.: Спарк-М, 1995. – 116с.
27. Пойа, Д. Как решать задачу [Текст]/Д.Пойа. – М.: Учпедгиз, 1959. – 216 с.
28. Программы общеобразовательных учреждений. Начальные классы (1-4). Часть I. - М.: Просвещение, 2001. – 432 с.
29. Сорокин, П.И. Занимательные задачи по математике [Текст] / П.И.Сорокин. – М.: Просвещение, 1967. – 229 с.
30. Стойлова, Л.П. Математика [Текст]/Л.П. Стойлова.- М.: Академия, 2000. – С.226.
31. Стойлова, Л.П. Основы начального курса математики [Текст] / Л.П. Стойлова, А.М. Пышкало. – М.: Просвещение, 1988.– 320 с.
32. Труднев, В.П. Внеклассная работа по математике в начальной школе [Текст] /В.П. Труднев. – М.: Просвещение, 1975. – 335 с.
33. Труднев, В.П. Считай, смекай, отгадывай! [Текст]/В.П. Труднев. – М.: Просвещение, 2004. – С.128.
34. Учебное пособие по математике для педагогических факультетов. Под редакцией Мерзона- М.: Московский псих.-соц. институт, 1999. – С.28.
35. Формирование элементарных математических представлений у дошкольников / под редакцией А.А. Столяра. – М.: Просвещение, 1988. – 303 с.
36. Фридман, Л.М. Как научиться решать задачи [Текст]/Л.М. Фридман, Е.Н. Турецкий. – М.: Просвещение, 1989. – 192 с.
37. Эрдниев, П.М., Эрдниев Б.П. Теория и методика обучения математике в начальной школе [Текст]/П.М. Эрдниев, Б.П. Эрдниев. – М.: Педагогика, 1988. – 208 с.
Похожие работы
... тематически. Таким образом, разработанное методическое пособие направит работу учителя на формирование позитивного взаимоотношения. 2.3 Выводы по главе II Раскрыв приемы психолого-педагогического взаимодействия учителя и ученика в конфликтных ситуациях мы выделили три основных подхода, применяемых в работе с учениками при нарушении дисциплины: «руки прочь», подход «твердой руки», « ...
... сложившимися к настоящему времени режимами работы с компьютером, игровым, экспериментным, обучающим, программно-творческим. Глава II. Методика развития алгоритмического мышления младших школьников на уроках информатики 2.1 Алгоритмическое мышление и методы его развития Коль скоро в целях обучения информатике заявлено развитие системного, аналитического и алгоритмического мышления, то ...
... и умения, но и определенный социальный статус. Меняются интересы, ценности ребенка, весь уклад его жизни. 3. Комплекс педагогических условий формирования умений учебной деятельности младших школьников Успех педагогической деятельности в значительной мере зависит от характера сложившихся взаимоотношений между учителем и обучаемыми. Анализ и обобщение психолого-педагогических исследований по ...
... школе всех видов грамматических навыков может существенно различаться в зависимости от используемых технологий и приемов обучения. Комплекс упражнений, направленных на формирование иноязычных грамматических навыков у учащихся вторых классов на основе грамматических сказок При составлении комплекса упражнений нами были выделены следующие темы, представляющие для учащийся значительные трудности: ...



0 комментариев