Навигация
Чтобы найти число по его дроби, можно разделить на эту дробь число, ей соответствующее
1. Чтобы найти число по его дроби, можно разделить на эту дробь число, ей соответствующее.
2. Чтобы найти дробь от числа, можно это число умножить на данную дробь.
В одном из разделов "Для тех, кому интересно" имеются старинные задачи на дроби.
В учебнике [12] большое внимание уделяется задачам на движение: на нахождение собственной скорости катера; пути пройденного катером по течению реки и против; пути вертолета при попутном ветре, при встречном ветре за определенный промежуток времени. Также присутствуют задачи, которые имеют сказочный сюжет. Например: Вини-Пух вышел из дома Пяточка к дому Кристофера Робина. Он проходит за 1 мин 50 м. Через две минуты вслед за ним вышел Пятачок, который за 1 мин проходит 60 м. На каком расстоянии от дома Пяточка находиться дом Кристофера Робина, если они пришли туда одновременно?
В учебнике [13] класса отдельно выделены параграфы для перевода задачи на математический язык и на составление математической модели. Уделяется большое внимание задачам на проценты, которые имеют разный сюжет: сборка урожая; вычисление заработной платы; нахождение площади, отведенной под сельскохозяйственные культуры; определение количества учащихся, посещающих разные кружки, студии и секции; определение количества монет в коллекции нумизмата, марок в коллекции филателиста. Имеются сюжетные задачи на деление фруктов на части.
В учебнике [14] встречаются самые разнообразные сюжеты: масса учебников и их количество (имеется в виду учебник определенного наименования); средняя скорость движения и проделанный за определенное время путь; время движения и путь, проделанный с определенной скоростью; средняя скорость движения и время на преодоление определенного расстояния; рост человека и его масса; высота предмета в данной точке земли и тень, которую он отбрасывает при конкретном времени в ясную погоду.
В учебниках [13, 14] используются алгебраический и арифметический способы решения задач.
Авторы Г.В. Дорофеев, Л.Г. Петерсон в своем учебнике "Математика 5 класс" (в 2 частях) посвятили целый параграф на перевод задачи на математический язык и на составление математической модели. Выделен пункт на решение задач на дроби. Присутствуют задачи на совместную работу. Задачи решаются арифметическим способом.
В учебнике [18] рассматриваются задачи на движение по реке, на нахождение процента от числа, на нахождение числа по его проценту, на простой процентный рост, на сложный процентный рост, на нахождение среднего арифметического, на смеси и сплавы. Сюжеты в учебниках [17, 18] самые разнообразные: определение времени наполнения водоема, бассейна; определение времени пошива одежды; определение времени уборки снега; нахождение массы продуктов; определение процентного содержание ингредиента в продукте; нахождение времени, скорости полета насекомых; нахождение расстояния между пунктами и т.д. Задачи решаются арифметическим и алгебраическим способами.
Таким образом, проанализировав учебники [11, 12, 13, 14, 15, 16, 17, 18] мы можем сказать, что сюжеты задач схожи. Сюжетные задачи - это наиболее традиционный вид математических задач. Они всегда занимали одно из ведущих мест в обучении математике, так как их функции в обучении весьма значительны, и среди них одна из важнейших - методологическая, суть которой заключается в том, что с помощью с сюжетных задач обучаемый может познавать реальную действительность, осознавать те знания и умения, которые необходимы при решении любых задач, а не только сюжетных.
1.3 Методика обучения решению сюжетных задач в курсе математики 5-6 классов
Сюжетной задачей называют такую задачу, в которой данные и связь между ними включены в фабулу. Содержание сюжетной задачи чаще всего представляет некоторую ситуацию, более или менее близкую к жизни. Эти задачи важны главным образом для усвоения учащимися математических отношений, для овладения эффективным методом познания - моделирование, для развития способностей, интереса учащихся к математике.
Большое значение при обучении математике имеет формирование общего приема решения задач. Но анализ практики показывает, что основное внимание уделяется ознакомлению со специальными способами решения отдельных типов задач. Это часто приводит к тому, что учащиеся не приобретают умения самостоятельно анализировать и решать различные типы задач. Поэтому проблема овладения общим приемом решения задач продолжает оставаться актуальной и должна разрабатываться в методике обучения математике.
Общий прием решения задач включает: знание этапов решения, методов (способов) решения, типов задач, обоснование выбора способа решения на основании анализа текста задачи, а также владение предметными знаниями: понятиями, определениями терминов, правилами, формулами, логическими приемами и операциями.
К этапам решения можно отнести:
1) анализ текста задачи;
2) перевод текста на язык математики;
3) установление отношений между данными и вопросом;
4) составление плана решения задачи;
5) осуществление плана решения;
6) проверка и оценка решения задачи.
Анализ текста задачи.
Работа над текстом задачи включает семантический, логический и математический анализ.
1. Семантический анализ направлен на обеспечение понимания содержания текста и предполагает:
выделение и осмысление:
отдельных слов, терминов, понятий, как житейских, так и математических,
грамматических конструкций ("если… то", "после того, как…" и т.д.),
количественных характеристик объекта, задаваемых словами "каждого", "какого-нибудь", "любое", "некоторое", "всего", "все", "почти все", "одинаковые", "столько же", "поровну" и т.д.;
восстановление предметной ситуации, описанной в задаче, путем упрощенного пересказа текста с выделением только существенной для решения задач информации;
выделение обобщенного смысла задачи - о чем говорится в задаче, указание на объект и величину, которая должна быть найдена (стоимость, объем, площадь, количество и т.д.)
2. Логический анализ предполагает:
умение заменять термины их определениями;
выводить следствия из имеющихся в условии задачи данных (понятия, процессы, явления).
3. Математический анализ включает анализ условия и требования задачи.
Анализ условия направлен на выделение:
а) объектов (предметов, процессов);
б) величин, характеризующих каждый объект;
в) характеристик величин (числовые значения, известные и неизвестные данные, отношения между известными данными величин).
Анализ требования направлен на выделение:
неизвестных количественных характеристик величин объектов или объекта.
Перевод текста на язык математики.
В результате анализа задачи текст задачи записывают кратко с использованием условной символики. После того как данные задачи специально вычленены в краткой записи, следует перейти к анализу отношений и связей между этими данными.
Для этого осуществляется перевод текста на язык графических моделей различного вида: чертеж, схема, график, таблица, символический рисунок, формула, уравнение и др. Перевод текста в форму модели позволяет обнаружить в нем свойства и отношения, которые часто трудно выявить при чтении текста.
Выполненный чертеж (рисунок) по тексту задачи позволяет фиксировать ход рассуждений при ее решении, что способствует формированию общих подходов к решению задач.
Поэтому к выполнению чертежей нужно предъявлять требования: они должны быть наглядными, четкими, соответствовать тексту задачи; на них должны быть отражены по возможности все данные, входящие в условие задачи; выделенные на них данные и искомые должны соответствовать условию задачи и общепринятым обозначениям.
Формирование умения выполнять чертеж задачи будет успешным, если учащиеся будут уметь читать соответствующий чертеж.
В связи с этим учащимся нужно предлагать упражнения на составление текста задачи по чертежу, рисунку.
Установление отношений между данными и вопросом.
Реализация этого компонента общего приема решения задач предусматривает установление отношений между:
данными условия,
данными вопроса,
данными условия и вопросом задачи.
На основе анализа условия и вопроса задачи определяется способ решения задачи (вычислить, построить, доказать), выстраивается последовательность конкретных действий.
При этом устанавливается достаточность, недостаточность или избыточность данных.
Выделяются четыре типа отношений между объектами и их величинами: равенство, часть/целое, разность, кратность, сочетание которых определяет разнообразие способов решения задач.
Примером такого отношения является формула а b=c, имеющая большое число разнообразных проявлений (связь пройденного пути, времени и скорости равномерного движения; связь цены, стоимости и количества изделий и т.д.).
План решения.
На основании выявленных отношений между величинами объектов выстраивается последовательность действий - план решения. Особое значение имеет составление плана решения для сложных, составных задач.
Осуществление плана решения включает:
решение задачи - выполнение действий;
запись решения задачи;
выделение способов решения.
Запись решения задачи может осуществляться в виде записи последовательных определенных действий (с пояснениями и без) и в виде выражения (развернутого или сокращенного).
Проверка и оценка решения задачи с точки зрения адекватности плана решения, способа решения, ведущего к результату: рациональность способа, нет ли более простого.
Различные типы задач требуют использования разных методов и приемов решения. Решение задач в 5-6 классах осуществляется в основном тремя способами [1]:
Арифметическим, состоящим в нахождении значений неизвестной величины посредством составления числового выражения (числовой формулы) и подсчета результата;
алгебраическим, при котором составляется уравнение (система уравнений), решение которого основано на свойствах уравнений;
комбинированным, который включает как арифметический, так и алгебраический способы решения.
Арифметические способы решения текстовых задач позволяют развивать умение анализировать задачные ситуации, строить план решения с учетом взаимосвязей между известными и неизвестными величинами (с учетом типа задачи), истолковывать результат каждого действия в рамках условия задачи, проверять правильность решения с помощью составления и решения обратной задачи, то есть формировать и развивать важные общеучебные умения.
Арифметические способы решения текстовых задач приучают детей к первым абстракциям, позволяют воспитывать логическую структуру, могут способствовать созданию благоприятного эмоционального фона обучения, развитию у школьников эстетического чувства применительно к решению задачи (красивое решение) и изучению математики, вызывая интерес сначала к процессу поиска решения задачи, а потом и к изучаемому предмету [3].
При решении арифметическим способом формы записи могут быть:
вопрос с последующим действием;
действие с последующим объяснением;
запись решения с предшествующим пояснением;
числовое решение без всякого текста.
При решении задачи алгебраическим способом существенное значение имеет выбор величины за неизвестное, с помощью которого можно выразить остальные (или часть остальных) величины, входящие в задачу, и установить зависимость между данными задачи, которая даст возможность составить уравнение.
Для многих задач за неизвестное можно принимать величину, которую требуется найти; тогда ответ на вопрос задачи получается без дополнительных вычислений.
При решении сюжетной задачи часто используют сочетание арифметического и алгебраического способов решения. В силу этого форма записи решения каждой части будет разной.
Все сюжетные задачи школьного курса математики 5-6 классов можно сгруппировать следующим образом:
задачи по теме "Натуральные числа" (текстовые задачи на все действия с натуральными числами);
задачи по теме "Рациональные числа" (текстовые задачи на все действия с рациональными числами, на нахождение дроби от числа, на нахождение числа по дроби, задачи на совместную работу, задачи на проценты);
задачи на движение;
задачи на прямую и обратную пропорциональную зависимость;
задачи на составление уравнений;
задачи на смеси и сплавы.
При решении сюжетных задач в курсе математики 5-6 классов очень важно соблюдать преемственность преподавания.
Учитель математики должен познакомиться с методикой преподавания учителя начальных классов, знать основные приемы работы этого учителя и продолжать применять их, не сильно отступая от того, чему дети уже научены (составление схем, таблиц, краткой записи условия задачи и т.д.), дополняя, обогащая способы решения задач своими наработками.
Ученики начальной школы все сюжетные задачи делят на задачи:
в одно действие;
в два действия;
в три действия.
Поэтому чаще всего (особенно слабые) решают задачи перебором действий (какое подойдет).
В 5 классе приходится не сильно отступая от начальной школы исправлять и уделять много внимания решению задач на нахождение отношений между числами ("больше на…", "меньше на…", "больше в … раз", "меньше в …раз"). На помощь приходят задания типа:
нарисуй дом, у которого один этаж;
нарисуй дом, у которого на два этажа больше предыдущего;
нарисуй дом, у которого в два раза больше этажей, чем у предыдущего;
нарисуй дом, у которого в три раза меньше этажей, чем у предыдущего.
В результате получается картинка:

Дети справляются с таким заданием легко, но далеко не все правильно. А проверяют они по рисунку, который показывает учитель. Задания подобного рода нужно давать продолжительное время, пока не исчезнут ошибки, но они не обязательны для всех.
Также очень важно детей учить делать прикидку ответа задачи.
Составление краткой записи условия задачи, схем, рисунков и т.д. учащиеся должны сопровождать объяснением и обсуждением в парах, у доски, индивидуально учителю, но ни в коем случае не молча. Проговаривая каждый свой шаг учащиеся лучше осознают условие задачи и находят в нем все больше и больше знакомых им известных ситуаций, особенно, если эта задача состоит из нескольких элементарных задач.
Помогает в решении сложной задачи расчленение ее на более мелкие ситуации. Ученику лучше предлагать вспомогательную ситуацию из его жизни, интересную и понятную. Например, в магазин пошли не кто-то другой, а ты и твой друг или ты догоняешь на велосипеде своего друга и другие.
Никогда не нужно торопить ребенка с решением, если у него возникают трудности. Нужно попытаться помочь ему еще и еще раз. Обязательно похвалить за решенную задачу, даже если он сам в ней верно сделал только один шаг. В таком случае он на следующем уроке будет вдвойне внимателен и сделает верно уже не один шаг, а больше. И может решить ее всю. Для детей, у которых задачи не получаются, учитель должен становиться помощником, другом, соучастником решения проблемы. Нужно заставить ребенка преодолеть страх перед задачами. Он у них вырабатывается в начальной школе, так как содержание задач не всегда соответствует возрасту.
При решении задач по теме "Натуральные числа" дети опираются на знания, полученные в начальной школе, и при правильно построенной методике преподавания в 5-6 классе с сюжетными задачами справляются.
Задачи "на проценты", "на дроби" можно изучать в комплексе:
вместе все три вида задач на проценты;
вместе нахождение дроби от числа и числа по дроби.
Дети учатся находить отличие в формулировке задач, в данных задачи, в вопросе.
В решении также помогает правильно составленная по условию задачи схема, прикидка ответа и соответствие полученного ответа условию задачи. Нужно добиваться, чтобы дети при решении не пропускали ни одного из этих шагов. Тогда успех обеспечен.
Глава 2. Методика работы с сюжетной задачей на конкретных примерах
Задача 1. Расстояние между двумя причалами 35 км. Сколько времени потратит теплоход на путь по реке от одного причала до другого и обратно, если собственная скорость теплохода 17 км/ч, а скорость течения реки - 3 км/ч?
Работа над текстом задачи.
После прочтения текста задачи учащимися, задаются следующие вопросы:
К какому типу задач относится данная задача?
Что движется по реке?
Какие величины рассматриваются при решении задач на движение по реке?
Какие из величин нам известны?
В каком направлении теплоход двигается по реке?
Как находится скорость по течению реки?
Как находится скорость против течения реки?
Какая величина является искомой?
Решалась ли раньше подобная задача?
Перевод текста на математический язык, установление соотношений между данными и вопросом.
Составляются таблицы 1 и 2, при заполнении 2 таблицы задаются вопросы:
Как найти время движения теплохода по течению реки?
Как найти время движения теплохода против течения реки?
Как найти общее время?
Таблица 1
| νсобст., км/ч | νт. р., км/ч |
| 17 | 3 |
Таблица 2
| Движение теплохода | S, км | ν | t |
| По течению реки | 35 | νсобст. + νт. р. | S: νпо теч. |
| Против течения реки | 35 | νсобств. - νт. р. | S: νпр. теч. |
Правильный ответ на первые 2 вопроса позволяют заполнить четвертый столбец таблицы.
План решения.
Находим скорость теплохода по течению реки.
Находим время, которое он потратил на движение по течению реки.
Находим скорость теплохода против течения реки.
находим время, которое он потратил на движение против течения реки.
Находим общее время, которое потратил теплоход на путь по реке от одного причала до другого и обратно.
Решение в тетради учеников должно выглядеть следующим образом:
17 +3 = 20 (км/ч) - скорость теплохода по течению реки.
35: 20 = 1,75 (ч) - время движения теплохода по течению реки.
17 - 3 = 14 (км/ч) - скорость теплохода против течения реки.
35: 14 = 2,5 (ч) - время движения теплохода против течения реки.
1,75 + 2,5 = 4,25 (ч) - время, которое потратил теплоход на путь по реке от одного причала до другого и обратно.
Ответ: 4,25 ч.
По окончанию решения задачи делаем проверку и оценку решения задачи, задавая такие вопросы учащимся:
Нельзя ли указать другие способы решения данной задачи?
Что повторили при решении данной задачи?
Почему рассмотренный способ является рациональным?
Задача 2. Площадь участка поля 80 га, первый тракторист вспахал 40% этого участка, а второй 60% оставшейся части. Кто из них вспахал больше и на сколько га?
Работа над текстом задачи.
Интерес к решению задачи поднимется если разыграть ее в классе.
Вопросы на понимание содержания:
О чем говориться в задаче?
Что известно в задаче?
Можно ли сделать предположение кто вспахал больше и если отвечаем да, то сделайте его?
Известна ли площадь поля?
Что такое 1%? Как находиться?
За сколько процентов принимаем все поле?
Больше или меньше половины вспахал 1 тракторист?
Можем ли ответить на предыдущий вопрос про второго тракториста?
Как находиться оставшаяся часть поля?
Что будем сравнивать, отвечая на вопрос, кто из них вспахал больше?
Какой способ выберем для решения задачи?
Перевод текста на математический язык, установление соотношений между данными и вопросом.
Все поле изображаем
Это 100%. Разделим его на 2 части.
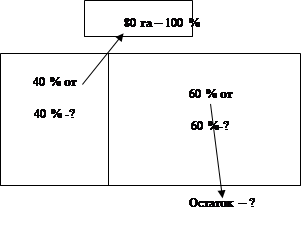
Первый тракторист вспахал 40% от всего поля. Сколько будут это в га обозначим знаком вопроса.
Вторая часть прямоугольника это остаток. Обязательно под ней написать слово остаток и поставить знак вопроса. Во второй части прямоугольника записываем 60% к слову остаток.
Сколько вспахал 2 тракторист обозначим знаком вопроса.
План решения.
Найти сколько вспахал первый тракторист.
Найти сколько осталось вспахать после первого тракториста.
Найти сколько вспахал второй тракторист.
Найти на сколько один тракторист вспахал больше другого?
Решение в тетради учеников должно выглядеть следующим образом:
80: 100 * 40 = 32 (га) вспахал 1 тракторист
80 - 32 = 48 (га) остаток
48: 100 * 60 = 28,8 (га) вспахал 2 тракторист
32 - 28,8 = 3,2 (га) на столько га 1 тракторист вспахал больше 2 тракториста
Ответ: на 32 га
По окончанию решения задачи делаем проверку и оценку решения задачи, задавая такие вопросы учащимся:
Понравилась ли задача?
Кто оказался прав в предположении?
Есть ли другой способ решения?
Придумайте 1-2 похожих на эту задачу, например, про работу на пришкольном участке, в летнем лагере.
Задача 3. Через 2 крана бак наполняется за 9 минут. Если бы бал открыт только первый кран, то бак наполнился бы за 36 минут. За сколько минут наполнился бы бак через один второй кран?
Работа над текстом задачи.
Задаем вопросы:
Что происходит в задаче?
Известно ли время за которое наполняется бак с помощью двух кранов?
С помощью первого крана?
С помощью второго крана?
Через второй кран бак будет наполняться больше или меньше девяти минут?
Какая часть бака наполняется за 1 минуту 2 кранами вместе?
Какая часть бака наполняется 1 краном за 1минуту?
Перевод текста на математический язык, установление соотношений между данными и вопросом.
Составляем таблицу:
| Время заполнения бака | Часть бака наполняется за 1 мин. | |
| 1 кран | 36 | ? |
| 2 кран | ? | ? |
| вместе | 9 | ? |
План решения.
Какая часть бака наполняется за 1 минуту 2 кранами вместе?
Какая часть бака наполняется за 1 минуту первым краном?
Какая часть бака наполняется за 1 минуту вторым краном?
За какое время наполняется бак через один 2 кран?
Решение в тетради учеников должно выглядеть следующим образом:
1: 9 = ![]() часть бака наполняется за 1 мин 2 кранами вместе
часть бака наполняется за 1 мин 2 кранами вместе
1: 36 = ![]() часть бака наполняется за 1 мин первым краном
часть бака наполняется за 1 мин первым краном
![]() -
- ![]() =
= ![]() =
= ![]() часть бака наполняется за 1 мин вторым краном
часть бака наполняется за 1 мин вторым краном
1: ![]() = 12 (мин) наполняется бак одним вторым краном
= 12 (мин) наполняется бак одним вторым краном
Ответ: 12 мин
По окончанию решения задачи делаем проверку и оценку решения задачи, задавая такие вопросы учащимся:
Что показалось трудным в решении задачи?
Есть ли другие способы решения?
Придумать похожую задачу про заполнение бассейна.
Задача 4. Тесто для вареников содержит 16 частей творога, 2 части муки, 1 часть масла, 3 части сметаны, 3 части сахара. Определите мессу каждого продукта в отдельности для приготовления 1 кг теста.
Работа над текстом задачи.
Похожие работы
... способом аналитико – синтетический метод применяется на тех – же решениях. Единственное различие состоит в том , что на этапе поиска решения применяется анализ в нисходящей форме. Методика обучения решения технических задач. Математические задачи, в которых есть хотя бы один объект, являющийся реальным предметом, принято называть текстовыми (сюжетными, практическими, арифметическими и т.д) ...
... выдвинутой гипотезы на базе школы № 24 был проведен психолого-педагогический эксперимент, цель которого: изучить специфические особенности и пути усовершенствования процесса обучения школьников решению составных задач. Задачи экспериментальной части исследования: - Рассмотрев известные, но мало применяемые на практике способы работы над составной задачей, включить их в практическую работу с ...
... и перенести полученные знания на практику. Глава 2. Работа учителя по развитию логического мышления на уроках математики 2.1 Опытно-экспериментальная работа и анализ ее результатов Опытно-экспериментальное исследование по выявлению уровня развития логического мышления школьников при решении текстовых задач проводилось на базе МОУ «Средняя общеобразовательная школа № 10» г. Кунгура в ...
... развитие логического мышления учащихся является одной из основных целей курса геометрии. При изучении геометрии развитие логического мышления учащихся осуществляется в процессе формирования понятий, доказательства теорем, решения задач. При изучении геометрических построений, прежде всего, приходится преодолевать трудности логического порядка. В условиях школы для преодоления этих трудностей ...





0 комментариев