Ниже перечислены разные события. Укажите противоположные им события

1. Ниже перечислены разные события. Укажите противоположные им события.

а) Мою новую соседку по парте зовут или Таня, или Аня.

б) Из пяти выстрелов в цель попали хотя бы два.

в) На контрольной работе я не решил, как минимум, три задачи из пяти.

2. Назовите событие, для которого противоположным является такое событие:

а) на контрольной работе больше половины класса получили пятёрки;

б) все семь пулек в тире у меня попали мимо цели;

в) в нашем классе все умные и красивые;

г) в кошельке у меня есть три рубля одной монетой, или три доллара одной бумажкой.

Рассматривая события как множества, можно определить действия над событиями. (Введение понятий суммы и произведения событий позволяет подготовить действия над вероятностями).

a)         Объединение событий или сумма событий - AÈB или А+В - событие, содержащее все элементы А и В.

Пример 1.

Испытание: бросаем игральную кость.

Событие А: выпало четное число очков.

Событие B: выпало число очков меньше, чем 4.

Событие A+B: выпало 1, 2, 3, 4 или 6 очков.

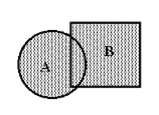
Пример 2.

Событие А: круг.

Событие B: квадрат.

Событие A+B: заштриховано.

b)         Пересечение событий или произведение событий - AÇB или АВ - событие, содержащее только общие элементы А и В.

Пример 3.

Испытание: бросаем игральную кость.

Событие А: выпало четное число очков.

Событие B: выпало число очков меньше, чем 4.

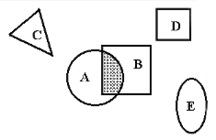Событие AB: выпало 2 очка.

Пример 4.

Событие А: круг.

Событие B: квадрат.

Событие AB: заштриховано.

Какими являются события C, D, E?

Задачи:

1.         Событие А – «попадание в мишень первым выстрелом», событие В – «попадание в мишень вторым выстрелом». В чем состоит событие А+В?

2.         Событие А – «ученик учится без троек», событие В – «ученик учится без двоек», событие С – «ученик не отличник». Сформулируйте: А+В+С.

3.         Событие А – «лотерейный выигрыш 10 руб.», событие В – «лотерейный выигрыш 20 руб.», событие С – «лотерейный выигрыш 30 руб.», событие D – «лотерейный выигрыш 40 руб.». В чем состоит событие А+В+С+D?

4.         Событие А – «появление нечетного числа очков при бросании игральной кости», событие В – «появление 3 очков при бросании игральной кости», событие С – «появление 5 очков при бросании игральной кости». В чем состоят события АВС, АВ, АС, ВС?

5.         Проводятся две лотереи. Если событие А₁ – «выигрыш по билету первой лотереи» и событие А₂ – «выигрыш по билету второй лотереи», то что означают события: А₁А₂+А₂, А₁+А₂+А₁А₂?

6.         Известно, что события А и В произошли, а событие С не наступило. Определите, наступили ли следующие события: А+ВС, (А+В)С, АВ+С, АВС.

7.         Турист из пункта А в пункт В может попасть двумя дорогами. обозначим события: А₁ – «он пошел первой дорогой», А₂ – «он пошел второй дорогой».

Из пункта В в пункт С ведут три дороги. Обозначим события: В₁ – «он пошел первой дорогой», В₂ – «он пошел второй дорогой», В₃ – «он пошел третьей дорогой».

Применяя понятия суммы и произведения, а также противоположного события, постройте события, состоящие в том, что:

-          от А до В он выбрал дорогу наугад, а от В до С пошел третьей дорогой;

-          от А до В он пошел первой дорогой, а от В до С – дорогой, выбранной наугад;

-          от А до В он пошел не первой дорогой, а от В до С – не третьей;

-          он дошел от А до С.

Занятие №3. Эксперименты и их исходы.

Первый шаг на пути ознакомления учащихся с понятием вероятность состоит в длительном экспериментировании, то есть в многочисленных манипуляциях с разнородными предметами (игральными костями, волчками, монетами, шарами и прочими).

Для проведения экспериментов учащихся лучше разбить на группы по 2-3 человека, один из которых будет фиксировать результаты эксперимента, а остальные проводить его.

Могут быть предложены следующие задания-эксперименты:

Задание №1. 100 раз подбросить монету и зафиксировать количество выпадений «орла» и «решки».

Задание №2. 100 раз подбросить кнопку и зафиксировать количество раз, когда кнопка упала острием вниз и количество раз, когда кнопка упала острием вверх.

Задание №3. Выберите какой-нибудь текст, содержащий 150 слов. Подсчитайте число слов, составленных из 6 букв.

Задание №4. Выберите 7 строк произвольного текста. Подсчитайте, сколько раз встречаются в тексте буквы о, е, а, ю.

Задание №5. 100 раз подбросить игральную кость и зафиксировать количество выпадений 6.

После проведения экспериментов целесообразно ввести понятия эксперимента и его исхода. Четкое определение и разграничение при проведении реальных физических экспериментов таких понятий, как исход эксперимента и событие, возможное в эксперименте, в дальнейшем поможет избежать многих трудностей при введении понятия вероятности случайного события.

Занятие №4. Классическое определение вероятности.

Вероятность – одно из основных понятий теории вероятностей. Существует несколько определений этого понятия. Приведем определение, которое называют классическим. Далее укажем слабые стороны этого определения и приведем другие определения, позволяющие преодолеть недостатки классического определения.

Рассмотрим пример. Пусть в урне содержится 6 одинаковых, тщательно перемешанных шаров, причем 2 из них – красные, 3 – синие и 1 – белый. Очевидно, возможность вынуть наудачу из урны цветной шар больше, чем возможность извлечь белый шар. Можно ли охарактеризовать эту возможность числом? Оказывается, можно. Это число и называют вероятностью события. Таким образом, вероятность есть число, характеризующая степень возможности появления события.

Поставим перед собой задачу дать количественную оценку возможности того, что взяты наудачу шар цветной. Появление цветного шара будем рассматривать в качестве события А. Каждый из возможных результатов испытания (испытание состоит в извлечении шара из урны) назовем элементарным исходом (элементарным событием). Легко видеть, что эти исходы образуют полную группу попарно несовместных событий (обязательно появится только один шар) и они равновозможны (шар вынимают наудачу, шары одинаковые и тщательно перемешаны).

Те элементарные исходы, в которых интересующее нас событие наступает, назовем благоприятствующими этому событию.

Необходимо пояснить учащимся различие между событием и элементарным событием.

Отношение числа благоприятствующих событию А элементарных исходов к их общему числу, называют вероятностью события А и обозначают Р(А). В рассматриваемом примере всего элементарных исходов 6; из них 5 благоприятствуют событию А. Следовательно, вероятность того, что взятый шар окажется цветным, равна Р(А)=5/6.Это число и дает ту количественную оценку степени возможности появления цветного шара, которую мы хотели найти. Дадим теперь определение вероятности.

Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.

, где m - число элементарных исходов, благоприятствующих А; n – число всех возможных элементарных исходов испытания.

m

P(A)=

n

m

n

Полезно формуле вероятности события придать наглядную иллюстрацию.
Из определения вероятности вытекают следующие ее свойства:

Свойство 1. Вероятность достоверного события равна единице.

Свойство 2. Вероятность невозможного события равна нулю.

Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Доказательства данных свойств могут быть предложены учащимся в качестве домашнего задания.

Задачи:

1.         Для новогодней лотереи отпечатали 1500 билетов, из которых 120 выигрышных. Какова вероятность того, что купленный билет окажется выигрышным?

2.         Для экзамена подготовили билеты с номерами от 1 до 25. какова вероятность того, что взятый наугад учеником билет имеет: 1) однозначный номер; 2) двузначный номер?

3.         Ученик при подготовке к экзамену не успел выучить один из тех 25 билетов, которые будут предложены на экзамене. Какова вероятность того, что ученику достанется на экзамене выученный билет?

4.         Женя купил 2 лотерейных билета, и один из них оказался выигрышным. Можно ли утверждать, что вероятность выигрыша в лотереи ?

5.         Для школьного новогоднего вечера напечатали 125 пронумерованных пригласительных билетов, между которыми предполагается разыграть главный приз. Какова вероятность, что номер счастливчика будет оканчиваться: а) на тройку; б) на девятку? в) Вова получил пригласительный билет с номером 33, а Таня – 99. Верно ли, что у Вовы больше шансов получить главный приз?

6.         Два друга живут в одном доме, а учатся в разных классах. Уроки в школе заканчиваются в интервале от 13 до 14 часов. После занятий они договариваются ждать друг друга на автобусной остановке в течение 20 минут. Сколько приблизительно раз за год им удаётся поехать домой вместе, если в году 200 учебных дней?

Занятие №5. Решение вероятностных задач с помощью формул комбинаторики.

При изучении этой темы надо, чтобы учащиеся отчетливо представляли себе роль сочетаний, размещений и перестановок в различных вероятностных задачах и научились по формулировкам задач определять, какой из видов соединений будет использован при решении той или иной задачи. Здесь можно руководствоваться следующим: если множество исходов составляют всевозможные комбинации из n элементов по k, то в задаче будут фигурировать сочетания; если же всевозможные комбинации из n элементов по n, то в задачах идет речь о перестановках; размещения будут тогда, когда речь идет о порядке элементов в рассматриваемых комбинациях.

Задачи:

1.         Набирая номер телефона, абонент забыл последние две цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.

2.         В классе 30 учащихся. Из них 12 мальчиков, остальные девочки. Известно, что к доске должны быть вызваны двое учащихся. Какова вероятность, что это девочки?

3.         Набирая номер телефона, состоящий из 7 цифр, Антон забыл, в какой последовательности идут три последние цифры. Помня лишь, что это цифры 1, 5 и 9, он набрал первые 4 цифры, которые знал, и наугад комбинацию из цифр 1, 5 и 9. какова вероятность того, что Антон набрал верный номер?

4.         В пачке находятся одинаковые по размеру 7 тетрадей в линейку и 5 в клетку. Из пачки наугад берут 3 тетради. Какова вероятность того, что все 3 тетради окажутся в клетку?

5.         Четыре билета на ёлку распределили по жребию между 15 мальчиками и 12 девочками. Какова вероятность того, что билеты достанутся 2 мальчикам и 2 девочкам?

6.         На полке 12 книг, из которых 4 – это учебники. С полки наугад снимают 6 книг. Какова вероятность того, что 3 из них окажутся учебниками?

Занятие №6. Статистическая вероятность.

Классическое определение не требует, чтобы испытание обязательно проводилось в действительности: теоретическим способом определяются все равновозможные и благоприятствующие событию исходы. Такое определение предполагает, что число элементарных исходов испытания конечно и выражается конкретным числом. Однако на практике – при изучении случайных явлений в естествознании, экономике, медицине, производстве – часто встречаются испытания, у которых число возможных исходов необозримо велико. А в ряде случаев до проведения реальных испытаний трудно или не возможно установить равновозможность исходов испытания. Поэтому, наряду с классическим, на практике используют и так называемое статистическое определение вероятности. Для знакомства с ним требуется ввести понятие относительной частоты.

Относительной частотой события A называют отношение числа испытаний m, в которых событие появилось, к общему числу фактически произведенных испытаний n.

Таким образом, вероятность вычисляют до опыта, а относительную частоту после опыта.

Длительные наблюдения показали, что если в одинаковых условиях производят опыты, в каждом из которых число испытаний достаточно велико, то относительная частота обнаруживает свойство устойчивости. Это свойство состоит в том, что в различных опытах относительная частота изменяется мало, колеблясь около некоторого постоянного числа.

Например, по данным шведской статистики, относительная частота рождения девочек в 1935 г по месяцам характеризуется следующими числами: 0,486; 0,489; 0,490;0,471;0,478;0,482;0,462;0,484;0,485;0,491;0,482;0,473. относительная частота колеблется около числа 0,482, которое можно принять за приближенное значение вероятности рождения девочек

Таким образом, в качестве статистической вероятности события принимают относительную частоту или число, близкое к ней.

Свойства вероятности, вытекающие из классического определения, сохраняются и при статистическом определении вероятности. Назовите их.

Задачи:

1.         Во время тренировки в стрельбе по цели было сделано 30 выстрелов и зарегистрировано 26 попаданий. Какова относительная частота попадания по цели в данной серии выстрелов?

2.         Отдел технического контроля обнаружил пять бракованных книг в партии из случайно отобранных 100 книг. Найти относительную частоту появления бракованных книг.

3.         Дано распределение дней рождения старшеклассников (учащихся 9-11 классов) по месяцам и дням недели

	пн	вт	ср	чт	пт	сб	вс
январь	0	1	3	4	0	0	1
февраль	2	4	1	2	3	0	2
март	2	2	0	2	4	2	0
апрель	3	2	5	8	0	3	2
май	4	0	2	1	1	1	2
июнь	4	2	2	1	3	2	0
июль	0	1	4	2	1	2	0
август	1	2	4	4	2	0	1
сентябрь	0	1	2	1	2	3	5
октябрь	1	2	0	0	2	1	0
ноябрь	0	2	4	1	1	5	1
декабрь	2	2	3	2	0	2	2

Найдите относительные частоты событий:

А = {старшеклассник родился в майское воскресенье};

В ={старшеклассник родился в зимний четверг};

С = {старшеклассник родился в понедельник};

D = {старшеклассник родился весной}.

Занятие №7. Геометрическая вероятность.

Геометрическая вероятность – это своеобразный аналог формулы классического определения вероятности события: отношение двух натуральных чисел (количество благоприятных исходов к количеству всевозможных исходов) в формуле классического определения вероятности событий заменяется отношением мер (длин, площадей, объемов) геометрических множеств, где оба множества (в общем случае) представляют собой бесконечные множества исходов. Тем самым достигается возможность найти вероятность и в случае бесконечного множества исходов. В этом – конечное и бесконечное множества исходов – и заключается основное различие между классическим определением вероятности события и геометрическим.

Рассмотрение геометрической вероятности развивает у учащихся пространство воображения и способствует формированию умений переводить исходную вероятностную ситуацию на геометрический язык.

Геометрические вероятности можно дать в ознакомительном порядке, разобрав для этого ряд задач.

Задачи:

1.         На отрезке L длины 20 см помещен меньший отрезок l длины 10 см. найти вероятность того, что точка, наудачу поставленная на большой отрезок, попадет и на меньший отрезок. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения.

2.         Внутри квадрата со стороной 10 см выделен круг радиусом 2 см. случайным образом внутри квадрата отмечается точка. Какова вероятность того, что она попадет в выделенный круг?

3.         На плоскости начерчены две концентрические окружности, радиусы которых 5 и 10 см соответственно. Найти вероятность того, что точка, брошенная наудачу в большой круг, попадет также и в кольцо, образованное построенными окружностями. Предполагается, что вероятность попадания точки в плоскую фигуру пропорциональна площади этой фигуры и не зависит от ее расположения.

4.         Перед окопами вдоль прямой линии через каждые 10 м установлены противотанковые мины. Перпендикулярно этой линии движется танк, ширина которого 3 м. Какова вероятность того, что танк пересечет линию установки мин невредимым, то есть, что мина не взорвется?

Занятие №8. Теорема сложения вероятностей.

Из четырех теорем о сложении вероятностей (для двух несовместных событий, для n несовместных событий (обобщение), для событий, образующих полную группу и для противоположных событий) практический интерес для слушателей курса представляют лишь две теоремы: первая и третья. Обе они часто используются при решении вероятностных задач, и поэтому их следует подробно с доказательством рассмотреть на занятии. Теорему о противоположных событиях (как частный случай третьей теоремы) можно поручить рассказать одному из учащихся.

Теорема 1. Пусть события А и В – несовместные, причем вероятности этих событий известны. Тогда вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Р(А+В)=Р(А)+Р(В).

Доказательство. Введем обозначения: n – общее число возможных элементарных исходов испытания; m₁ – общее число исходов, благоприятствующих событию А; m₂ – общее число исходов, благоприятствующих событию В.

Число элементарных исходов, благоприятствующих наступлению либо события А, либо события В, равно m₁+m₂. Следовательно,

Р(А+В)=.

Приняв во внимание, что  и , окончательно получим

Р(А+В)=Р(А)+Р(В).

Теорема 2. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Р(А₁+А₂+…+А_n)=Р(А₁)+Р(А₂)+…+Р(А_n).

Теорема 3. Сумма вероятностей событий А₁, А₂, …, А_n, образующих полную группу, равна 1:

Р(А₁)+Р(А₂)+…+Р(А_n)=1.

Доказательство. Так как появление одного из событий полной группы достоверно, а вероятность достоверного события равна единице, то

Р(А₁+А₂+…+А_n)=1. (*)

Любые два события полной группы несовместны, поэтому можно применить теорему сложения:

Р(А₁+А₂+…+А_n)=Р(А₁)+Р(А₂)+…+Р(А_n). (**)

Сравнивая (*) и (**), получим

Р(А₁)+Р(А₂)+…+Р(А_n)=1.

Теорема 4. Сумма вероятностей противоположных событий равна 1:

Р(А)+Р()=1.

Задачи: