Навигация
Шаталов, В.Ф. Методические рекомендации для работы с опорными сигналами по тригонометрии [Текст] / Шаталов В.Ф. - Москва: Новая школа, 1993
22. Шаталов, В.Ф. Методические рекомендации для работы с опорными сигналами по тригонометрии [Текст] / Шаталов В.Ф. - Москва: Новая школа, 1993.
23. Шенфельд, Х. Что общего между заходом солнца и функцией y=sin х [Текст] /Шенфельд Х. // Математика в школе. 1993-№2- с.75-77.
Приложение
Факультатив «Тригонометрия помогает алгебре».
Известно, что «тот или иной материал усваивается школьниками не тогда, когда этот материал является целью обучения, а тогда, когда он становится средством для решения других задач»[10]. Поэтому целесообразно показать учащимся то, как можно применять свойства тригонометрических функций и тригонометрические тождества при решении, например, алгебраических задач.
Цели:
1) Провести межпредметные связи между тригонометрией и алгеброй.
2) Способствовать формированию умений решать некоторые виды уравнений алгебры с помощью тригонометрических подстановок.
Место изучения.
Этот факультатив желательно проводить после того, как изучены все разделы тригонометрии.
Ход факультатива:
Учащимся предлагается попробовать решить уравнение ![]() самостоятельно. Попробовав выполнить стандартное возведение в квадрат обеих частей, учащиеся натыкаются на уравнение 6-ой степени, решение которых в школьном курсе не рассматривается. Обратив внимание учащихся, на то, что областью допустимых значений переменной данного уравнения является отрезок [-1;1], учитель предлагает вспомнить изученные функции, областью значений которых является данный отрезок. После чего делается вывод: если из условия задачи следует, что допустимые значения переменной x определяются неравенством |x|≤1, то удобны замены х=sinα, α
самостоятельно. Попробовав выполнить стандартное возведение в квадрат обеих частей, учащиеся натыкаются на уравнение 6-ой степени, решение которых в школьном курсе не рассматривается. Обратив внимание учащихся, на то, что областью допустимых значений переменной данного уравнения является отрезок [-1;1], учитель предлагает вспомнить изученные функции, областью значений которых является данный отрезок. После чего делается вывод: если из условия задачи следует, что допустимые значения переменной x определяются неравенством |x|≤1, то удобны замены х=sinα, α![]() , или х=cosα,
α
, или х=cosα,
α![]() , причем какую из них выбрать, зависит от конкретной задачи.
, причем какую из них выбрать, зависит от конкретной задачи.
Учащиеся совместно с учителем прорешивают данное уравнение.
«Поскольку функция 4х3-3х существует при любых значениях х, найдем область определения функции f(x)= ![]() : 1- х2 ≥0, значит х
: 1- х2 ≥0, значит х![]() . Введем замену х=cosα. Нас интересуют все значения этой функции. Выберем для удобства любой отрезок, на котором функция косинус принимает все свои значения, например отрезок
. Введем замену х=cosα. Нас интересуют все значения этой функции. Выберем для удобства любой отрезок, на котором функция косинус принимает все свои значения, например отрезок ![]() .
.
Подставим х=cosα в уравнение, получим ![]()
Так как α![]() , то sinα ≥0 и можно опустить модуль:
, то sinα ≥0 и можно опустить модуль:
![]()
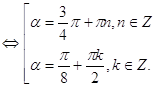
Условию α![]() удовлетворяют три значения α1=
удовлетворяют три значения α1=![]() , α2=
, α2=![]() ,α3=
,α3=![]() .
.
x1=cos α1=cos![]() =
=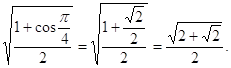 ,
,
x2=cos α2=cos![]() =-sin
=-sin![]() =
= 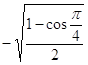 =
=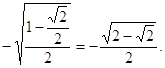
x3= cos α3=cos ![]() =-cos
=-cos![]() =
=![]() .
.
Ответ: x1=![]() , x2=
, x2=![]() , x3=
, x3=![]() .
.
Пример 2. Сколько корней на отрезке [0;1] имеет уравнение
![]()
При отсутствии лишнего времени решение лучше вынести в качестве домашнего задания. Если уровень подготовки класса не очень высок, то учитель может сделать подсказку «Замена х=cosα, α![]() ставит в соответствие каждому значению х на [0;1] ровно одно значение α
ставит в соответствие каждому значению х на [0;1] ровно одно значение α![]() . Значит, число решений исходного уравнения на [0;1] равно числу решений соответствующего уравнения на
. Значит, число решений исходного уравнения на [0;1] равно числу решений соответствующего уравнения на ![]() , причем так как х¹0 и х¹1, то можно взять α
, причем так как х¹0 и х¹1, то можно взять α![]() ». Уравнение примет вид
». Уравнение примет вид
![]()
![]()
![]()
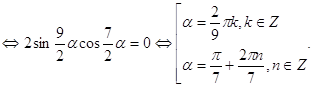
Условию α![]() удовлетворяют четыре значения α1=
удовлетворяют четыре значения α1=![]() , α2=
, α2=![]() , α3=
, α3=![]() , α4=
, α4=![]() .
.
Ответ: уравнение на отрезке [0;1] имеет ровно четыре корня.
Пример 3. Решить систему уравнений
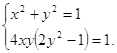
Внимательно посмотрев на первое уравнение системы, учащиеся сами (или с помощью учителя) замечают, что оно очень похоже на основное тригонометрическое тождество и делают вывод: если в задаче встречается равенство х2+y2=1, то часто бывает полезно сделать замену х= sinα, y= cosα, α![]() , так как числа, сумма квадратов которых равна 1, это синус и косинус одного и того же числа. Дальнейшее решение системы не вызывает затруднений и может быть произведено учащимися самостоятельно.
, так как числа, сумма квадратов которых равна 1, это синус и косинус одного и того же числа. Дальнейшее решение системы не вызывает затруднений и может быть произведено учащимися самостоятельно.
Пусть х= sinα, y= cosα, α![]() Второе уравнение системы примет вид
Второе уравнение системы примет вид
![]()
Условию α![]() удовлетворяют четыре значения α1=
удовлетворяют четыре значения α1=![]() , α2=
, α2=![]() , α3=
, α3=![]() , α4=
, α4=![]() .
.
х1=![]() y1=
y1=![]()
х2=![]() y2=
y2=![]()
х3=![]() y3=
y3=![]()
х4=![]() y4=
y4=![]()
Ответ: х= ![]() , y=
, y= ![]() ; x=
; x= ![]() , y=
, y= ![]() ; x=
; x= ![]() ,
,
y= ![]() ; x=
; x= ![]() , y=
, y= ![]() .
.
В качестве домашнего задания учащимся можно предложить решить задачу:
Числа a, b, c, d таковы, что a2+b2=1, c2+d2=1, ac+bd=0. Чему равно ab+cd?
Решение может выглядеть следующим образом. «Пусть а= sinα, b= cosα, α
![]()
Преобразуем выражение ab+cd:
![]()
Так как cos(α- β)=0, то sin(α +β)*cos(α - β)=0, a значит ab+cd=0.
Ответ: ab+cd=0»
После этого учитель подводит учащихся к вопросу: «Можно ли применять тригонометрические подстановки для решения уравнений, в область допустимых значений которых входят все действительные числа?»
Можно, но в случаях, когда переменная может принимать различные значения, используются замены x=tgα, α![]() и x=ctgα, α
и x=ctgα, α![]() .
.
Пример 5. Доказать, что при любых действительных х и у
![]() .
.
Замечание. Желательно обсудить с учащимися лишь необходимую замену. Все остальное они в силах проделать самостоятельно.
Положим ![]() , где
, где ![]() . Тогда
. Тогда
![]()
![]()
Так как все значения выражения
![]() лежат в промежутке [-1/2;1/2], следовательно, и все значения исходного выражения лежат в этом же промежутке. Что и требовалось доказать.
лежат в промежутке [-1/2;1/2], следовательно, и все значения исходного выражения лежат в этом же промежутке. Что и требовалось доказать.
* более подробно эти вопросы изложены в параграфе 3
1) Напомним, что обучение по учебнику [2] предполагает изучение тригонометрических уравнений в конце 10-го класса, а изучение тригонометрических функций только в начале 11го.
Похожие работы
... сформулированной гипотезы необходимо было решить следующие задачи: 1. Выявить роль тригонометрических уравнений и неравенств при обучении математике; 2. Разработать методику формирования умений решать тригонометрические уравнения и неравенства, направленную на развитие тригонометрических представлений; 3. Экспериментально проверить эффективность разработанной методики. Для решения ...
... детальный разбор этого материала при активной работе учащихся. Тщательно рассматриваются все определения, прорешиваются примеры – идет усвоение нового материала. 2.2 Методика введения показательной функции Изучение темы «Показательная функция» в курсе алгебры и начала анализа предусматривает знакомство учащихся с вопросами: Обобщение понятия о степени; понятие о степени с иррациональным ...
... (вопросы а) и в)). Понятие функции, в системе формирования которого должны присутствовать такие задания, сразу выступает в курсе математики как определённая математическая модель, что и является мотивировкой для его углублённого изучения. Методика введения понятий: функции, аргумента, области определения. Не смотря на чрезвычайно большой объем, широту и сложность понятия функции, его ...
... функций, имеющих одинаковое основание, симметричны относительно прямой (рис. 3). Рис. 3 Глава 3. Тождественные преобразования показательных и логарифмических выражений на практике. Задание 1. Вычислите: 1.1) ; 1.2) ; 1.3) ; 1.4) ; 1.5) . Решение: 1.1) ; 1.2) ; 1.3) ; 1.4) ; 1.5) . Ответ: ; ; ; ; . Задание 2. Упростите выражения: 2.1) ; ...








0 комментариев