Аналіз існуючих програмно-педагогічних засобів з теми дослідження

1.4 Аналіз існуючих програмно-педагогічних засобів з теми дослідження

 

Національною доктриною розвитку освіти в Україні у XXI столітті визначено, що пріоритетом розвитку освіти є впровадження сучасних інформаційних технологій, що забезпечують подальше вдосконалення навчально-виховного процесу, доступність та ефективність освіти, підготовку молодого покоління до життєдіяльності в сучасному комп’ютеризованому суспільстві [41].

Упровадження сучасних інформаційних технологій навчання розкриває широкі можливості щодо суттєвого зменшення навчального навантаження і, водночас, інтенсифікації навчального процесу, надання навчально-пізнавальній діяльності творчого, дослідницького спрямування.

Хоча на сьогоднішній день створено значну кількість навчальних програм, але вони мають певні недоліки. Це стосується і програм з курсу фізики.

Ми проаналізували деякі існуючі програми з фізики. Більшість програм російського видавництва («Открытая физика», «Физикус», «Репетитор по физике»), отже, зорієнтовані на російські стандарти фізичної освіти, зрозуміло, що і текстовий матеріал подається російською мовою. В багатьох програмах спостерігаються помилки, невірно подаються означення понять, помилки в позначеннях фізичних величин на графіках і малюнках, синтаксичні і граматичні помилки. Наявні комп’ютерні програми і програмно-методичні комплекси не забезпечують на належному рівні навчально-виховний процес з фізики. Тому проблема розробки комп’ютерних програм навчального призначення залишається відкритою.

Серед програм вітчизняного виробництва слід відзначити програмно-методичні комплекси «Фізика-7» «Фізика-8» «Фізика-9», створені групою спеціалістів Інституту педагогіки АПН України й корпорацією «Квазар Мікро» [2, 3].

Більш детальніше проаналізуємо деякі із вище згаданих програмних комплексів щодо того, як в них подається матеріал з теми нашого дослідження.

«Физикус» – це російськомовна навчальна програма, розроблена фірмою «Медиахауз». Складається вона із двох дисків і розроблена у вигляді гри, під час якої користувач заходить у будиночок, де повинен набути певних знань. У цій програмі приділена увага п’яти основним розділам фізики: оптиці, механіці, акустиці, електриці, термодинаміці. По кожному із них створена певна кількість керованих динамічних моделей дослідів, експериментів та будови і принципу дії деяких приладів. Позитивною стороною даної програми є її простота у використанні, доступність для розуміння, хороша графіка та динамічність моделей. Але вона має і певні недоліки. В першу чергу це те, що вона охоплює далеко не весь матеріал шкільної програми, а лише деякі його окремі аспекти.

Що стосується геометричної оптики, то тут розглянуто лише наступні моменти: тінь, сонячне та місячне затемнення, відбивання та поглинання променів світла, плоске дзеркало, заломлення, повне відбивання, збиральна та розсіювальна лінза, будова ока та дефекти зору, лупа, мікроскоп та телескоп. Звичайно ж для вивчення геометричної оптики цього недостатньо, хоча при вивченні деяких тем ця програма може дуже допомогти.

«1С: Репетитор по физике» Що стосується цього програмного комплексу, то він охоплює значно більший обсяг матеріалу, ніж «Физикус». За своїм основним призначання він є помічником при самостійному вивченні чи повторенні навчального матеріалу (наприклад, при підготовці до вступу у вуз). У ньому, наприклад, є такі корисні та цікаві складові, як словник, біографії вчених, технічний калькулятор тощо. Також важливою особливістю програми є те, що вона автоматично реєструє, скільки часу і по якій темі працював учень, а також кількість правильно та неправильно розв’язаних задач. Також дана програма містить цікаві пізнавальні відеофрагменти та динамічні моделі, які, на нашу думку, значно підвищують рівень засвоєних знань. Однак, ця програма охоплює далеко не весь шкільний курс фізики.

Отже, враховуючи вище згадане, можна зробити висновок, що питання створення програмних навчальних комплексів залишається відкритим та актуальним і на сьогоднішній день.

2. Методичні аспекти поєднання традиційних та інформаційних технологій при вивченні геометричної оптики

 

2.1 Аналіз методичної системи вивчення геометричної оптики в загальноосвітній школі

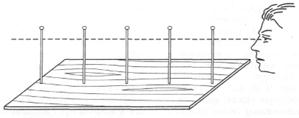
Серед основних властивостей світла найбільш наочною, підтвердженою широким життєвим досвідом є властивість прямолінійно поширюватися в однорідному ізотропному середовищі. Лінія, вздовж якої поширюється енергія світла, називається світловим променем. Отже, промінь – суто геометричний образ. Саме тому, що промінь відображає тільки одну властивість світла, це поняття можна використовувати лише в певних межах. Здавалося б, що промінь можна утворити на досліді, якщо на шляху світла поставити діафрагму з невеликим отвором. Але насправді це не зовсім так. Якщо отвір діафрагми широкий, на екрані утворюється розмита пляма, за формою подібна до діафрагми. Зменшуючи отвір діафрагми, побачимо, що тіньове зображення отвору переходить у чітке зображення джерела світла. Чіткість зображення зростає із зменшенням отвору. Проте це відбувається лише до певної межі, після чого дальше зменшення отвору діафрагми призводить до розмивання зображення. Нарешті, коли отвір дуже малий, весь екран буде повністю освітлений.

Пучок світла від джерела, що обмежується отвором діафрагми, можна вважати наближеною моделлю променя. Зменшуючи розмір отвору діафрагми, утворюємо все вужчий пучок. Проте ми не матимемо змоги створити нескінченно вузький світловий пучок – промінь. Справді, дослід показує, що дальше зменшення розміру діафрагми не тільки не приводить до зменшення перерізу пучка, а, навпаки, веде до його розширення. Тут уже проявляються хвильові властивості світла. Тому обмежимося виділенням вузьких світлових пучків і замінимо їх потім осьовими лініями, які й називатимемо променями світла.

Поняття про промінь світла дає змогу вивчити й осмислити цілий ряд оптичних явищ і законів, пояснити будову і призначення багатьох оптичних приладів. Розділ оптики, що ґрунтується на понятті про промінь, називається променевою або геометричною оптикою. Основне завдання променевої оптики – вивчення будови та дії оптичних приладів.

Оптичні прилади призначені для створення зображення предмета. Кожний світний предмет або, що те саме, джерело світла, можна уявити собі як сукупність окремих світних точок. Зрозуміло, що зображення в цілому складається із зображень окремих точок. Тому спочатку розглянемо, як утворюється зображення окремої світної точки.

а) б) в)

Мал. 1

Із світної точки S, як із спільного центра промені розходяться в усіх напрямах (мал. 1, а). Такий пучок променів називають розбіжним гомоцентричним пучком (тобто розбіжним пучком, що має спільний центр). Якщо примусити хоча б частину променів розбіжного гомоцентричного пучка знову перетнутися в одній точці S′ (мал. 1, б), то вона й буде зображенням світної точки S.

Отже, щоб утворити зображення світної точки, треба перетворити розбіжний гомоцентричний пучок променів у збіжний,

Звідси випливає важливий висновок, який має значення для подальшого вивчення променевої оптики: незважаючи на те, що основним поняттям променевої оптики є поняття про промінь, у променевій оптиці цікавляться поведінкою не стільки одного променя, скільки сукупності променів Із спільним центром розбігу або збігу – гомоцентричними пучками променів світла. Отже, променева оптика є оптикою гомоцентричних пучків світла.

Логічно виникає питання, а яким чином, за допомогою чого можна розбіжні гомоцентричні пучки світла перетворювати в збіжні? Досвід підказує, що це можна зробити або за допомогою відбивання їх, або за допомогою заломлення на межі поділу двох середовищ. У такому разі необхідно вивчити закони відбивання і заломлення гомоцентричних пучків світла. Ці закони зручно вивчати на найпростішому гомоцентричному пучкові – пучку паралельних променів світла. Він має центр збігу у нескінченності (мал. 1, в). Досить простежити лише за одним променем світла у такому пучку, вивчити закономірності, яким він підлягає, оскільки всі промені пучка мають однакові властивості.

Вивчаючи закони відбивання, розглядають ідеальну дзеркальну плоску поверхню, яка повністю відбиває світло без поглинання. Певним наближенням до неї е плоске шліфоване та поліроване металеве дзеркало. (Бажано нагадати учням, що в цьому разі нерівності на плоскій поверхні будуть менші за розміри довжини хвилі).

У розробленій нами програмі спочатку подаємо учням основні поняття, потрібні для вивчення закону відбивання світла, а саме:

а) про кут падіння променя α, як кут між променем, що падає, і перпендикуляром, установленим до площини в точці падіння;

б) про кут відбивання γ. що визначається аналогічно (мал. 2);

в) про площину падіння, що проходить через падаючий промінь та перпендикуляр;

г) про площину відбивання, що визначається аналогічно до площини падіння.

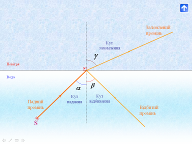
Мал. 2

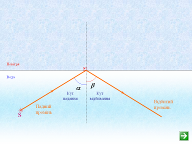
Нехай на ідеальну дзеркальну плоску поверхню падає під якимось кутом паралельний пучок світла (мал. 3, а). Простежимо за ходом одного з променів.

а) б)

Мал. 3

Закон відбивання складається з двох частин або правил:

1) падаючий промінь, перпендикуляр в точці падіння і відбитий промінь лежать в одній плішини (або площина падіння збігається, з площиною відбивання);

2) кут падіння променя світла дорівнює куту відбивання.

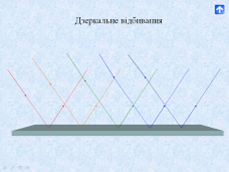
Отже, ідеальна плоска поверхня – дзеркало – не змінює вигляду або, як кажуть, структури паралельного пучка світла – він лишається і після відбивання паралельним і змінює лише напрям свого поширення. Таке підбивання називається дзеркальним.

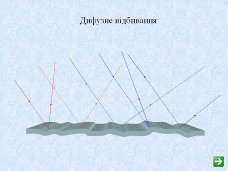
Металеві поверхні, лише шліфовані, але не поліровані, можуть мати окремі нерівності, розміри яких перевищують довжину хвилі. І тоді падаючий паралельний пучок після відбивання розсіюється (мал. 3, б), хоч переважна частина енергії світла все-таки поширюється в напрямі дзеркального відбивання. Коли нерівності нагромаджені хаотично (матові поверхні), паралельний пучок повністю розсіюється і напрям поширення енергії не залежить від напряму падіння (дифузне відбивання світла). Цей вид відбивання світла має дуже важливе значення в житті людей і тварин, бо дає змогу бачити не лише світні тіла, а й несвітні, що опромінюються джерелами світла.

Бажано підкреслити, що закон відбивання світла однаковий для променів усіх довжин хвиль.

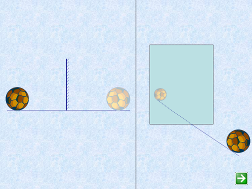
Установивши закон відбивання для паралельного пучка променів, перейдемо до розгляду відбивання від плоскої дзеркальної поверхні розбіжного гомоцентричного пучка променів світла. Основне питання, яке треба при цьому розв’язати: «чи можна за допомогою плоского дзеркала утворити зображення точкового джерела світла?» Користуючись законом відбивання світла, показуємо, що плоске дзеркало не має дійсного зображення точкового джерела (мал. 4). Розбіжний гомоцентричний пучок променів лишається розбіжним. Кут розхилу також не змінюється. Змінюється лише напрям поширення пучка. Отже, за допомогою плоского дзеркала не можна утворити дійсне зображення точкового джерела, а отже, і світного тіла в цілому. Проте учні з досвіду знають, що дзеркало утворює уявне зображення (мал. 4).

Мал. 4

Як можна ввести поняття про уявне зображення? Тут є два способи. Перший спосіб – зауважити, що уявне зображення утворюється лише при спостереженні оком і про нього мова буде пізніше, а другий – ввести це поняття уже на даному етапі. Це можна зробити так. Насамперед розповідають учням, не вдаючись до розгляду будови ока (вона вивчається пізніше), що спостерігач бачить зображення світної точки в тому місці, де перетинається обернене продовження світлових променів, які входять в око. Це зображення буде дійсним, якщо в тому місці розташоване реальне джерело світла або його реальне зображення, створене попередньою оптичною системою, або уявним, якщо в тому місці ні джерела, його дійсного зображення немає. Після такого попереднього зауваження можна розглянути уявне зображення точки або предмета, що його дає плоске дзеркало.

Щоб утворити дійсне зображення при відбиванні світла, очевидно, треба скористатися криволінійними поверхнями. Найважливіші з них – сферичні: такі поверхні порівняно легко шліфувати й полірувати, і вони дають потрібний ефект.

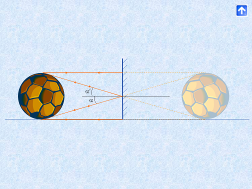
Якщо на сферичне дзеркало малої кривизни спрямувати паралельно головній оптичній осі не дуже великого перерізу паралельний пучок променів світла, то вони (з достатнім наближенням) перетнуться в одній точці на осі. Цю точку називають головним фокусом дзеркала. Ввівши поняття фокуса і променів побудови, можна перейти до побудови зображень у сферичних дзеркалах. На закінчення варто розповісти про використання сферичних дзеркал у науці й техніці.

Інша можливість, утворити зображення світної точки (або предмета) пов’язана з використанням закону заломлення світла. Щоб вивчити цей закон, розглянемо монохроматичний пучок паралельних променів світла, який падає на плоску межу поділу двох прозорих діелектриків.

На відміну від відбивання, промені різної довжини хвилі заломлюються по-різному, тому надалі, якщо не буде якихось додаткових умов, користуватимемося монохроматичним світлом.

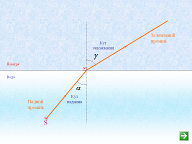
Простежимо за ходом заломлених променів (мал. 5).

Мал. 5

Закон заломлення світла, як і закон відбивання, також складається з двох частин:

1) падаючий і відбитий промені лежать в одній площині з перпендикуляром, проведеним у точці падіння;

2) відношення синуса кута падіння до синуса кута заломлення – величина стала для даних двох речовин, що межують, і є лише функцією довжини хвилі, а саме:.Стала n називається показником заломлення другою середовища відносно першого або просто відносним показником заломлення.

З хроматичності заломлення випливає обмеженість поняття променя. Ввівши поняття монохроматичного пучка променів, ми наближаємо променеву оптику до хвильової. Це доповнення дасть змогу і в хвильовій оптиці широко використовувати поняття променя.

З означення відносного показника заломлення випливає, що для кожної речовини він залежить від речовини, з якою вона межує. Щоб усунути цю неоднозначність, вводять поняття про абсолютний показник заломлення, коли межуючим середовищем є вакуум. Очевидно, для самого вакууму абсолютний показник заломлення дорівнює одиниці.

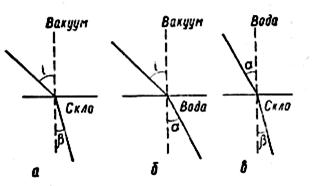
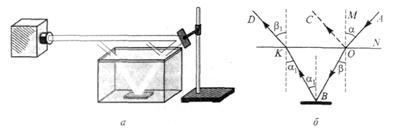
Пояснимо зв’язок між абсолютним і відносним показником заломлення світла. Розглянемо хід променів на межі води і скла. Якщо промінь з води потрапляє в скло під кутом α і заломлюється в склі під кутом β, то відносний показник заломлення скла відносно води буде . Припустимо тепер, що з вакууму промінь світла падає на скло під якимось кутом і (мал. 6, а), для якого кут заломлення дорівнює β. Тоді абсолютний показник заломлення для скла буде. Якщо з вакууму промінь світла падає на воду під тим самим кутом і (мал. 6, б), то кут заломлення α, як показує дослід, буде трохи більший за кут β для скла. А абсолютний показник заломлення для води  буде меншим за n_c. Це дає підставу ввести поняття оптичної густини речовини.

Мал. 6

Ту з двох речовин називають оптично густішою, абсолютний показник заломлення світла в якої більший. Це поняття полегшує вивчення явища повного відбивання світла та ряду інших явищ. Як правило, оптично густіші речовини мають також більшу густину речовини. Однак є й винятки. Наприклад, скипидар має абсолютний показник заломлення 1,47, а густину 0,87 г./см³, у той час як абсолютний показник заломлення льоду 1,31, а густина 0,92 г./см³.

Обчислюючи відношення абсолютних показників заломлення води і скла  дістаємо вираз, що дорівнює відносному показнику. Отже,  і звідси випливає, що відносний показник дорівнює відношенню абсолютних показників заломлення світла і є показником заломлення другої речовини (в яку поширюється заломлене світло) відносно першої (в якій падає світло).

Коли світло падає на межу поділу двох прозорих середовищ, то, крім заломлення, завжди відбувається також відбивання світла, закон якого ми вивчали раніше. Бажано, вивчаючи це питання, проаналізувати розподіл падаючої енергії між відбитою та заломленою. Нагадуємо учням, що частка відбитої (а отже, і заломленої) енергії світла залежить як від оптичних властивостей межуючих середовищ, так і від значення кута падіння. Якщо, наприклад, світло падає з повітря на скляну пластинку перпендикулярно до її поверхні (α=0), то відбивається всього близько 5% енергії, а 95% енергії проходить через межу поділу. При збільшенні кута падіння частка відбитої енергії зростає і при ковзному падінні (α=90°) світло відбивається майже повністю.

Доцільно звернути увагу учнів на те, що відбивання світла все ж ніколи не буває повним. Навіть для кутів падіння, близьких до 90°, частина енергії все-таки переходить у друге середовище. Проте у випадку падіння світла з оптично густішого в оптично менш густе середовище за певних умов можливе повне відбивання світла. І в цьому разі частка відбитої енергії зростає із збільшенням кута падіння, проте за іншим законом: починаючи з якогось кута падіння, що називається граничним, світло повністю відбивається від межі поділу. Це явище називають повним відбиванням (мал. 7). Часто його називають також явищем повного внутрішнього відбивання. Останнє твердження не суперечить попередньому, бо повне відбивання може бути тільки внутрішнім.

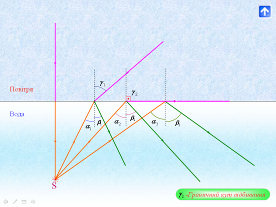
Мал. 7

Як і при заломленні на плоских поверхнях, тут доцільно розглянути практично важливий випадок – заломлення гомоцентричних пучків променів світла на прозорій речовині, обмеженій сферичними поверхнями. Такий пристрій називають лінзою (мал. 8). Пряма, що проходить через центри кривизни заломлюючих поверхонь О і О₁, називається оптичною віссю. Оптична вісь перетинає заломлюючі поверхні в точках А і В. Для дуже тонких лінз, які ми розглядатимемо, ці дві точки зливаються в одну, яку називають оптичним центром лінзи.

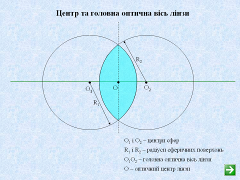
Мал. 8

Потім вводимо поняття про фокус і фокальну площину. Можна почати з демонстрації, спрямувавши на просту лінзу, прикриту непрозорим екраном з невеликим отвором у центрі, паралельний пучок світла. Промені, що проходять через відкриту Чистину лінзи, після заломлення проходять через деяку точку F осі. Якщо в цій точці поставити екран, то в місці перетину променів побачимо невеличку яскраву пляму. Прийнявши діафрагму, помітимо, що пляма розширюється. Звідси робимо важливий висновок, що проста лінза збирає паралельний пучок променів у точку лише за умови, коли переріз його невеликий. Визначаємо поняття фокуса як точки, в якій перетинається паралельний пучок променів, що падає паралельно оптичній осі, і фокальної площини, що проходить через фокус перпендикулярно до оптичної осі. У фокальній площині перетинаються вузькі паралельні пучки Променів, які падають під невеликим кутом до оптичної осі. Точка перетину лежить там, де зустрічає фокальну площину промінь, що проходить без заломлення через оптичний центр лінзи. Зазначаємо, що довільний промінь, паралельний до оптичної осі, після заломлення проходить через фокус, а промінь, що проходить через оптичний центр лінзи, не заломлюється.

Проробимо такий дослід. Помістимо лампу розжарювання з прозорим скляним балоном за фокальною площиною задіафрагмованої лінзи, неподалік від її оптичної осі. У певній площині за лінзою легко відшукати чітке і яскраве зображення розжареної нитки лампи. Утворення зображення можна пояснити так. Кожна світна точка S нитки має зображення S₁ у пивній площині поза лінзою. Оскільки світний предмет можна розглядати як сукупність окремих світних точок, то в тій самій площині дістанемо зображення нитки лампи. Площина предмета і площина зображення називаються спряженими площинами. Отже, лінза перетворює розбіжний пучок променів, що падає на неї від кожної точки предмета, в збіжний пучок у спряженій площині. Щоб знайти положення точки S₁, можна простежити за ходом через лінзу будь-яких двох променів гомоцентричного пучка, оскільки точка визначиться перетином двох прямих. У загальному випадку для цього треба було б виміряти кути падіння на першу й другу поверхні лінзи кожного з цих двох променів і, знаючи показник заломлення скла, визначити їх напрями після проходження через лінзу. Можна зробити інакше: знаючи положення фокуса, скористатись для знаходження зображення не довільними променями, а тими, хід яких нам наперед відомий, наприклад, променем, що йде паралельно оптичній осі, та променем, що проходить через оптичний центр. Перший промінь після заломлення пройде через фокус лінзи, а другий взагалі не змінює свого напряму. Перетин цих двох променів дає змогу побудувати зображення точки S₁, якщо відоме положення лінзи, оптичної осі та її фокусів. Тому ці промені називають променями побудови. Отже, завжди, коли треба побудувати зображення, користуватимемося променями побудови. Щоб підкреслити практичне значення променів побудови, надалі зображатимемо їх пунктиром.

Якщо, виконуючи другий дослід, розширити задіафрагмовану частину лінзи і тим самим збільшити переріз гомоцентричних пучків, зображення розмивається і забарвлюється. Робимо висновок, що звичайна товста лінза не дає чіткого зображення предмета, бо вона не може збирати в одну точку широкі гомоцентричні пучки світла. Виникнення таких спотворень (аберацій) стане зрозумілим, якщо пригадати проходження широкого пучка променів через плоскопаралельну пластину, а також проходження пучка променів білого кольору через призму.

Отже, для лінз із значним отвором характерні аберації. В оптичних приладах отвори, як правило, великі, бо від них залежить кількість світлової енергії, що доходить до зображення. Користуючись лінзою, ми, з одного боку, зацікавлені в збільшенні її розміру, а з другого – вимушені його зменшувати. Виникає суперечлива ситуація. Який вихід з цього становища, розповімо нижче, а зараз, щоб вивчити побудову зображень залежно від того, як розміщено предмет відносно лінзи, доцільно ввести поняття про ідеальну лінзу. Під ідеальною лінзою розуміють нескінченно тонку лінзу, не обмежену за розмірами, яка паралельний пучок світла збирає в точку, незалежно від розмірів його перерізу і нахилу до оптичної осі. Така лінза перетворює розбіжний гомоцентричний пучок довільного перерізу, що виходить з точки поза фокусом, в ідеально збіжний.

Користуючись ідеальною збиральною лінзою, розглядаємо п’ять випадків положення предмета відносно лінзи та її фокусів (мал. 8):

1) за подвійною фокусною відстанню;

2) на подвійній фокусній відстані;

3) між фокусом і подвійним фокусом;

4) на фокусній відстані;

5) між фокусом і лінзою.

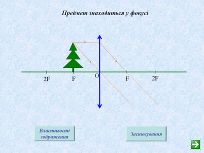
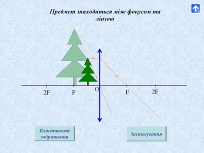
Мал. 8

В останньому випадку лінза дійсного зображення не дає: розбіжні гомоцентричні пучки, заломившись на лінзі, лишаються розбіжними. І лише в сукупності з оком можна дістати уявне зображення.

Тепер можна розповісти учням, що положення і розмір зображення відносно лінзи можна розрахувати також аналітично за допомогою формули лінзи. Є два варіанти пояснення цього питання. Перший раціонально застосувати тоді, коли учні добре підготовлені, а також коли є достатньо часу для розгляду питань променевої оптики або на факультативних заняттях. Подати цей матеріал можна в такому порядку, як він розглядається в посібнику з фізики. В цьому разі розкривається суть наближення при введенні тонкої лінзи, а також зазначається, як залежить фокусна відстань під показника речовини лінзи та від радіусів кривизни поверхонь, що її обмежують.

Другий підхід дещо формальний, але він веде безпосередньо до мети – встановлення формули лінзи. При ньому відразу розглядають тонку ідеальну лінзу і з суто геометричних міркувань виводять формулу лінзи, як це зроблено в підручнику.

Потім бажано знову повернутися до реальних лінз і пригадати, які їм властиві аберації. Доцільно навіть навести помилкове твердження Ньютона про те, що хроматичну аберацію подолати не можна і тому ніколи не вдасться утворити з лінзами якісного зображення. З цих міркувань Ньютон запропонував використовувати для астрономічних приладів відбивні дзеркала, які не мають хроматичної аберації.

Пізніше вчені спростували твердження Ньютона. Вони навчилися значною мірою долати всі аберації. Спеціальною комбінацією збиральної та розсіювальної лінз можна усунути хроматичну аберацію принаймні для двох довжин хвиль (мал. 8), а також сферичну аберацію. Ми розглянули лише принципову можливість усунення аберації, оскільки справа ця дуже складна. Потрібний великий асортимент оптичного скла з різноманітними показниками заломлення, крім того, треба провести попередні складні розрахунки.

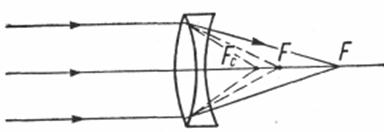
Мал. 8

Часто для усунення хроматичної аберації на значному спектральному інтервалі або занадто великої сферичної аберації, що виникає при заломленні ширококутних пучків променів, потрібні не дві, а кілька (3–10) лінз. Сукупність кількох лінз, з яких одна або дві основні, а решта – корегуючі, скріплених жорстокою оправою, називається об’єктивом.