Два цветка

3. Два цветка

Вы и компьютер одновременно показываете один или два цветка. Потом считают сумму показанных цветков, она может быть получена от двух до четырех (1 и 1, 1 и 2, 2 и 2). Если сумма является четной (2 или 4), компьютер выигрывает у вас; если же сумма является нечетной, то вы выигрываете у компьютера (рис. 20).

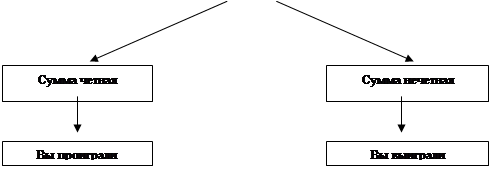
Рис. 20. Дерево игры “Два цветка”

4. Пальцы

Вы и компьютер играете на очки. Вы оба одновременно показываете сколько-то пальцев.

Если количество пальцев оказалось одинаковым, то ничья.

Если число пальцев, показанных вами и компьютером, отличается на единицу, то тот, кто показал меньше пальцев, получает два очка.

В остальных случаях, тот, кто показал больше пальцев, получает одно очко (рис.21).

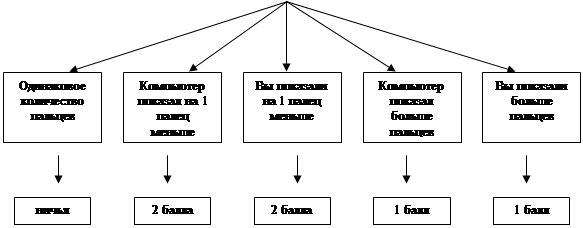
Рис.21. Дерево игры “Пальцы"

Про лыжников.

Два спортсмена бегут по лыжной трассе друг другу на встречу. Перед каждым из них стоит выбор либо уступить, либо не уступить. Тот, кто уступит дорогу потеряет на этом 2 секунды, иначе если никто не уступит и они столкнутся, то будут распутываться 10 секунд (рис.22).

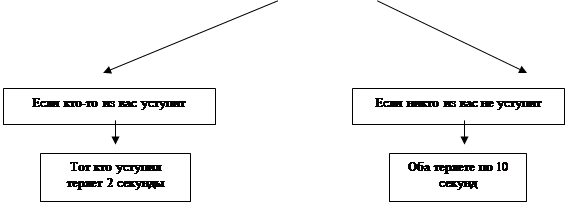
Рис.22. Дерево игры “Про лыжников"

Торговцы на станции

На станции Шершни трое местных продавцов, Андрей, Василий и Семен, продают пассажирам, соответственно, ткань, нитки и иголки. Утром приходят сразу два поезда, поэтому каждый спешит выставить свой товар на первой или второй платформе. Если продавец работает на платформе в одиночку, его выручка от продажи товаров пассажирам соответствующего поезда определяется из таблицы:

Таблица 5

Платформа	Андрей	Василий	Семен
1	80	60	60
2	100	40	40

Если в одном месте продаются и ткань и нитки, то этих товаров удастся продать на 50 процентов больше, из-за того что эти товары дополняют друг друга. Впрочем если продавец ниток и продавец иголок находятся на одной платформе, то вследствие конкуренции оба выручают вдвое меньше, чем когда они находятся на разных платформах (рис.23).

Первая платформа Вторая платформа

 

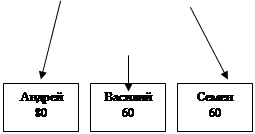
Рис.23. Дерево игры “Торговцы на станции”

Продавцы мороженого на пляже.

На городском пляже стоят два ларька с мороженым. Продавцы независимо друг от друга устанавливают цены. Выглядит это примерно так:

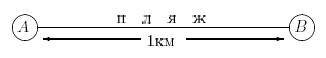
Отдыхающие равномерно распределены по пляжу и загорают. В этот день очень жарко, поэтому каждый готов переплатить за мороженое рубль, только бы не идти лишние 100 метров по горячему песку (рис.24).

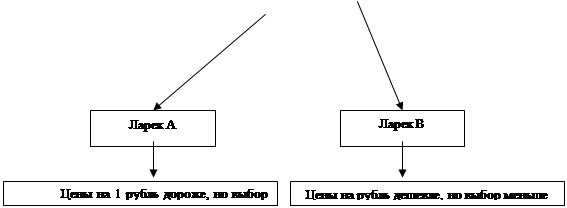
Рис.24. Дерево игры “Продавцы мороженого на пляже"

Аукцион печенья.

Имеется пакет с печеньем, который нужно поделить между несколькими участниками. Сколько печенья в пакете никому не известно. Каждый участник тайно от других пишет на листке бумаги свое имя и сколько печенья он бы хотел получить. Все заявки упорядочиваются по возрастанию, после чего ведущий по очереди выдает каждому запрошенное им количество, начиная с тех кто написал самое меленькое количество печенья. Если в некоторый момент печенье заканчивается, то те кто заявили слишком много, увы, остаются ни с чем. (Если оставшегося печенья оказывается не достаточно, чтобы обслужить несколько одинаковых заказов, то делим между ними поровну) Если же остались лишние печенья, то они достаются ведущему (рис.25).

Рис.25. Дерево игры “Аукцион печенья”

Баше

В игре вы ходите по очереди. На столе лежит куча камней, количество камней никому не известно. В свой ход можно взять от одного до четырех камней. Выигрывает тот, кто своим ходом оставляет пустой стол (рис.26).

		Вы выиграли				Вы проиграли

Рис.26. Дерево игры “Баше"

Приложение 2

Контрольная работа

Тестовые задания (максимальное количество баллов = 8).

Теоретические:

1) Выберете правильный вариант. Что называется последовательностью действий ограниченных определенными правилами?

Задача

Игра

Ситуация

2) Выберете правильный вариант. Кем могут определятся правила игры?

Участниками игры

Одним из участников игры

Компьютер

3) Выберете правильный вариант. Что можно назвать положительным исходом игры?

Проигрыш

Приз

Выигрыш

4) Выберете правильный вариант. Что мы подразумеваем под правилами игры?

Система неизвестных

Система решений

Система условий

5) Выберете правильный вариант. Кого можно назвать основоположником Теории игр?

Джон фон Нейман

Исаак Ньютон

Архимед

6) Выберете правильный вариант. Игры можно классифицировать как:

Одно-выигрышные и много выигрышные

Одноходовые и многоходовые

Одношаговые и многошаговые

7) Выберете правильный вариант. Что может служить примером случайного хода?

Бросание монеты

Шахматы

Игра в карты

8) Выберете правильный вариант. Участники игрового процесса это -

Люди

Игроки

Ученики

Практические задания (максимальное количество баллов =12)

I вариант

1) Из исходного рисунка попробуйте сформулировать условие задачи, которая начинается так - У вас с товарищем имеется по 2 цветка. Вы и ваш товарищ одновременно показываете один или два цветка. Потом считают сумму показанных цветков, она может быть получена от двух до четырех (см. рис.27).

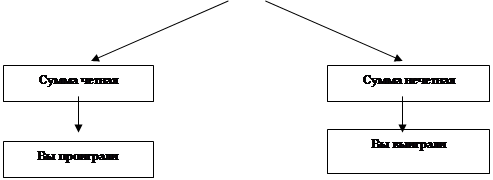
Рис.27. Дерево игры.

2) Определите выигрышную стратегию следующей игры: В игре вы ходите по очереди. На столе лежит куча камней, количество камней никому не известно. В свой ход можно взять от одного до четырех камней. Выигрывает тот, кто своим ходом оставляет пустой стол.

II вариант

1) Попробуйте сформулировать правила игры в Крестики-Нолики.

2) Попробуйте нарисовать дерево решения следующей задачи:

Вы и ваш товарищ играете на очки. Вы оба одновременно показываете сколько-то пальцев. Если количество пальцев оказалось одинаковым, то ничья. Если число пальцев, показанных вами и товарищем, отличается на единицу, то тот, кто показал меньше пальцев, получает два очка. В остальных случаях, тот, кто показал больше пальцев, получает одно очко.

Таким образом, максимальное количество баллов, которые может набрать учащийся = 20 (8 +12). Что соответствует уровням компетенций учащихся следующим образом: 7 - 10 - 1 уровень; 11 - 15 - 2 уровень; 16 - 20 - 3 уровень;

Приложение 3

Урок 1.

Тема урока: Что такое игра.

Тип рока: объяснение нового материала.

Цели урока:

Развивающая: развивать у учащихся познавательные интересы, мышление; развивать культуру высказывания собственного мнения.

Воспитательная: приучать учащихся к внимательности при объяснении нового материала.

Практическая: иметь представление об играх, уметь отвечать на вопросы учителя, уметь приводить свои примеры.

Методические и технические средства: проектор, доска, маркер, тетради

Основные понятия: игра, выигрыш, виды игр.

Методические рекомендации учителя по проведению урока: Так как это первый урок, то вы должны объяснить учащимся чем они будут заниматься на следующих уроках этого курса. Что же касается непосредственно этого урока, то он должен пройти в виде беседы на тему различных игр, то есть вы им рассказываете о играх, приводите какие-то свои примеры, просите их о чем-нибудь рассказать. Спросите, в какие игры они играют и что им нравятся. Также вам необходимо затронуть некоторые определения и записать их в тетради. Все что им необходимо законспектировать желательно оформить в виде презентации. Ближе к концу урока можно предложить поиграть в какую-либо игру для всего класса.

Контрольные вопросы:

1. Что такое игра?

2. Примеры игр.

3. Что такое выигрыш?

4. Назвать основные виды игр.

5. Кого можно назвать основателем Теории игр?

6. Что изучает Теория игр?

Этапы урока:

1) Организационный момент (2 мин).

2) Объяснение нового материала (35 мин)

3) Подведение итогов и выдача домашнего задания (3 мин).

Таблица.

Этап	Учитель	Ученик	Доска	Тетрадь	Время
Организационный момент.	Здравствуйте дети. Садитесь. Меня зовут Новикова Ксения Сергеевна. Я буду вести у вас некоторое время уроки информатики.	Приветствуют учителя.			2 мин
Объяснение нового материала.	В курсе наших занятий мы с вами должны познакомится с некоторыми элементами теории игр. Значит ТИ это такой раздел математики, который изучает разного вида игры. Сегодня на уроке мы с вами познакомимся с что же такое игра. Вы все наверняка играете в игры. А кто-нибудь из вас когда-нибудь задумывался о том, кто и при каких обстоятельствах их придумал? И вообще откуда появились игры. Для людей игры есть и были как развлечения, иногда даже и как соревнование. Например, игры в шашки, шахматы и карты. Ну, теперь давайте вернемся непосредственно к нашей теме. Теория игр, о которой мы с вами будем говорить, была основана Джоном фон Нейманом. Давайте попробуем сформулировать определение игры. Что нам об этом известно? То есть, при каких условиях осуществляется игра? Вы же не можете просто придумать любое название игры и сразу же в нее играть, ведь этого будет не достаточно. Не так ли? Да, правильно она идет по правилам. И так мы с вами получили, что игра - это последовательность действий ограниченных определенными правилами. Теперь откройте свои тетрадки, запишите число и тему урока “Что такое игра”. После этого - определение игры, которое на доске. Правила игры может устанавливать любой человек, который вам объясняет, как в нее играть. Также в процессе игры, сами участники могут договорится об изменение какого-либо условия. Можете привести примеры каких-нибудь игр и рассказать по каким правилам они ведутся? Хорошо. Например, всем хорошо знакомая игра в прятки. Представьте, что я не знаю как в нее играть и кто мне может объяснить как это делается? Отлично. Вот вы играете в крестики - нолики и обязательно кто из вас должен выиграть, а кто-то проиграть. Верно? И ваш выигрыш будет называться положительным исходом игры. Давайте это с вами запишем, выигрыш - положительный исход игры. Дальше мы с вами рассмотрим, какие существуют виды игр. Например, они могут быть парными, то есть игроки в процессе игры объединяются в пары. Хотя можно и играть по одному. Наверняка, многие из вас видели, как играют в бадминтон, обычно они играют один на один, а еще можно играть в парах, то есть два против два. Кто может привести пример подобной ситуации? Молодцы. Следующая классификация характеризуется количеством ходов. Игры делятся на: одноходовые - здесь выигрыш распределяется после одного хода каждого игрока и многоходовые соответственно выигрыш распределяется после нескольких ходов. Примерами одноходовых игр могут служить спор на кулачках. После одного скидывания вам уже известно кто проиграл спор. Попробуйте привести свои примеры. Хорошо. Ну, а примерами многоходовых игр можно назвать игры в шашки, шахматы, карты. Какие примеры вы можете привести здесь? Хорошо. Все справились с заданием. Ну а теперь у нас отсталость еще время и я предлагаю вас сыграть в одну очень простую игру. Кто хочет принять участие, мне нужно двое желающих. Правила игры следующие: Двое играют в игру: первый называет однозначное число (то есть целое число от 1 до 9 включительно), второй прибавляет к нему еще какое-нибудь однозначное число и называет сумму, к этой сумме первый прибавляет еще какое-нибудь однозначное число и опять называет сумму и так далее. Выигрывает тот, кто первым назовет число 66.	Отвечают на поставленный вопрос.   Отвечают, что она выполняется по правилам. Приводят свои примеры. Объясняют игру в прятки.   Приводят свои примеры. Приводят свои примеры. Приводят свои примеры.	Что такое игра.     игра - это последовательность действий ограниченных определенными правилами.   Выигрыш - положительный исход игры	Что такое игра.     игра - это последовательность действий ограниченных определенными правилами.   Выигрыш - положительный исход игры	35 мин
Подведение итогов и выдача домашнего задания.	Сегодня на уроке мы с вами познакомились с некоторой информацией об играх, о которой вы даже никогда и не думали, о том как их классифицируют. Теперь откройте свои дневники и запишем домашнее задание. Дома вам нужно будет выучить определение игры и выигрыша. Всем спасибо. До свидания.	Записывают домашнее задание.			3 мин

Урок 2.

Тема урока: Основные понятия Теории игр.

Тип рока: комбинированный урок: объяснение нового теоретического материала и рассмотрение практических примеров.

Цели урока:

Развивающая: развивать у учащихся познавательные интересы, познавательные и творческие способности.

Воспитательная: приучать учащихся к внимательности при объяснении нового материала.

Практическая: приводить примеры на изученную тему

Методические и технические средства: проектор, доска, маркер, тетради, раздаточный материал.

Основные понятия: игра, игроки, правила, ход, стратегии.

Методические рекомендации учителя по проведению урока: Продолжаете знакомить учеников с основными понятиями. Все определения, которые встретятся на этом уроке можете оформить в виде презентации. На практическом примере попытайтесь, чтобы учащиеся сами выявили основные понятия, с которыми они уже ознакомлены, то есть предлагаете им какую-нибудь игру и по ней они должны определить где правила, сколько игроков и возможную стратегию.

Контрольные вопросы:

1. Что такое правила игры? Как вы это понимаете?

2. Попробуйте определить правила для крестиков и ноликов.

3. Дайте определение партии.

4. Как вы понимаете ход в игре?

5. Объясните на примере что такое стратегия.

Этапы урока:

1) Организационный момент (2 мин).

2) Объяснение нового материала (30 мин)

3) Применение нового материала на практике (10 мин).

4) Подведение итогов и выдача домашнего задания (3 мин).

Таблица.

Этап	Учитель	Ученик	Доска	Тетрадь	Время
Организационный момент	Здравствуйте. Садитесь. Давайте отметим отсутствующих.				2 мин
Объяснение нового материала.	На прошлом занятии мы с вами познакомились с игрой, с условиями определяющими ее, с понятием выигрыша и рассмотрели классификацию игр. Наш урок мне бы хотелось начать с опроса. Вашим домашним заданием было - выучить что такое игра и выигрыш. Кто мне скажет что такое игра? Если не можете дать точное определение, попробуйте объяснить своими словами. Выигрыш? Сегодня мы с вами познакомимся еще с некоторыми понятиями Теории игр, такими как: ход, игроки, правила игры, стратегия. Мы с вами очень много говорили о правилах игры, теперь давайте дадим определение. Под правилами игры мы понимаем систему условий, которая определяет возможные варианты действий игроков. Откройте свои тетради, запишите число и тему урока “Основные понятия Теории игр”, а также что такое правила игры. Под игроками мы подразумеваем самих участников игрового процесса. Не дамою, что это нужно записывать, ведь вы и так запомните. Партия, наверняка многие слышали это понятие, - можно назвать вариант осуществления игры каким-либо образом. Соответственно партия состоит из ходов. Ходом можно назвать допустимый вариант поведения в игре. Они бывают личные и случайные. Примером личного хода может быть игра в шахматы, а случайного бросание монеты. Еще нам осталось познакомится с таким понятием как стратегия. Точное определение стратегии следующее - совокупность правил, однозначно определяющих последовательность действий игрока в каждой конкретной ситуации, складывающейся в процессе игры. Другими словами - это выбранная вами, определенная последовательность ходов. Подробнее можно разобрать на примере. Вы и ваш товарищ скидываетесь на кулачках, вы постоянно показываете “ножницы", думая, что возможность того, что вы выиграете больше - это и есть в данном случае ваша стратегия. Ну, а та стратегия, которая обеспечит вам наибольший выигрыш называется выигрышной стратегией. Попробуйте привести свои примеры. Теперь давайте немного запишем все, о чем мы говорили. Игроки - участники игрового процесса. Партия - вариант реализации игры каким-либо образом. Ход - допустимый вариант поведения в игре. Стратегия - совокупность правил, однозначно определяющих последовательность действий игрока в каждой конкретной ситуации, складывающейся в процессе игры.	Слушают. Отвечают. Записывают. Приводят примеры.	“Основные понятия Теории игр" Правила игры - система условий, которая определяет возможные варианты действий игроков. Игроки - участники игрового процесса. Партия - вариант реализации игры каким-либо образом. Ход - допустимый вариант поведения в игре. Стратегия - совокупность правил, однозначно определяющих последовательность действий игрока в каждой конкретной ситуации, складывающейся в процессе игры.	“Основные понятия Теории игр" Правила игры - система условий, которая определяет возможные варианты действий игроков. Игроки - участники игрового процесса. Партия - вариант реализации игры каким-либо образом. Ход - допустимый вариант поведения в игре. Стратегия - совокупность правил, однозначно определяющих последовательность действий игрока в каждой конкретной ситуации, складывающейся в процессе игры.
Применение нового материала на практике.	До конца урока у нас еще осталось время и мне бы хотелось продемонстрировать вам пример одной игровой ситуации. Сейчас все внимание на доску. Условия этой игры таковы: Вы и ваш товарищ одновременно показываете один или два цветка. Потом считаете сумму показанных цветков, она может быть получена от двух до четырех (1 и 1, 1 и 2, 2 и 2). Если сумма является четной (2 или 4), ваш товарищ выигрывает у вас; если же сумма является нечетной, то вы выигрываете у него. Например, я выбираю один цветок, а мой соперник показал 2так как сумма нечетная - я выиграла. Скажите мне, что является правилами этой игры? Ходом? Игроками? Сейчас я вам раздам цветочки из бумаги и вы попробуете поиграть с товарищами по парте.	Отвечают на вопросы.
Подведение итогов и выдача домашнего задания.	Сегодня мы познакомились еще с некоторыми понятиями, которые вам дума предстоит выучить. Запишите себе в дневник выучить определения правила игры, ход, партия, стратегия. Увидимся на следующей неделе. До свидания.	Записывают домашнее задание.