Навигация
Мотивация изучения теорем
3.2 Мотивация изучения теорем.
При введении теоремы можно условно выделить следующие этапы ее изучения:
- мотивация изучения теоремы и раскрытие ее содержания (усмотрение геометрического факта и формулировка теоремы);
- работа нал структурой теоремы;
- мотивация необходимости доказательства теоремы;
- построение чертежа и краткая запись содержания теоремы;
- поиск доказательства, доказательство и его запись;
- закрепление теоремы;
- применение теоремы.
Для мотивации изучения теорем можно предложить такие приемы:
Прием 1. Обобщение наблюдаемых в жизни фактов и явлений и перевод их на математический язык.
Мотивировать необходимость изучения свойства «Две различные прямые либо не пересекаются, либо пересекаются только в одной точке» можно, предложив предварительно учащимся решить дома следующие задачи:
На плане местности четыре населенных пункта отмечены точками А, В, С, К. Выясните, пересекутся ли пути из пункта А в пункт С и из пункта К в пункт В (пути считаем прямолинейными). Если пересекутся, то в скольких точках? Рассмотрите различные возможные случаи расположения населенных пунктов. Могут ли эти пути пересекаться в двух точках?
В классе учитель выясняет полученные результаты решения задачи: во всех случаях пути движения либо имеют одну общую точку, либо не имеют ни одной. Отметив, что пути движения в данных задачах были отрезками, предлагается подумать над вопросом: измениться ли вывод, если вместо двух отрезков взять две прямые?
Ответы могут быть разными. Если ответы разные, то сразу можно предложить выяснить, могут ли две прямые иметь две общие точки, и тем самым перейти к доказательству теоремы, мотив изучения которой стал очевиден. Если же ответ один, то есть две различные прямые пересекаются в одной точке, то учитель говорит, что в этой задаче это действительно так. При решении других задач может быть по-другому: ведь вы не можете рассмотреть все конкретные жизненные ситуации и прорешать все задачи.[13]
С теоремой о сумме углов треугольника учащиеся могут ознакомиться, измеряя непосредственно углы треугольника. Обобщая результаты измерений, учащиеся приходят к выводу, что сумма углов треугольника равна 180°.[19]
Прием 2. Показ необходимости знания той или иной теоремы для решения практических задач.
Для мотивации изучения теоремы «Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны» можно использовать следующую задачу:

![]()
![]()
 А В
А В
С
![]() М
М
Д рис.1
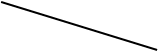
Картографам необходимо было нанести на карту два населенных пункта А и В (рис.1). Измерить расстояние между пунктами оказалось невозможно, так как между ними было озеро. Картографы поступили следующим образом: они выбрали точку С, от которой можно измерит расстояние и до пункта А и до пункта В. Измерили эти расстояния и построили на бумаге расстояния АС и СВ соответствующей длины (масштаб можно указать по своему усмотрению), а затем продолжили линии за точку С, отложили отрезки СД и СМ, равные соответственно отрезкам СВ и СА, и соединили точки Д и М отрезком. Картографы считают, что расстояние ДМ равно расстоянию АВ (в соответствующем масштабе). Правы ли картографы?
- По условию задачи известно, что АС = СМ, ВС = СД и, кроме того, АСВ = ДСМ как вертикальные углы.
- Надо установить, что ДМ = АВ.
- Откуда может следовать равенство этих отрезков?
- Равенство отрезков ДМ и АВ может следовать из равенства треугольников АСВ и ДСМ.
- Но в равных треугольниках соответственно равны все шесть элементов (по три угла и по три стороны), а здесь мы имеем только две стороны и угол между ними одного треугольника, соответственно равные двум сторонам и углу между ними другого треугольника.
- Следует доказать, что если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника равны.[13]
Мотив изучения и необходимость доказательства теоремы показаны.
Прием 3. Показ необходимости знания той или иной теоремы для решения задач и доказательства других теорем.
Например, перед доказательством теоремы «В равнобедренном треугольнике углы при основании равны» учащимся предлагается решить задачу:
В равнобедренном треугольнике АВС (АВ=ВС) вершина угла В соединена с серединой К стороны АС отрезком. Докажите, что треугольники АВК и СВК равны. Достаточно ли этих данных, чтобы установить равенство названных треугольников.
Так как третьего признака равенства по трем сторона у учащихся пока нет, то данную задачу они решить не могут. Созданная проблемная ситуация позволяет сразу мотивировать необходимость изучения сразу трех теорем : «В равнобедренном треугольнике углы при основании равны», «В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой», «Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны».[13]
Прием 4. Показ, как решалась данная проблема в истории науки.
Например, перед изучением второго признака равенства треугольников, можно привести историческую справку.
|
|
|
|
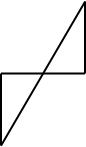 Пусть А – точка берега (рис.2), В – корабль на море. Для определения расстояния АВ восстанавливают на берегу перпендикуляр произвольной длины: АС⊥АВ; в противоположном направлении восстанавливают СЕ⊥АС так, чтобы точка Д (середина АС), В и Е находились на одной прямой. Тогда СЕ будет равна искомому расстоянию АВ.[4]
Пусть А – точка берега (рис.2), В – корабль на море. Для определения расстояния АВ восстанавливают на берегу перпендикуляр произвольной длины: АС⊥АВ; в противоположном направлении восстанавливают СЕ⊥АС так, чтобы точка Д (середина АС), В и Е находились на одной прямой. Тогда СЕ будет равна искомому расстоянию АВ.[4] После этой справки учитель задает вопрос, а прав ли Фалес, утверждая, что СЕ=АВ. Ответы учеников могут разделиться. Далее учитель вводит теорему: «Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны». Пользуясь данной теоремой, ученики без труда ответят, что треугольники АВД и СЕД равны, а значит и соответственные стороны АВ и СЕ равны.
Проследим мотивационный этап работы над теоремой на примере теоремы: «В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой».
Один из приемов мотивации изучения данной теоремы – знание теоремы для решения задач.
|
|
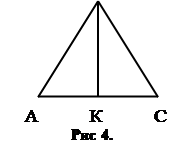 | |||
 | |||
С целью мотивации изучения этой теоремы можно использовать решение практической задачи.
|
 |  | ||||
| |||||
Можно использовать решение учебно-практической задачи:
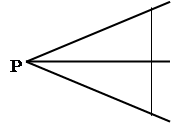
Чтобы разделить угол Р пополам с помощью только масштабной линейки, поступают так: 1) откладывают на сторонах угла Р (рис.6) равные отрезки РМ и РК; 2) соединяют точки М и К отрезком; 3) делят отрезок МК пополам, получают точку В; 4) проводят луч РВ. РВ – искомая биссектриса, разделившая угол пополам. Почему?[13]
Похожие работы
... среды, какие именно из психических функций задержались в развитии, когда и насколько, и другие психологические особенности ребенка. 2. Формирование мотивации учебной деятельности с задержкой психического развития Систематическая целенаправленная коррекционно-развивающая работа в условиях специальной школы способствует формированию учебной мотивации подростков с задержкой психического ...
... , которая призвана возбудить интерес к учению, сделать учение увлекательным, мобилизировать психологическую энергию и усилия, поддержать стремления, преумножить любознательность и старания. Мотивы и стимулы в учебной деятельности школьников долгое время находились как бы на периферии педагогических исследований. Большую помощь в разработке этой проблемы оказали психологи. Однако, с конца 70-х гг. ...
... : получить желаемые подарки от родителей, похвалу родителей и учителей, желание стать отличником, выделиться среди товарищей и т.п. Формирование мотивации учения школьника должно происходить на основе четко поставленной цели — получения хорошего образования. Очевидно, что не каждый ребенок с раннего возраста понимает, что он учится, прежде всего, для себя, для своих дальнейших достижений. Поэтому ...
... т. е. формы представления информации, методы первичного анализа данных, логика применения математических методов. 1. В качестве цели нашего исследования мы определили особенности мотивации учебной деятельности студентов гуманитарных факультетов университета. Концептуальная схема исследования представлена в Приложении Б. Далее в Программе исследования нами определены предмет, объект, цели, задач, ...

0 комментариев