Методика вивчення табличного і позатабличного множення та ділення

2 Методика вивчення табличного і позатабличного множення та ділення

 

2.1 Засвоєння таблиць множення та ділення

Однією з основних тем програми з математики для II класу є множення і ділення в межах 100. Ця тема включає ряд питань теорії, на основі якої вивчають табличне множення і ділення, позатабличне множення і ділення, ділення з остачею і особливі випадки множення та ділення (з одиницею і нулем).

До табличного множення належать випадки множення одноцифрових натуральних чисел на одноцифрові натуральні числа, результати яких визначають на основі змісту дії множення (знаходять суми однакових доданків), наприклад: 8 • 2, 6 • 3, 5 • 4.

Випадки ділення, які відповідають цим прикладам, також називають табличними, наприклад: 16: 2, 18: 6.

До позатабличних випадків належать множення і ділення в межах 100 двоцифрового числа на одноцифрове, множення одноцифрового на двоцифрове, а також ділення двоцифрового числа на двоцифрове.

До особливих випадків належать множення і ділення з числом нуль, а також множення і ділення на 1.

Внаслідок вивчення множення і ділення в межах 100 учні повинні засвоїти певний обсяг теоретичних знань: поняття про дії множення і ділення, зв’язок між компонентами і результатами дій множення і ділення, деякі властивості дій; знати напам’ять таблицю множення і відповідні випадки ділення, засвоїти ряд обчислювальних прийомів.

Розглянемо методику роботи над кожним з названих розділів.

Табличне множення і ділення. Табличне множення і ділення вивчають у два етапи. На першому етапі формують знання про самі дії множення і ділення, на другому – основну увагу приділяють засвоєнню учнями таблиць множення і відповідних випадків ділення.

На першому етапі насамперед розкривають конкретний зміст множення і ділення.

Множення і ділення з початку їх вивчення доцільно розглядати окремо, оскільки основним при цьому є розкриття не взаємозв’язку між ними, а конкретного змісту цих дій.

Множення розглядають як знаходження суми однакових доданків. Діти повинні засвоїти зв’язок між додаванням і множенням, навчитися розуміти зміст кожного компонента добутку: число, яке беруть доданком, – перший множник; число, яке показує, скільки однакових доданків, – другий множник. Конкретний зміст ділення розкривають за допомогою відповідних операцій з множинами, під час розв’язування задач на ділення на вміщення і на рівні частини.

Розкриваючи конкретний зміст множення, треба насамперед розширити досвід учнів у виконанні відповідних операцій над множинами. Ще в І класі під час вивчення нумерації, додавання і віднімання в межах 10 і 100 доцільно ввести лічбу пар предметів, трійок і т. д. і пропонувати задачі (приклади) на знаходження суми однакових і неоднакових доданків:

1) У трьох коробках лежить по 6 олівців. Скільки всього олівців у коробках?

2) У першій коробці 3 олівці, у другій – 6, у третій – 8. Скільки всього олівців у коробках?

Такі задачі (приклади) корисно ілюструвати предметами або малюнками. Треба практикувати і обернені вправи: за даними малюнками скласти задачі (приклади) на додавання. Розв’язуючи такі задачі і приклади, учні помічають, що є суми з однаковими доданками, і лічать, скільки таких доданків.

У II класі суму однакових доданків замінюють добутком:

6 + 6 + 6 + 6 = 24; 6 • 4 = 24.

Виконуючи цю операцію, діти ознайомлюються з дією множення, знаком і записом множення, засвоюють роль множників.

Покажемо, як це можна зробити.

Учитель пропонує розв’язати задачу: «Дівчинка наклеїла марки на 4 сторінки альбому, по 5 марок на кожну. Скільки всього марок наклеїла дівчинка?» Зробивши ілюстрації, учні записують розв’язок: 5 + 5 + 5 + 5 = 20.

Що можна сказати про доданки цієї суми? (Однакові.) Скільки їх? (4.) Тут по 5 взяли 4 рази. Якщо доданки однакові, то суму можна записати інакше:

5 • 4 = 20.

Читають цей запис так: по 5 узяти 4 рази, буде 20. (Діти повторюють.) Можна прочитати інакше: 5 помножити на 4, буде 20. (Повторюють.) Тут виконали дію множення. Додавання однакових доданків називають множенням. (Повторюють.) Множення позначають знаком – крапкою. Що показує в цьому записі число 5? (Число 5 береться як доданок.) Що показує число 4? (Скільки разів узяли доданком число 5.)

Потім розв’язують кілька вправ на заміну суми добутком. При цьому діти встановлюють, що показує кожне число в новому записі. Потім пропонують обернені вправи: на заміну добутку сумою. Наприклад, пропонують знайти результат: 3 • 4.

Прочитайте приклад. (З помножити на 4.) Що в ньому записі показує число 3? (Це число береться як доданок.) Що означає число 4? (Стільки береться доданків.) Замінимо приклад на множення прикладом на додавання. Запис: 3 + 3 + 3 + 3 = 12.

Щоб засвоїти зв’язок множення з додаванням, корисно розглянути такі вправи: читання прикладів на множення, записування аналогічних прикладів під диктовку спочатку вчителя, а потім учня, складання учнями прикладів на додавання і множення, розв’язування простих задач на знаходження добутку додаванням і множенням.

Дуже важливо, щоб учні зрозуміли, за яких умов можна замінювати суму добутком і коли це неможливо. Цьому допомагає розв’язування прикладів з однаковими і різними доданками.

На дошці приклад: 7 + 7 + 7.

Замініть приклад на додавання прикладом на множення (7 • 3.) Чи можна приклад 2 + 3 + 7 замінити прикладом на множення? (Не можна.) Чому? (Доданки різні. Доданки неоднакові.) Чи завжди можна приклад на додавання замінити прикладом на множення? (Не завжди.) Коли це можна зробити? (Коли доданки однакові.)

Можна запропонувати: скласти з однаковими числами приклади на додавання і множення, користуючись рисунками (рис. 1).

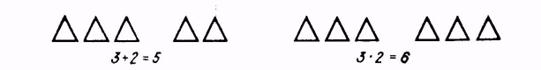
Рис. 1

З’ясувати, чим схожі і чим відрізняються ці приклади.

Доцільно за даними прикладами (4 + 3 і 4 • 3) зробити малюнки, знайти результати і порівняти приклади.

Корисні вправи з рівностями і нерівностями, наприклад: Порівняйте вирази і поставте знак «>», «<», «=»:

18 • 2 * 18 • 3

4 + 4 + 4 * 4 • 2

3 • 4 * 2 • 4

4 • 7 + 4 * 4 • 9

Наведемо пояснення учня під час виконання останнього завдання: зліва додали сім четвірок та ще додали одну – всього стало 8 четвірок, а справа їх 9. Зліва четвірок менше, ніж справа, отже, вираз зліва менший; поставимо знак «<».

Під час виконання вправ треба звертати увагу учнів на прийнятий у нашій країні порядок розміщення множників у записі множення: на першому місці пишуть число, яке береться доданком, а на другому – число, яке показує, скільки береться однакових доданків.

Зауважимо, що для вправ можна використовувати приклади не лише з одноцифровими множниками (4 • 3), а й з двоцифровими (12 • 3). Це роблять для того, щоб учні на цьому ступені практично користувалися відомим їм взаємозв’язком між множенням і додаванням, вправлялися у виконанні різних випадків додавання.

На цьому етапі учні не повинні запам’ятовувати напам’ять результати множення.

Конкретний зміст ділення розкривають у процесі розв’язування задач спочатку на ділення на вміщення, а потім на рівні частини.

У зв’язку з цим учні повинні вміти виконувати за умовою задачі операцію розбиття множини на ряд рівночисельних множин; розуміти, що з цією операцією пов’язана дія ділення; навчитися записувати розв’язування задач за допомогою цієї дії.

Учні II класу ознайомлюються з назвами компонентів і результатів дій множення і ділення: перший множник, другий множник, добуток, пізніше – ділене, дільник, частка. Тут же діти дізнаються, що терміни «добуток» і «частка» означають не лише результат дії, а й відповідний вираз, наприклад: 4 • 3 і 20: 5.

Наступний крок у вивченні дії множення – розкриття переставної властивості множення. Знати цю властивість насамперед для засвоєння дії множення, а крім того, знання цієї властивості дає можливість майже вдвічі скоротити кількість випадків, які треба вивчити напам’ять. Замість двох випадків (8 • 3 і 3 • 8) учні запам’ятовують лише один.

Переставну властивість множення учні можуть «відкрити» самостійно, використовуючи наочні посібники у вигляді рядів кліток (кружків, ґудзиків, зірочок тощо). Наприклад, діти креслять прямокутник, ділять його на квадрати (рис. 2).

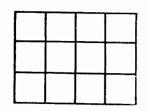
Рис. 2

Їм пропонують дізнатися двома способами, скільки всього буде квадратів (4 • 3 = 12 і 3 • 4 = 12). Порівнявши ці приклади, учні помічають, що множники однакові, тільки помінялися місцями, добутки однакові.

Після виконання кількох аналогічних вправ учні формулюють властивість: «Від переставляння множників добуток не змінюється».

Засвоєнню переставної властивості множення допомагають вправи, аналогічні таким: обчисліть результат другого прикладу, користуючись результатом першого: 7 • 6 = 42 і 6 • 7 =…; порівняйте вирази і поставте замість зірочки знак «>», «<» або «=»: 6 • 3 * 3 • 6; вставте замість зірочки пропущений знак дії: 7 * 2 = 2 • 7; вставте пропущене число: 2 • 3 = 3 • . Виконуючи кожну вправу, учні повинні порівняти вирази і помітити, що в добутках множники однакові, тільки переставлені, отже, добутки однакові. На цій основі добирають знак дії або число.

У II класі переставну властивість множення записують у загальному вигляді за допомогою букв: а • b – b • а.

Щоб створити кращі умови для вивчення табличних випадків множення і ділення, розкривають зв’язок між компонентами і результатом дії множення, а також узагальнюють два види ділення. Виходячи з цих знань, учні на підставі кожного випадку множення можуть дістати відповідні випадки ділення: якщо 7 • 3 = 21, то 21: 7 = 3 і 21: 3 = 7.

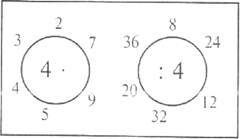
Зв’язок між компонентами і результатом дії множення розкривають за допомогою наочних посібників. Учням пропонують скласти приклад на множення за рисунком (рис. 3).

Рис. 3

Учні складають приклад: 4 • 3 = 12. Назвіть перший множник. (4.) Назвіть другий множник. (3.) Назвіть добуток. (12.) Користуючись цим рисунком, складіть два приклади на ділення (12: 4 = 3, 12: 3 = 4). Дістаємо запис:

4 • 3 = 12

12: 4 = 3

12: 3= 4

Порівняйте приклади на ділення з прикладом на множення. Як дістали другий множник 3? (Добуток 12 поділили на перший множник 4.) Як дістали перший множник 4? (Добуток 12 поділили на другий множник 3.)

Виконавши кілька аналогічних вправ, учні роблять висновок: якщо добуток двох чисел поділити на перший множник, то дістанемо другий множник, а якщо добуток двох чисел поділити на другий множник, то дістанемо перший множник.

Пізніше ці два висновки об’єднують в один: якщо добуток двох чисел поділити на один з множників, то дістанемо другий множник.

Щоб добитися засвоєння учнями зв’язку між добутком і множником, пропонують такі вправи.

Складіть за прикладом 5 • 3 = 15 два приклади на ділення. Учні міркують: якщо добуток 15 поділимо на перший множник 5, то дістанемо другий множник 3, а якщо добуток 15 поділимо на другий множник 3, то дістанемо перший множник 5.

Аналогічно міркують учні під час виконання вправи на складання прикладів на множення і ділення, використовуючи задані числа, наприклад: 2, 5, 10 (2 • 5=10, 10: 2 = 5, 10: 5 = 2).

Корисно запропонувати розв’язати такі стовпчики прикладів:

3 • 5

7 • 2

6 • 4

5 • 3

2 • 7

4 • 6

15: 3

14: 7

24: 6

15: 5

14: 2

24: 4

Учні розв’язують приклади першого стовпчика, користуючись додаванням. Потім визначають результат відповідного прикладу з другого стовпчика, використовуючи переставну властивість множення, нарешті, розв’язують приклади третього і четвертого стовпчиків, користуючись знанням зв’язку між множниками і добутком.

Особливу увагу треба приділити вправам на знаходження результату ділення за відомим добутком. Нехай треба розв’язати приклад на ділення: 24: 6, якщо дано приклад на множення: 6 • 4=24. Учень міркує: 24 – добуток, а 6 – перший множник; якщо добуток 24 поділити на перший множник 6, то дістанемо другий множник 4.

Пізніше аналогічно розв’язують питання про знаходження невідомого діленого і дільника.

Далі доцільно розглянути питання про узагальнення двох видів ділення.

У зв’язку з тим що конкретний зміст дії ділення розкривали за допомогою розв’язування простих задач на ділення на вміщення і на рівні частини, в учнів може виникнути неправильне уявлення про дію ділення: ніби існує дві різні дії ділення. Тому дуже важливо показати дітям, що незалежно від того, чи ділимо на вміщення чи на рівні частини, дістанемо однакові частки, якщо ділимо ті самі числа.

До узагальнення двох видів ділення учнів підводять за допомогою порівняння розв’язувань пар простих задач з однаковими числовими даними на ділення на вміщення і на ділення на рівні частини. Наприклад, пропонують розв’язати таку пару задач:

1) 12 яблук розклали на 4 блюдечка порівну. Скільки яблук у кожному блюдечку?

2) 12 яблук розклали в блюдечка по 4 яблука. Скільки потрібно було блюдечок?

Записавши розв’язання кожної задачі і відповіді до них, встановлюють схоже і різне в задачах, розв’язаннях і відповідях. Особливу увагу звертають на однакові дані числа 12 і 4 і на однакові числа у відповідях 3. Виконавши кілька аналогічних вправ, учні з’ясовують, що в обох випадках при однакових ділених і однакових дільниках дістаємо однакові частки.

На цьому самому етапі вивчають прийоми для випадків множення і ділення з числами 1 і 10. Розкриваючи прийоми, учні застосовуватимуть тільки що здобуті знання, а отже, краще їх засвоять. Крім того, вони опанують прийоми, на основі яких швидко знаходитимуть результати, тому відпаде потреба їх заучувати.

Спочатку розглядають випадок множення одиниці на числа, більші за одиницю. Учні розв’язують ряд прикладів, знаходять результат додаванням: 1 • 2 = 1 + 1 = 2; 1 • 3 = 1 + 1 + 1 = 3 і т. д. Потім, порівнявши в кожному випадку результат з множниками, вони приходять до висновку: при множенні одиниці на будь-яке число виходить те число, на яке множили. Надалі аналогічні приклади розв’язують на основі цього правила.

Потім вводять правило множення на 1: при множенні будь-якого числа на 1 виходить те число, яке множили, наприклад: 4 • 1 = 4, 12 • 1 = 12, а • 1 = а. Тут не можна використати прийом заміни добутку сумою, через де не можна спиратися і на переставляння множників, тому треба просто повідомити дітям це правило і надалі використовувати його під час обчислення.

Ділення на число, яке дорівнює діленому (3: 3 = 1), розкривають на основі конкретного змісту ділення: якщо, наприклад, 3 олівці розкласти в 3 коробки порівну, то в кожній коробці буде по одному олівцю. Міркуючи так, учні розв’язують кілька аналогічних прикладів: 4: 4 = 1, 6: 6 = 1 і т. д. При цьому помічають, що при діленні на число, яке дорівнює діленому, у частці дістаємо 1.

Ділення на 1 вводять на основі зв’язку між компонентами і результатом дії множення: знаючи, що 1 • 4 = 4, знайдемо, що 4: 1 = 4. Розв’язавши так ряд прикладів і порівнявши їх між собою, учні роблять висновок: при діленні будь-якого числа на одиницю в частці дістаємо те саме число. Цим висновком вони користуються надалі під час обчислень.

При множенні 10 на одноцифрові числа учні користуються прийомом: щоб помножити 10 на 2, можна 1 дес. помножити на 2, буде 2 дес., або 20. Множачи на 10, діти використовують переставну властивість множення: щоб 2 помножити на 10, можна 10 помножити на 2, буде 2 дес., або 20. При діленні використовують знання зв’язку між компонентами і результатом дії множення: щоб 20 поділити на 10, треба підібрати таке число, при множенні якого на 10 буде 20; це 2; отже, 20: 2 = 10. Так само знаходимо, що 20: 2 = 10.

Знання про дії множення і ділення, а також уміння, набуті учнями на першому етапі, є основою вивчення на другому етапі табличних випадків множення і відповідних випадків ділення.

Табличне множення і ділення вивчають одночасно, тобто з кожного випадку множення дістають відповідні випадки ділення: якщо 5 • 3 = 15, то 15: 5 = 3 і 15: 3 = 5. Основою для цього є знання учнями зв’язку між компонентами і результатом дії множення.

Спочатку розглядають усі табличні випадки множення і ділення з числом 2, потім 3, 4 і т. д.

Табличні випадки множення і ділення з кожним числом вивчають приблизно за одним планом.

Насамперед складають таблицю множення за сталим першим чи другим множником. Якщо скласти таблицю за сталим першим множником (2 • 2, 2 • 3, 2 • 4), то учні легко знаходитимуть результат наступного прикладу, користуючись результатом попереднього (2 • 4 = 2 • 3 + 2), але в цьому випадку в деяких сумах буде багато доданків (2 • 9 – дев’ять доданків). Якщо складати таблицю за сталим другим множником (2 • 2, 3 • 2, 4 • 2 і т. д.), доданків буде менше. Ця таблиця зручніша для запам’ятання, зате тут важче знаходити результат: доданки кожного наступного прикладу інші (2 • 2 = 2 + 2, 3 • 2 = = 3 + 3, 4 • 2 = 4 + 4,…); щоб знайти результат наступного прикладу, користуючись попередніми, доведеться міркувати так:

4 • 2 = 3 • 2 + 2, 5 • 2 = 4 • 2 + 2.

Вчитель може взяти будь-який з цих двох варіантів.

Ми візьмемо спочатку таблицю за сталим першим множником. Щоб знайти результат, використовують різні прийоми: добуток замінюють сумою

(2 • 3 = 2 + 2 + 2 = 6); до результату попереднього прикладу з таблиці додають відповідне число: 5 помножити на 3, буде 15, а під час множення 5 на 4 (на одну п’ятірку більше) можна результат обчислити так: 15 + 5 = 20; або від відомого результату віднімають відповідне число: учні знають, що 8 • 10 = 80, 8 • 9 (на одну вісімку менше), тому результат можна обчислити так: 80 – 8 = 72; використовують переставляння множників (2 • 5 = 5 • 2).

Якщо таблицю складено за сталим першим множником, то з кожного прикладу на множення учні складають ще один приклад на множення (переставляють множники) і два приклади на ділення (на основі зв’язку між компонентами і результатом множення), наприклад:

І II III IV

2 • 2 = 4

2 • 3 = 6

2 • 4 = 8

2 • 5 = 10

3 • 2 = 6

4 • 2 = 8

5 • 2 = 10

4: 2 = 2

6: 2 = 3

8: 2 = 4

10: 2 = 5

6: 3 = 2

8: 4 = 2

10: 5 = 2 і т. д.

Кожну таблицю множення за сталим першим множником складають, починаючи з випадку однакових множників (2 • 2, 3 • 3, 4 • 4 і т. д.), оскільки випадки, які передують цим, вже були розглянуті раніше (наприклад, випадок 3 • 2 був наведений у таблиці з числом 2 і тому в таблиці з числом 3 його не вивчають).

Приклади на множення читають по-різному: по 5 узяти 2 рази, буде 10; 5 помножити на 2, буде 10; добуток чисел 5 і 2 дорівнює 10; перший множник 5, другий 2, добуток 10; двічі по п’ять – десять; пізніше: 5 збільшити в 2 рази, буде 10.

Приклади на ділення читають так: 6 поділити на 2, буде 3. Можна читати приклади на ділення інакше, використовуючи назви компонентів і результату: частка чисел 6 і 2 дорівнює 3; ділене 6, дільник 2, частка 3, а пізніше можна читати так: 6 зменшити в 2 рази, буде 3.

Розглянувши на одному уроці всі випадки множення і ділення з яким-небудь числом, треба виділити ті з них, які слід вивчити напам’ять. Корисно ці випадки виписати кожному учневі на окремий аркуш.

Розглянемо методику роботи з вивчення таблиці множення чотирьох і відповідних випадків ділення.

До підготовчої роботи можна включити вправи на знаходження невідомого множника (х • 2 = 8; 3 • а = 15), можна повторити таблицю множення двох і трьох і відповідні випадки ділення треба повторити також усі відомі дітям випадки множення і ділення з числом 4 (4 • 1, 4 • 2, 4 • 3, 4 • 10 і відповідні випадки множення та ділення).

Потім переходять до складання таблиці множення чотирьох за сталим першим множником.

Ви вже знаєте таблицю множення двох і трьох, а сьогодні складемо і вивчатимемо таблицю множення чотирьох.

Учитель відкриває заздалегідь записану на дошці таблицю множення чотирьох (4 • 4, 4 • 5,…, 4 • 9) і пропонує переписати її в зошит.

– Обчисліть перший добуток. (16.)

– Як обчислювали? (4+4+4+4 = 16.)

– Запишіть обчислення додаванням внизу під таблицею множення. (Учні записують у зошитах, а вчитель – на дошці.)

– Позначте добуток цих чисел, використовуючи квадрат з кутником (рис. 4). (Учні показують 4 ряди квадратів по 4 квадрати в кожному.)

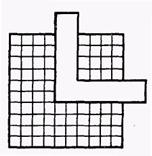
Рис. 4

– Отже, скільки буде, якщо 4 помножити на 4? (16.)

– Запишіть у таблицю множення.

– Тепер обчислимо такий добуток: 4 • 5. Як ви позначите його на квадратах? (Діти показують 5 рядів квадратів, по 4 квадрати в кожному.)

– Скільки всього квадратів? (20.)

– Як ви дізналися? (4 + 4 + 4 + 4 + 4 = 20.)

– Запишіть цю суму під першою.

– Як можна обчислити другу суму, користуючись результатом

першої? (16 + 4 = 20.)‘

– Як інакше можна обчислити результат? (Переставити місцями множники: 5 • 4 – це 5 + 5 + 5 + 5 = 20.)

– Скільки ж буде, якщо 4 помножити на 5? (20.)

– Запишемо. Який наступний приклад розв’язуватимемо? (4 помножити на 6.)

– Розв’яжіть і назвіть результат. (24.)

– Як обчислювали? (4 + 4 + 4 + 4 + 4 + 4 = 24.)

– Запишемо. Як інакше можна розв’язати цей приклад? (Переставити місцями множники: 6 • 4 – це 6 + 6 + 6 + 6 = 24 або додати до попереднього результату, до 20, число 4.) Можна ще й так обчислити: 4 + 4 + 4 (підкреслити) і ще 4 + 4 + 4 (підкреслити), 12 + 12 = 24, тобто можна згрупувати доданки.

Так само розглядають інші випадки: деякі добутки діти ілюструють на своїх посібниках, знаходять кількість квадратів додаванням, записують суму, з’ясовують, якими ще способами можна обчислити результат (додати 4 до попереднього результату, згрупувати доданки, переставити множники місцями).

Як тільки будуть розглянуті всі випадки, учні читають таблицю множення.

– Ми записали всі випадки множення чотирьох. Скажіть, які ще приклади на множення можна скласти з такими самими результатами. (Переставити місцями множники.)

Поряд із таблицею множення чотирьох учні самостійно записують таблицю множення на 4 і читають її по-різному.

– Які приклади на ділення можна скласти за цими прикладами на множення? Почніть з другого прикладу. (20: 4 = 5, 20: 5 = 4.)

– Запишіть це.

– Як ви визначили? (Добуток ділили на один із множників, дістали другий множник.)

Учні складають до кожного прикладу на множення два приклади на ділення і записують їх. Останніми складають приклади до випадку 4 • 4; тут дістають однакові приклади на ділення.

Корисно запропонувати учням розглянути всі приклади першої таблиці і сказати, що цікавого вони помітили. Діти повинні відповісти, що перші множники однакові, другі множники збільшуються на одиницю, а добутки – на 4 одиниці. Так само порівнюють приклади й інших стовпчиків.

Таблицю множення чотирьох треба вивчити напам’ять, щоб щоразу не обчислювати результат. Обведіть її червоним олівцем, а вдома випишіть цю таблицю на окремий аркуш.

На дошці вчитель витирає результати всіх прикладів і пропонує закрити зошити: «Повторимо таблицю множення чотирьох, множення на 4 і всі випадки ділення».

Учитель викликає до дошки чотирьох учнів, кожний з яких називає приклад (почати краще з випадку 4 • 5):

Перший учень. 4 помножити на 5, буде 20.

Другий учень. 5 помножити на 4, буде також 20.

Третій учень. 20 поділити на 4, буде 5.

Четвертий учень. 20 поділити на 5, буде 4.

Так повторюють усі випадки.

Як було вже зазначено, аналогічно працюють над іншими таблицями. Кількість нових випадків у кожній наступній таблиці зменшується. Учні від таблиці до таблиці виявляють більше самостійності в складанні їх. Вони швидко помічають, що в кожній. таблиці множення за сталим першим множником першим береться приклад з однаковими множниками, що в кожному наступному прикладі на одиницю більший другий множник (2 • 3; 2 • 4). Усе це допомагає учням самостійно скласти черговий новий приклад і розв’язати його. Вже при складанні таблиці множення чотирьох або п’яти можна запропонувати учням самостійно назвати перший, другий і т. д. приклади таблиці по порядку.

Під час вивчення таблиць і пізніше треба приділяти велику увагу вправам на запам’ятовування табличних результатів: скласти чотири приклади на множення і ділення з однаковими числами (4 • 3 = 12, 3 • 4 = 12, 12: 4 = 3, 12: 3 = 4), повторити таблиці по порядку і в розбивку, скласти напам’ять таблицю множення двох або на 2, трьох або на 3 і т. д., замінити число (24) добутком відповідних множників (8 • 3, 6 • 4), відгадати задумане число (якщо його множили на 8 і дістали 72). Корисно з цією метою разом з учнями скласти таблицю множення Піфагора і навчити їх нею користуватися.

Зауважимо, що заучують напам’ять лише результати множення, а відповідні випадки ділення учні повинні вміти швидко знаходити, користуючись таблицею множення. Знаючи, наприклад, що 7 • 8 = 56, вони повинні швидко розв’язувати приклади: 56: 7 = 8 і 56: 8 = 7. Під час тренування учні повинні міцно запам’ятати трійки чисел, наприклад: 3, 7, 21; 9, 8, 72 і т. д.

Для запам’ятовування табличних результатів потрібен деякий час, тому вчитель як у II, так і в III класі повинен систематично давати вправи на запам’ятовування таблиці множення.

Вивчивши всі таблиці множення, розглядають випадки множення і ділення з нулем.

Спочатку вводять випадок множення нуля на будь-яке число (0 • 5, 0 • 2, 0 • 7). Результат учні знаходять додаванням:

(0 • 2 = 0 + 0 = 0, 0 • 3 = 0 + 0 + 0 = 0). Розв’язавши ряд аналогічних прикладів, учні помічають, що при множенні нуля на будь-яке число буде нуль. Цим правилом вони надалі й керуються.

Якщо другий множник дорівнює нулю, то результат не можна знайти додаванням, не можна використати і переставлення множників, бо це нова область чисел, в якій переставна властивість множення не розкривалась. Тому друге правило: «Добуток будь-якого числа на нуль вважають таким, що дорівнює нулю» – учитель просто повідомляє дітям. Потім обидва ці правила застосовують у процесі виконання різних вправ на обчислення.

Ділення нуля на будь-яке число, яке не дорівнює нулю (0: 6), розглядають на основі зв’язку між компонентами і результатом множення. Учні міркують так: щоб 0 поділити на 6, треба знайти число, при множенні якого на 6 буде 0. Це нуль, бо 0 • 6 = 0. Отже, 0: 6=0. Внаслідок розв’язування ряду аналогічних прикладів учні помічають, що при діленні нуля на будь-яке число, яке не дорівнює нулю, частка дорівнює нулю. Надалі учні користуються цим правилом.

Як відомо, ділити на нуль не можна. Цей факт повідомляють дітям і пояснюють на прикладі: не можна 8 поділити на 0, бо немає такого числа, при множенні якого на 0 було б 8.

Позатабличне множення і ділення. Випадки позатабличного множення і ділення вивчають у такому порядку. Спочатку розглядають властивості множення числа на суму і суми на число. Потім вивчають множення і ділення чисел, які закінчуються нулем, вводять множення двоцифрового числа на одноцифрове і множення одноцифрового числа на двоцифрове. Далі вводять властивість ділення суми на число, на основі якого розкривають прийом ділення двоцифрового числа на одноцифрове. Нарешті, розглядають ділення двоцифрового числа на двоцифрове. Під час вивчення цієї теми вводять перевірку множення і ділення.

Розглянемо спочатку методику роботи над властивостями добутку і частки, а потім перейдемо до викладу методики вивчення обчислювальних прийомів.

Методика вивчення властивостей множення і ділення суми на число і множення числа на суму подібна до тієї, яку вже використовували в І класі під час розкриття властивостей додавання числа до суми, віднімання числа від суми тощо. Спочатку виконують підготовчу роботу, потім учні ознайомлюються з властивістю, після чого застосовують її під час виконання різних вправ. Пізніше, користуючись властивістю, розкривають прийоми позатабличного множення і ділення.

Підготовкою до вивчення властивості множення числа на суму буде добре знання конкретного змісту дії множення і правил про порядок виконання арифметичних дій у виразах без дужок.

Під час ознайомлення з властивістю множення числа на суму можна використати такий прийом. Учні читають вираз 4 • (3+2) і обчислюють його значення вже відомим способом:

4 • (3 + 2) = 4 • 5 = 20.

Цей спосіб корисно ще раз пояснити за допомогою такого рисунка (рис. 5).

Рис. 5

Користуючись цим рисунком, учні можуть відшукати й інший спосіб: спочатку дізнаємось, скільки чорних кружечків (4 • 3), потім скільки білих кружечків (4 • 2), нарешті, скільки всього кружечків (4 • 3 + 4 • 2).

Запис:

4 • (3 + 2) = 4 • 3 + 4 • 2 = 20.

У цьому випадку множили на кожний доданок і знайдені результати додали. Порівнявши знайдені результати розв’язання прикладу різними способами, учні помічають, що вони однакові.

Потім учні розв’язують двома способами приклади виду: 8 • (2+4), 4 • (6 + 4) і переконуються, що кожного разу дістають однакові результати. На цій підставі вони роблять висновок, що множити число на суму можна різними способами, дістаючи однакові результати: можна обчислити суму і множити число на знайдений результат, а можна множити число на кожний доданок і знайдені результати додати.

Для засвоєння цієї властивості учні виконують різні вправи:

1) Обчисліть результат різними способами:

10 • (6 + 2) = 10 • 8 = 80

10 • (6 + 2) = 10 • 6 + 10 • 2 = 80

2) Обчисліть результат найзручнішим способом:

8 • (10 + 2) = 8 • 10 + 8 • 2 = 96

9 • (6 + 4) = 9 • 10 = 90

Через кілька уроків треба ввести обернені вправи, в яких суму добутків треба замінити добутком числа на суму, наприклад: 6 • 4 + 6 • 5 = 6 • (4 + 5).

Міркування: число 6 береться доданком 4 рази, а потім це саме число 6 береться доданком ще 5 раз, всього (4 + 5) раз, можна записати:

6 • 4 + 6 • 5 = 6 • (4 + 5).

Увагу учнів треба звернути на умову, при якій така заміна можлива, тобто на рівність перших множників. Тому корисно пропонувати і такі добутки, в яких перші множники різні, наприклад: 4 • 3 + 5 • 6. Діти повинні впевнитись, що таку суму двох добутків не можна замінити добутком числа на суму.

Для цього розглядають задачі, запис розв’язання яких у вигляді виразу є сумою двох добутків з однаковими або різними множниками.

Аналогічно вводять інші властивості – множення суми на число і ділення суми на число.

Зазначимо, що учні, ознайомившись із властивостями множення числа на суму і суми на число, іноді плутають їх з раніше засвоєними властивостями додавання суми до числа і числа до суми, наприклад: (10 + 6) • 4 = 10 • 4 + 6. Тут учні множили на число 4 тільки перший доданок, а потім додали другий, тобто вони робили так само, як і додаючи число до суми. Тому корисно вводити спеціальні вправи, які запобігли б плутанню вивчених властивостей. Так, можна пропонувати розв’язування і наступне порівняння пар прикладів виду:

(6 + 4) • 3 і (6 + 4) + 3; доцільно включати вправи, в яких треба закінчити запис, наприклад:

8 • (10 + 2) = 8 • 10 +… і 8 + (10 + 2) = (8+ 10) +… і т. д.

Засвоєння властивостей множення числа на суму, множення і ділення суми на число безпосередньо підводить учнів до розкриття прийомів позатабличного множення і ділення. До того ж треба врахувати, що під час вивчення додавання і віднімання в межах 100 в учнів уже сформувалося вміння користуватися властивостями арифметичних дій для обґрунтування обчислювальних прийомів додавання і віднімання, тому, вводячи прийоми позатабличного множення і ділення, треба надати учням більше самостійності.

Спочатку вводять прийоми для випадків множення і ділення чисел, які закінчуються нулем. Розв’язування таких прикладів зводиться до множення і ділення одноцифрових чисел, які визначають число десятків. Наприклад:

 

20 • 3

2 дес. • 3 = 6 дес.

20 • 3 = 60

80: 4

8 дес.: 4 = 2 дес.

80: 4 = 20

При множенні одноцифрових чисел на круглі двоцифрові числа використовують прийом переставляння множників (4 • 20 = 20 • 4).

Круглі двоцифрові числа на круглі двоцифрові ділять способом добору частки на підставі зв’язку між компонентами і результатом множення. Наприклад, щоб 60 поділити на 20, треба знайти таке число, при множенні якого на 20 буде 60. Спочатку пробуємо: 2 – мало, 3 – підходить, бо 20 • 3 = 60. Отже, 60: 20 = 3.

Після вивчення властивості множення числа на суму і суми на число вводять прийоми, які ґрунтуються на цих властивостях. Прийом множення двоцифрового числа на одноцифрове не потребує особливих роз’яснень. Учні можуть самостійно знайти спосіб розв’язування нових прикладів: 12 • 4, 24 • 3 або ж пояснити хід розв’язування нового прикладу за розгорнутим записом його розв’язання:

12 • 3 = (10 + 2) • 3 = 10 • 3 + 2 • 3 = 36.

Учні мають самостійно виділити три основні етапи, з яких складається розв’язання прикладів: замінити перший множник сумою розрядних доданків, прочитати знайдений вираз (10 + 2) • 3 і обчислити добуток зручним способом: помножити на число кожний доданок окремо і знайдені доданки додати.

Важливо своєчасно скоротити пояснення: 12 • 3, десять помножити на три, буде 30; 2 помножити на 3, буде 6; до 30 додати 6, буде 36. У необхідних випадках можна знову звернутися до докладного пояснення.

Під час множення одноцифрового числа на двоцифрове використовують властивість множення числа на суму, наприклад:

6 • 12 = 6 • (10 + 2) = 6 • 10 + 12 = 72.

Можна використати і переставну властивість множення:

6 • 12 = 12 • 6 =72.

Корисно порівняти множення двоцифрового числа на одноцифрове і множення одноцифрового числа на двоцифрове, звернувши увагу учнів на велику схожість цих випадків множення. Доцільно також порівняти прийоми множення і додавання, наприклад:

3 • 14 = 3 • (10 + 4) = 3 • 10 + 3 • 4 = 42

30 + 14 = 30 + (10 + 4) = 30 + 10 + 4 = 44

Під час діл єн н я двоцифрового числа на одноцифрове користуються властивістю ділення суми на число. Цей випадок позатабличного ділення учні засвоюють важче, ніж множення двоцифрового числа на одноцифрове. Справа ускладнюється тим, що при діленні двоцифрового числа на одноцифрове трапляються різні групи прикладів:

1) 46: 2 = (40 + 6): 2 =40: 2 + 6: 2 = 20 + 3 = 23

2) 50: 2 = (40 + 10): 2 = 40: 2 + 10: 2 = 20 + 5 = 25

3) 72: 6 = (60 + 12): 6 = 60: 6 + 12: 6 = 10 + 2 = 12

У першому прикладі (46: 2) доводиться ділене замінювати сумою розрядних доданків (40 + 6), у другому (50: 2) – сумою зручних доданків, якими будуть круглі числа (40 + 10), у третьому (72: 6) – сумою двох чисел, одне з яких кругле число, а друге – двоцифрове (60 + 12). У всіх прикладах задані доданки будуть зручними в тому розумінні, що від ділення їх на заданий дільник дістаємо розрядні доданки частки. Учням буває важко знайти саме зручні доданки.

Щоб підготуватись до розкриття нового прийому, корисно пропонувати такі вправи: виділяти круглі числа до 100, які учні вже вміють ділити на 2 (10, 20, 40, 60, 80), на 3 (30, 60, 90), на 4 (40, 80) і т. д.; записувати різними способами числа у вигляді суми двох доданків, кожний з яких ділиться на задане число без остачі: наприклад, 24 можна замінити такою сумою, кожний доданок якої ділиться на 2: 20 + 4, 12 + 12, 10 + 14 і т. д.; розв’язувати різними способами приклади виду: (18 + 45): 9.

Після підготовчої роботи спочатку розглядають приклади першої групи, під час розв’язування яких доводиться ділене замінювати сумою розрядних доданків, наприклад: 36: 3= (30 + 6): 3 = 30: 3 + 6: 3 = 12. Цей матеріал для дітей легкий, а тому вони можуть самостійно встановити спосіб розв’язування нових прикладів або пояснити за розгорнутим записом їх розв’язання.

Потім вивчають приклади другої групи, під час розв’язування яких доводиться ділене замінювати сумою зручних доданків, наприклад:

30: 2 = (20 + 10): 2 = 20: 2 + 10: 2 = 15

78: 6 = (60 + 18): 6 = 60: 6 + 18: 6 = 13

Тут зручні доданки знайти важче, ніж у прикладах першої групи. Тому треба приділити велику увагу заміні діленого сумою зручних доданків і вибору найзручнішого способу. Так, приклад 42: 3 можна розв’язати різними способами:

42: 3 = (30 + 12): 3 = 30: 3 + 12: 3 = 14

42: 3 == (27 + 15): 3 = 27: 3 + 15: 3 = 14

42: 3 = (24 + 18): 3 = 24: 3 + 18: 3 = 14

42: 3 = (36 + 6): 3 = 36: 3 + 6: 3 = 14 і т. д.

До найзручнішого способу тут треба віднести перший спосіб, бо при діленні зручних доданків (30 і 12) дістаємо розрядні доданки частки (10 + 4 = 14).

Особливо важкими для учнів є приклади виду: 96: 4. У таких випадках доцільно замінити ділене сумою таких зручних доданків, перший з яких виражає найбільше число десятків, що діляться на дільник: 96: 4= (80 + 16): 4.

До позатабличного ділення належить також ділення двоцифрового числа на двоцифрове. У цьому випадку, як і при діленні на круглі десятки, використовують спосіб добору частки, який ґрунтується на зв’язку між компонентами і результатом дії множення: добирають частку, а потім її перевіряють множенням. Так, при розв’язуванні прикладу 81: 27 ставлять запитання: на яке число треба помножити 27, щоб дістати 81? (На число 3.) Отже, 81: 27 = 3.

Під час ділення двоцифрового числа на двоцифрове слід показати дітям деякі прийоми добору частки. Учні спочатку знаходять частку повільно, беруть числа по порядку: 2, 3, 4 і т. д. Поступово число проб скорочуватиметься, якщо вчитель навчатиме дітей добирати частку. Так, при діленні 77 на 11 немає потреби брати багато чисел. Тут треба уважно подивитися на ділене і дільник, і стане зрозуміло, що в частці буде 7. При діленні 90 на 15 також після першої проби (15 • 2=30) корисно порівняти числа 30 і 90. (Якщо 2 рази взяти по 15, то буде 30, а нам треба, щоб було 90. Скільки ж разів треба взяти по 15? Два рази, ще два рази і ще два рази, а всього 6 раз.

Перевіримо: 15 • 6 = 90, отже, 90: 15 = 6).

Для формування навички добору частки велике значення мають також вправи тренувального характеру і знання напам’ять деяких випадків позатабличного множення.

У процесі вивчення позатабличного множення і ділення вводять перевірку множення і ділення.

Ділення учні перевіряють множенням. Візьмемо приклад: 54: 3 = 18. Під час перевірки множать знайдену частку на дільник: 18 • 3 = 54. Дістали ділене. Якщо під час множення частки на дільник не дістанемо діленого, то, отже, в обчисленнях допущено помилку.

Множення перевіряють діленням. Візьмемо приклад: 24 • 4 = 96. Для перевірки ділимо добуток на другий множник (або перший): 96: 4 = 24 (96: 24 = 4). Дістали перший множник (другий). Якщо під час ділення добутку на один з двох множників не дістанемо другого множника, то, отже, в обчисленнях допущено помилку.

Ці знання учнів застосовують у різних вправах: при виконанні ділення (множення) і перевірки розв’язку множенням (діленням).

 

2.2 Конспекти уроків на засвоєння таблиць множення та ділення

 

Тема: Таблиця множення числа 6. Знаходження значень виразів з буквою, що повторюється.

Мета: ознайомити учнів з таблицею множення числа 6; удосконалювати вміння учнів обчислювати значення виразів з буквою.

І. Контроль, корекція і закріплення знань.

Усні обчислення.