Понятие «натуральное число», свойства натуральных чисел

1.3.     Понятие «натуральное число», свойства натуральных чисел

Число является одним из основных понятий математики. Понятие числа развивалось в тесной связи с изучением величин; эта связь сохраняется и теперь. Во всех разделах современной математики приходится рассматривать разные величины и пользоваться числами

Существует большое количество определений понятию «число».

Первое научное определение числа дал Эвклид в своих «Началах», которое он, очевидно, унаследовал от своего соотечественника Эвдокса Книдского (около 408 – около 355 гг. до н. э.): «Единица есть то, в соответствии с чем каждая из существующих вещей называется одной. Число есть множество, сложенное из единиц». Считается, что термин «натуральное число» впервые применил римский государственный деятель, философ, автор трудов по математике и теории музыки Боэций (480 – 524 гг.), но еще греческий математик Никомах из Геразы говорил о натуральном, то есть природном ряде чисел [20, с.199].

Понятием «натуральное число» в современном его понимании последовательно пользовался выдающийся французский математик, философ-просветитель Даламбер.

Натура́льные чи́сла — числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления) предметов [24, с.67]. Существуют два подхода к определению натуральных чисел, отличающиеся причислением нуля к натуральным числам. Соответственно, натуральные числа определяются как:

- числа, используемые при перечислении (нумеровании) предметов: 1, 2, 3, … (первый, второй, третий и т. д.). Это определение общепринято в большинстве стран, в том числе и в России.

- числа, используемые при обозначении количества предметов: 0, 1, 2, … (нет предметов, один предмет, два предмета и т. д.). Это определение было популяризовано в трудах Бурбаки, где натуральные числа определяются как мощности конечных множеств.

Отрицательные и нецелые числа натуральными не являются.

Натуральные числа имеют две основные функции:

q   характеристика количества предметов;

q   характеристика порядка предметов, размещенных в ряд.

В соответствии с этими функциями возникли понятия порядкового числа (первый, второй и т.д.) и количественного числа (один, два и т.д.).

Долго и трудно человечество добиралось до 1-го уровня обобщения чисел. Сто веков понадобилось, чтобы выстроить ряд самых коротких натуральных чисел от единицы до бесконечности:1, 2, … ∞. Натуральных потому, что ими обозначались (моделировались) реальные неделимые объекты: люди, животные, вещи…

Свойства чисел натурального ряда, а также производных от них находятся в различной периодической зависимости от порядковых номеров чисел.

Основные свойства натуральных чисел:

Коммутативность сложения.

Коммутативность умножения.

Ассоциативность сложения.

Ассоциативность умножения.

Дистрибутивность умножения относительно сложения.

Свойства сложения и умножения натуральных чисел:

a + b = b + a - переместительное свойство сложения

(a + b) + c = a + (b +c) - сочетательное свойство сложения

ab = ba - переместительное свойство умножения

(ab)c = a(bc) - сочетательное свойство умножения

a(b + c) = ab + ac - распределительное свойство умножения относительно сложения

Результатом сложения и умножение двух натуральных чисел всегда является натуральное число.

Если m, n, k натуральные числа, то при m - n = k говорят, что m - уменьшаемое, n - вычитаемое, k - разность; m : n = k говорят, что m - делимое, n - делитель, k - частное.

Признаки делимости натуральных чисел .

Если каждое слагаемое делится на некоторое число, то и сумма делится на это число.

Если в произведении хотя бы один из множителей делится на некоторое число, то и произведение делится на это число.

Натуральное число делится на 2 тогда и только тогда, когда последняя цифра делится на 2.

Натуральное число делится на 5 тогда и только тогда , когда его последняя цифра либо 0, либо 5.

Натуральное число делится на 10 тогда и только тогда , когда его последняя цифра 0.

Натуральное число, содержащее не менее трех цифр, делится на 4 тогда и только тогда, когда делится на 4 двузначное число, образованное последними двумя цифрами заданного числа. Натуральное число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3. Натуральное число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9 [5, с.174 ].

Таким образом, натура́льные чи́сла — числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления). Изучение натуральных чисел на уроках математики в начальной школе представляет для младших школьников некоторые трудности. Для того, чтобы учащиеся освоили материал, необходимо развивать у них познавательную активность, этому могут способствовать уроки с использованием дидактических игр.

Следующая глава будет посвящена экспериментальному изучению дидактической игры как средства развития познавательной активности при изучении чисел первого десятка.

Глава 2. Реализация комплекса дидактических игр при изучении темы «Нумерация чисел первого десятка»

Похожие работы

Игра как средство развития познавательных процессов младших школьников

Скачать

183307

10

16

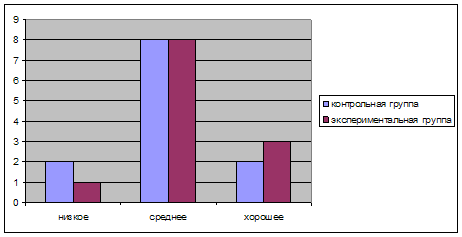
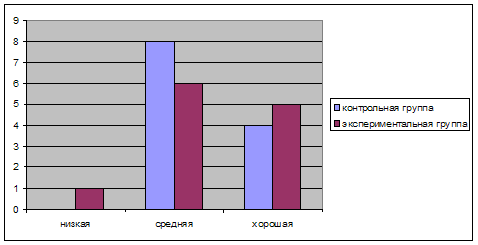
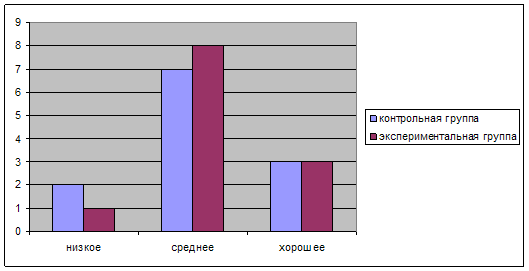
... что качественные изменения в экспериментальной группе выше, чем в контрольной. Результативность проведенной работы по развитию познавательных процессов младших школьников с использованием игр очевидна и представлена в линейных диаграммах 1 - 6. Таким образом, игра – эффективное средство развития познавательных способностей детей в младшем школьном возрасте.         Диаграмма 1. ...

Использование наглядных пособий в процессе изучения чисел первого десятка

Скачать

73355

2

1

... пособий в процессе изучения чисел первого десятка нами был проведен формирующий этап эксперимента, о котором пойдет речь в следующем параграфе. 2.2 Организация работы по использованию наглядных пособий в процессе изучения чисел первого десятка Одним из центральных понятий начального курса математики является понятие натурального числа. Оно трактуется как количественная характеристика класса ...

Игра, как средство развития творческого начала детей младшего школьного возраста

Скачать

114818

6

0

... , а также на уроках разного типа. Дидактическая игра входит в целостный педагогический процесс, сочетается и взаимосвязана с другими формами обучения и воспитания младших школьников.     2 Игра как средство развития творческого начала учащихся начальных классов 2.1 Дидактическая игра как средство активизации внимания и развития ...

Дидактические игры в начальном курсе математики

Скачать

131399

1

18

... 1991. 31.      Жикалкина Т.К. Игровые и занимательные задания по математике. М.: “Просвещение”, 1989. 32.      Истомина Н.Б. Активизация учащихся на уроках математики в начальных классах. М., 1985. 33.      Карпова Е.В. Дидактические игры в начальный период обучения. Ярославль: “Академия развития", 1997. 34.      Коваленко В.Г. Дидактические игры на уроках математики. М.: “Просвещение”, 1990. ...