Навигация
Модель старения Маккендрика фон Фёрстера
3. Модель старения Маккендрика фон Фёрстера
Для математического описания индивидуального развития Маккендрик и фон Фёрстер разработали рекуррентную модель, в которой непрерывный процесс старения рассматривается как последовательность отдельных, изолированных, актов. С математической точки зрения речь идет о том, чтобы вывести систему дифференциальных уравнений для функции плотности x, описывающей, сколько особей возраста г существуют в системе в момент времени t. Рассмотрим такую систему
в момент времени t + At. Число особей, которые к этому времени достигнут возраста г, равно числу особей, которые к моменту времени t достигли возраста г – At, за вычетом особей, умерших за интервал времени At. В результате мы получаем:
![]()
где D – смертность. Совершая предельный переход при At – О, приходим к дифференциальному уравнению
![]()
Важную роль в динамике системы играют также процессы воспроизводства, характеризуемые рождаемостью В. Эта величина показывает, сколько потомков производят в момент времени t особи, достигшие возраста т. В качестве начального условия по г для уравнения мы получаем величину
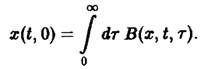
Оно дополняется заданием второго начального условия
![]()
Уравнения, с начальными условиями, задают модель Маккендрика–фон Фёрстера для популяций с возрастной структурой. Эта модель позволяет определить временную эволюцию функции плотности x по заданному начальному распределению у, если известны скорость воспроизведения и смертность. Решения, получаемые в рамках этой модели при различных конкретных функциях D и В, подробно изучены (McKendrick, 1926; von Foerster, 1959; Полу-эктов, 1974; Полуэктов и др., 1980; Романовский и др., 1984). Смертность D и рождаемость В, вообще говоря, сложным образом зависят от плотности x и), что приводит к существованию разнообразных структур решений. Однако уравнения в этом случае также становятся весьма сложными, и их аналитическое решение становится невозможным. Поэтому мы сначала рассмотрим простейший случай, когда рождаемость и смертность линейны по плотности x и не зависят явно от времени:
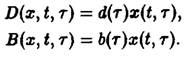
Реалистические примеры функций![]() и
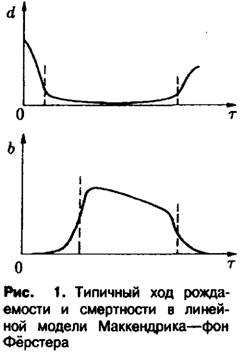
и![]() представлены на рис. 1. Смертность по прошествии первого времени после рождения стабилизируется на относительно низком уровне и начинает снова возрастать лишь при больших г; в дальнейшем мы, кроме того, принимаем предположение
представлены на рис. 1. Смертность по прошествии первого времени после рождения стабилизируется на относительно низком уровне и начинает снова возрастать лишь при больших г; в дальнейшем мы, кроме того, принимаем предположение
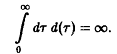
Рождаемость, как правило, достигает своего максимального значения лишь по истечении определенного периода после начала фазы зрелости и в старости снова понижается.
Учитывая соотношения, мы получаем из уравнений – систему уравнений
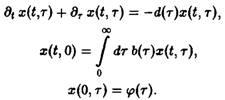
Поведение решений системы уравнений вполне очевидно. Из первого уравнения мы получаем, прежде всего, вероятность W того, что особь достигает возраста т:
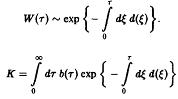
В зависимости от величины К возможны три качественно различных случая. При К > 1 число новорожденных в единицу времени больше числа умерших, доминируют процессы воспроизводства, и при t → оо мы получаем при всех г расходящуюся плотность x – оо. Наоборот, при К<1 воспроизводство слишком слабо, и при t – оо мы получаем x –* О при всех т, т.е. вид вымирает. Наконец, при К = I оба процесса находятся в равновесии, соответственно, существует бесконечно много стационарных состояний, и только от начального условия <р зависит, какое из них реализуется. Разумеется, в случаях К > 1 и К < 1 результат не зависит от начального условия <р.
Тем самым мы получаем качественную характеристику динамики индивидуального развития внутри отдельного вида при упрощающем предположении. Исследуем теперь, какие модификации возникают в том случае, когда п видов развиваются в соответствии с уравнениями, аналогичными уравнению, и, кроме того, взаимодействуют между собой посредством процесса отбора. Затронутая проблема связана с вопросом оптимальной стратегии старения, сложившимся в ходе эволюции.
4. Процессы отбора в моделях с непрерывным старением
Прежде всего систему п не взаимодействующих между собой видов можно описать уравнениями, обобщающими уравнение:
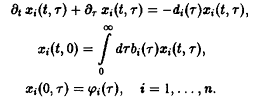
В качестве простого метода создания давления отбора мы по аналогии с моделью Эйгена потребуем постоянства общего числа особей в системе:

Чтобы условие выполнялось, необходимо модифицировать систему уравнений 13, что можно осуществить различными способами. Особый интерес представляют две возможности.
Похожие работы
... детей, развитии их интеллектуальной сферы. В формирующем эксперименте показана методика совершенствования реализации цели исследования, обозначены использованные средства работы по воспитанию экологической культуры у детей старшего дошкольного возраста и её содержание. II.3 Анализ и результаты исследования Чтобы убедиться в эффективности используемого формирующего эксперимента, был ...
... стоящая за ним проблема информатизации общества. Внедрение современных информационных технологий в библиотечную деятельность, возможность предоставления информации из сколь угодно удаленных источников по каналам связи коренным образом меняют положение библиотек в стуктуре современного общества. Принципиально по-новому решаются проблемы своевременного получения научной информации, без чего сегодня ...
... о формировании в сознании искаженной картины мира, складывающейся в результате ряда целенаправленных воздействий. Цель - рассмотреть и проанализировать особенности современного процесса глобализации как этапа социальной эволюции. Для достижения поставленной цели решаются следующие задачи: изучить глобализацию как социально-философскую проблему; исследовать социальный феномен глобализации как ...
... их поставщиком. То какая цена будет, на предлагаемые SPA-услуги индивидуальное решение каждого салона. Главное, чтобы услуга продавалась и приносила прибыль салону. 3. SPA как новый вид услуг в салоне красоты (на примере студии загара и красоты "Солана" 3.1 Анализ рынка салонов красоты Ростова-на-Дону, предоставляющих SPA-услуги Развитие российского рынка индустрии красоты и рынка услуг, ...


0 комментариев