Навигация
Введение потоковых членов в модель Эйгена
1. Введение потоковых членов в модель Эйгена.
Такая операция соответствует подстановкам

в уравнение, причем во избежание патологии, например, отрицательных концентраций, должны выполняться неравенства
![]()
2. Регуляция скорости воспроизведения.
Регуляция достигается с помощью подстановки
![]()
И в том, и в другом случае существенно, что модификации либо видо-, либо возрастоспециф ич ны.
Если равенство продифференцировать по времени и воспользоваться уравнением с подстановками, то получится следующее:
![]()
где по определению

Учитывая положительность
![]()
мы получаем

и, наконец, приходим к системе уравнений
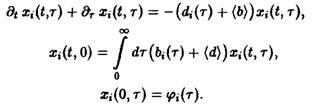
Проводя аналогичные вычисления с использованием подстановок, получаем, полагая
![]()
систему уравнений
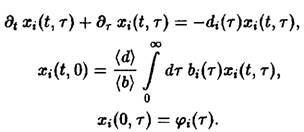
Уравнения и описывают временную эволюцию систем стареющих конкурирующих между собой видов и тем самым удобны для математического анализа индивидуального развития и отбора.
В отличие от системы уравнений для независимых видов дифференциальные уравнения и связаны между собой через определенное соотношением среднее значение. С одной стороны, эта связь выступает как математическое выражение взаимодействия между видами, а с другой – исключает возможность получения аналитических решений и обусловливает тем самым весьма широкое применение численных методов.
Ряд интересных утверждений может быть высказан и без явного решения системы уравнений. В частности, необходимо выяснить, каким образом, зная функции d, и Ь, можно определить те виды, которые замещают другие и поэтому доминируют при больших временах.
Необходимый для этого качественный анализ динамики удается осуществить с помощью подстановок
![]()
где
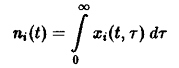
– общее число частиц,
![]()
– нормированная возрастная структура i-ro рода. Рассмотрим сначала ситуацию, описываемую уравнением. Пользуясь подстановкой, получаем следующие уравнения для п, и pi:
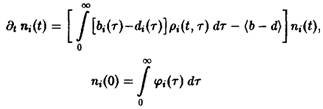
и

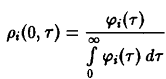
Уравнение имеет в точности такую же структуру, как уравнение Эйгена, с тем лишь различием, что теперь приспособленность
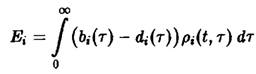
– функционал нормированной возрастной структуры![]() и поэтому может изменяться во времени.
и поэтому может изменяться во времени.
Его временная эволюция определяется изменением во времени возрастное структуры![]() , которая в свою очередь зависит от динамики чисел через уравнение. Зависимость приспособленности нормированной возрастной структуры приводит к тому, что виды могут повысить свои шансы на успех в ходе отбора за счет подходящего распределения особей по возрастным группам; иначе говоря, в ходе эволюции происходит замещение одних видов другими с оптимальной возрастное структурой. Каким образом по заданным функциям
, которая в свою очередь зависит от динамики чисел через уравнение. Зависимость приспособленности нормированной возрастной структуры приводит к тому, что виды могут повысить свои шансы на успех в ходе отбора за счет подходящего распределения особей по возрастным группам; иначе говоря, в ходе эволюции происходит замещение одних видов другими с оптимальной возрастное структурой. Каким образом по заданным функциям ![]() можно определить какие виды выживут в конце концов? Чтобы ответить на этот вопрос, рассмотри стационарные решения уравнений и при больших временах
можно определить какие виды выживут в конце концов? Чтобы ответить на этот вопрос, рассмотри стационарные решения уравнений и при больших временах
Мы получаем
![]()
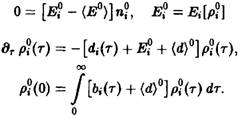
При рассмотрении уравнения Эйгена мы обнаружили, что уравнение допускает п различных стационарных решений вида
![]()
т.е. стационарны только такие ситуации, в которых все N особей представлены одним видом. С учетом соотношения из формулы следует, что

поэтому уравнение для ![]() замыкается. Таким образом, мы получаем:
замыкается. Таким образом, мы получаем:
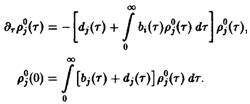
Вводя сокращенные обозначения
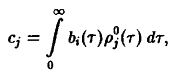
запишем уравнение в виде

и далее, с помощью соотношения,
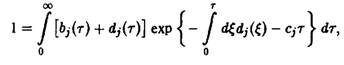
а также
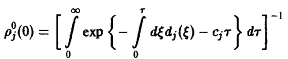
вследствие того, что по определению р,

Тем самым мы полностью охарактеризовали стационарные решения систем уравнений. Можно показать, что при заданных ![]() и
и ![]() уравнение всегда допускает ровно одно решение
уравнение всегда допускает ровно одно решение![]()
Величины Cj в силу соотношения определяют, поэтому![]() однозначно определяются соотношением.
однозначно определяются соотношением. ![]()
Из стационарных решений устойчиво только одно, и при t –* оо именно оно описывает поведение системы. Для этого решения справедливы неравенства
![]()
т.е. выживает вид, обладающий наибольшей приспособленностью. Соотношения – позволяют определить этот вид посредством формулы
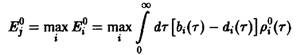
по известным функциям ![]() . Тем самым для системы конкурирующих видов с возрастной структурой, описываемой уравнением, становится возможным определять на основе заданных зависящих от возраста скорости воспроизведения и смертности тот из видов, который побеждает в ходе отбора. Используя соотношения, получаем
. Тем самым для системы конкурирующих видов с возрастной структурой, описываемой уравнением, становится возможным определять на основе заданных зависящих от возраста скорости воспроизведения и смертности тот из видов, который побеждает в ходе отбора. Используя соотношения, получаем
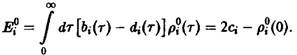
Можно показать, что
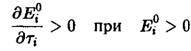
Таким образом, если мы ограничимся видами с![]() т.е. такими, которые в отсутствие отбора сами не вымирают и то максимум величины
т.е. такими, которые в отсутствие отбора сами не вымирают и то максимум величины ![]() достигается для того вида j, для которого величина
достигается для того вида j, для которого величина![]() также максимальна. Следовательно, доминирующий вид может определяться вместо соотношения соотношением
также максимальна. Следовательно, доминирующий вид может определяться вместо соотношения соотношением
![]()
где с, – определяется формулой. Аналогичные соображения применимы и к модели (Эбелинг и др., 1986). Следует отметить, что в рассматриваемом случае соотношение получается и как определяющее уравнение для выживающего вида. Если воспользоваться определением параметров с, то соотношение можно рассматривать как разумное обобщение соотношения.
В заключение продемонстрируем важность внутривидовой возрастной структуры для процесса отбора на простом примере динамики, описываемой уравнением. Рассмотрим два вида с одинаковой и постоянной смертностью
![]()
и рождаемостью

где в и в последующих соотношениях верхние знаки относятся к первому виду, а нижние – ко второму виду. Выбранные рождаемости представлены на рис. 2. Чтобы выяснить, какой вид побеждает в процессе отбора, необходимо исследовать, какая из определяемых соотношением величин с, больше. В рассматриваемом случае равенство упрощается до

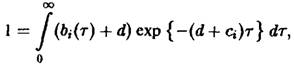
или
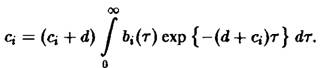
Отсюда с учетом формулы получаем
![]()
![]()
Подставляя ![]() находим
находим
![]()
Графическое решение этого уравнения представлено на рис. 3. Из хода кривой мы заключаем, что Х < х2 вследствие монотонности подстановки приводит к неравенству с > С2 – Таким образом, первый вид выживает, а второй вымирает; грубо говоря, те преимущества, которыми второй вид обладает в старости, не перевешивают его недостатков в юности. Этот пример наглядно демонстрирует упрощенное описание процесса отбора с учетом возрастной структуры. В случае динамики Эй-гена оба вида характеризовались бы усредненной приспособленностью, в результате чего никакого отбора не происходило бы, и оба вида могли бы сосуществовать.
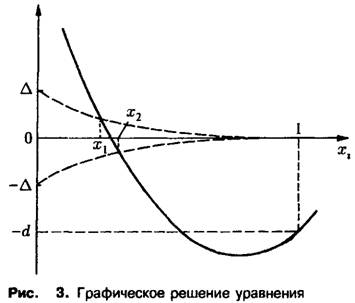
![]()
Действительно, при одинаковых начальных условиях
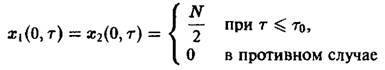
мы получаем из соотношения
![]()
Однако динамика внутривидовой возрастной структуры![]() приводит к временному изменению приспособленности:
приводит к временному изменению приспособленности:
![]()
Тем самым даже в простейших моделях индивидуальное развитие внутри видов имеет решающее значение для исхода протекающих процессов отбора. Другие простые примеры для функций ![]() показывают, что обычно высокая скорость воспроизведения и низкая смертность в сравнительно молодом возрасте является преимуществом в борьбе за отбор. Это обстоятельство тесно связано с тем, что стационарные возрастные структуры
показывают, что обычно высокая скорость воспроизведения и низкая смертность в сравнительно молодом возрасте является преимуществом в борьбе за отбор. Это обстоятельство тесно связано с тем, что стационарные возрастные структуры![]() монотонно затухают по
монотонно затухают по![]() .
.
5. Сложные возрастные структуры
Можно указать несколько случаев, когда более сложные и, следовательно, более реалистические возрастные структуры удается описать с помощью модели Маккендрика фон Фёрстера и ее обобщения. Мы не будем предпринимать попыток решить соответствующие уравнения, а ограничимся изложением возможностей, присущих формализму.
Прежде всего, напомним наиболее общую форму – модели в случае одного отдельного вида:
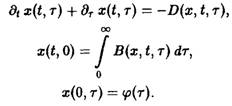
Множество самых различных решений определяется выбором функций D (x, t, т) и В. В дальнейшем мы обсудим лишь несколько принципиальных вариантов. Соображения, развиваемые ниже относительно функции D, могут быть по аналогии перенесены на рождаемость В.
Прежде всего, мы предположим существование явной зависимости от времени. Это позволит учитывать изменения внешних условий. Колебания могли бы моделировать годичные или более длительные изменения, чередования теплых и холодных периодов, а скачкообразные изменения – влияние природных катаклизмов на экосистемы. Существуют и другие разнообразные условия, приводящие как к положительным, так и к отрицательным последствиям, но их вряд ли уместно классифицировать более подробно.
В дальнейшем мы всегда будем предполагать, что система всегда находится в стационарном окружающем поле. Явная зависимость от времени в этом случае не возникает, но изменение величины D в зависимости от плотности х может быть весьма разнообразным. Рассмотрим сначала простейший случай – зависимость от х,
![]()
Несколько более реалистическим является учет ограничивающего члена в виде
![]()
препятствующем для К > 1) расходимости ![]() при
при ![]() Если число особей очень велико, то смертность сильно возрастает и система стабилизируется на уровне, зависящем от функций
Если число особей очень велико, то смертность сильно возрастает и система стабилизируется на уровне, зависящем от функций ![]() i. В
i. В ![]() могут быть включены члены более высокого) порядка. Включение кубической нелинейности может привести к возникновению бистабильных ситуаций, в которых число особей
могут быть включены члены более высокого) порядка. Включение кубической нелинейности может привести к возникновению бистабильных ситуаций, в которых число особей ![]() может устанавливаться на двух, вообще говоря, не зависящих от г устойчивых значениях.
может устанавливаться на двух, вообще говоря, не зависящих от г устойчивых значениях.
Однако возможные режимы этим отнюдь не исчерпываются. Особенно большой интерес наряду с перечисленными выше вариантами нелокальных зависимостей представляют такие, которые в простейшей форме могут быть записаны следующим образом:
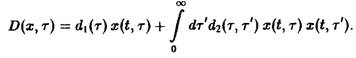
Ядро интеграла ![]() описывает взаимодействие между особями самых различных возрастов внутри одного вида. При
описывает взаимодействие между особями самых различных возрастов внутри одного вида. При ![]() эффективная смертность особей, достигших возраста г, понижается за счет наличия особей возраста
эффективная смертность особей, достигших возраста г, понижается за счет наличия особей возраста ![]() . Примером может служить, например, особенно тщательная забота о потомстве на протяжении первых отрезков жизни или поддержка старых, весьма опытных особей. Соответственно,
. Примером может служить, например, особенно тщательная забота о потомстве на протяжении первых отрезков жизни или поддержка старых, весьма опытных особей. Соответственно, ![]() приводит к внутривидовой конкуренции, проявляющейся в борьбе за верховенство или в "конфликтах поколений". Как и в соотношение, в формулу могут входить члены высшего порядка, описывающие взаимодействие между тремя и более различными возрастными группами.
приводит к внутривидовой конкуренции, проявляющейся в борьбе за верховенство или в "конфликтах поколений". Как и в соотношение, в формулу могут входить члены высшего порядка, описывающие взаимодействие между тремя и более различными возрастными группами.
Введение давления отбора с помощью условия постоянства организации в целом позволяет моделировать только простейшую форму межвидовой конкуренции. Взаимодействие хищник-жертва можно рассматривать как обобщение взаимодействия вида.
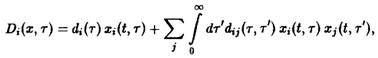
Похожие работы
... детей, развитии их интеллектуальной сферы. В формирующем эксперименте показана методика совершенствования реализации цели исследования, обозначены использованные средства работы по воспитанию экологической культуры у детей старшего дошкольного возраста и её содержание. II.3 Анализ и результаты исследования Чтобы убедиться в эффективности используемого формирующего эксперимента, был ...
... стоящая за ним проблема информатизации общества. Внедрение современных информационных технологий в библиотечную деятельность, возможность предоставления информации из сколь угодно удаленных источников по каналам связи коренным образом меняют положение библиотек в стуктуре современного общества. Принципиально по-новому решаются проблемы своевременного получения научной информации, без чего сегодня ...
... о формировании в сознании искаженной картины мира, складывающейся в результате ряда целенаправленных воздействий. Цель - рассмотреть и проанализировать особенности современного процесса глобализации как этапа социальной эволюции. Для достижения поставленной цели решаются следующие задачи: изучить глобализацию как социально-философскую проблему; исследовать социальный феномен глобализации как ...
... их поставщиком. То какая цена будет, на предлагаемые SPA-услуги индивидуальное решение каждого салона. Главное, чтобы услуга продавалась и приносила прибыль салону. 3. SPA как новый вид услуг в салоне красоты (на примере студии загара и красоты "Солана" 3.1 Анализ рынка салонов красоты Ростова-на-Дону, предоставляющих SPA-услуги Развитие российского рынка индустрии красоты и рынка услуг, ...


0 комментариев