Навигация
При заданій сукупності вузлових точок будова багаточлена можлива тільки єдиним способом
1. При заданій сукупності вузлових точок будова багаточлена можлива тільки єдиним способом.
2. Багаточлен Лагранжа може бути побудовано при будь-якому розташуванні вузлів інтерполяції (включаючи і нерівномірне).
У розгорнутому виді форма Лагранжа має вид:
Рn(х)= 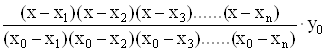 +
+
+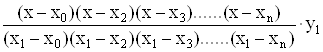 +
+
+ … + 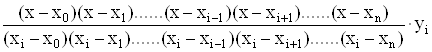 +
+
+ … +  .(6)
.(6)
При n=1 формула Лагранжа має вид:
Р(х) =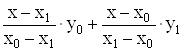 (7)
(7)
і називається формулою лінійної інтерполяції.
При n=2 одержимо формулу квадратичної інтерполяції:
Р(х)=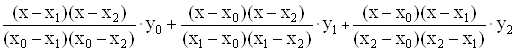 . (8)
. (8)
4. ЗВОРОТНА ІНТЕРПОЛЯЦІЯ
Нехай функція у= f(х) задана таблицею. Задача зворотної інтерполяції полягає в тому, щоб по заданому значенню функції у визначити відповідне значення аргументу х.
Якщо вузли інтерполяції x0, x1, x2, … xn нерівновіддалені, задача легко вирішується за допомогою інтерполяційної формули Лагранжа (5). Для цього достатньо прийняти у за незалежну змінну, а х вважати функцією. Тоді отримаємо
x = 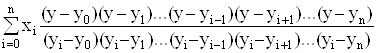 (9)
(9)
Розглянемо тепер задачу зворотної інтерполяції для випадку рівновіддалених вузлів інтерполяції. Припустимо, що функція f(х) монотонна і дане значення у знаходиться між y0=f(x0) і y1 = f(x1).
Замінюючи функцію у=f(x) першим інтерполяційним багаточленом Ньютона, одержимо:
y = y0 + q Dy0 + ![]() D2y0 +
D2y0 + ![]() D3y0 +…+
D3y0 +…+ ![]() Dny0 .
Dny0 .
Звідси
q = 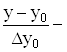 D2y0
D2y0 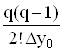 – …–Dny0
– …–Dny0 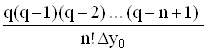 ,
,
тобто q=j(q).
Розмір q визначаємо методом послідовних наближень як границю послідовності:
q = ![]() ,
,
де qi = j (qi–1) (i=1, 2,…).
За початкове наближення приймаємо
q0 = 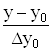 (10)
(10)
Для i-го наближення маємо:
qi = q0 – D2y0  – …–Dny0
– …–Dny0 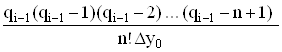 . (11)
. (11)
На практиці ітераційний процес продовжують доти, поки не установляться значення, що відповідають необхідній точності, причому q » qm, де m – останнє зі знайдених наближень. Знайдемо q, визначаємо х по формулі
![]() = q,
= q,
звідки
х = x0 + q h.(12)
Ми застосували метод ітерації для рішення задачі зворотної інтерполяції, користуючись першою інтерполяційною формулою Ньютона. Аналогічно можна застосувати цей спосіб і до другої формули Ньютона:
y = yn + qDyn–1 + ![]() D2yn–2 +
D2yn–2 + ![]() D3 yn–3 + …
D3 yn–3 + …
+ ![]() Dny0 .
Dny0 .
Звідси
q = 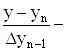 D2yn-2
D2yn-2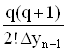 – …–Dny0
– …–Dny0 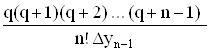 ...
...
Позначимо q0 = 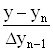 – початкове наближення.
– початкове наближення.
Для i-го наближення маємо:
qi = q0–D2yn–2 – …–Dny0
– …–Dny0 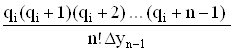 ... (13)
... (13)
Знайдемо
q = ![]() ,
,
визначимо х по формулі
х = xn + q h .[3], [2]
Далі розглянемо запропоновану мені інтерполяційну формулу Бесселя, яка часто використовується для знаходження значення функції у між вузловій точці. Вона подібна до інтерполяційної формули Стерлінга і обидві вони є похідними від першої та другої інтерполяційних формул Гауса.
ІНТЕРПОЛЯЦІЙНА ФОРМУЛА БЕССЕЛЯ
Часто використовується інтерполяційна формула Бесселя. Для виведення цієї формули скористаємось другою інтерполяційною формулою Гауса:
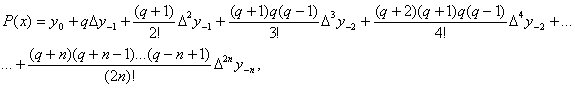
у скороченому вигляді:
![]()
де х=х0+qh
Візьмемо 2n+2 рівновіддалених вузлів інтерполювання
x-n, x-(n-1),..., x0,..., xn-1, xn, xn+1
з кроком h, і нехай
yi= f(xi) (i =-n,…,n+1)
- задані значення функції y= f(x). ![]()
Якщо вибрати за початкові значення x= x0таy= y0, то, використовуючи вузли xk (k= 0, ±1, …,![]() n), будемо мати:
n), будемо мати:
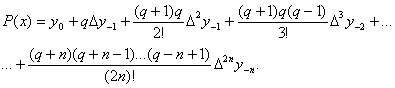 (1)
(1)
Приймемо тепер за початкові значення х=х1 і у=у1 і використаємо вузли х1+к(к=0, ![]() 1,...,
1,...,![]() n). Тоді
n). Тоді
![]()
причому відповідно індекси всіх різниць в правій частині формули (1) зростуть на одиницю. Замінивши в правій частині формули (1) q на q-1 і збільшивши індекси всіх різниць на 1 , отримаємо допоміжну інтерполяційну формулу
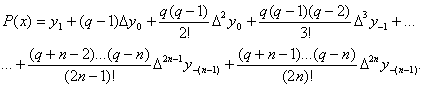 (2)
(2)
Взявши середнє арифметичне формул (1) і (2), після простих перетворень отримаємо інтерполяційну формулу Бесселя
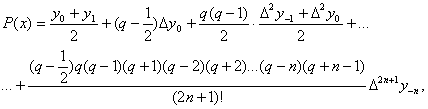 (3)
(3)
де ![]()
Інтерполяційна формула Бесселя (3), як слідує з способа отримання її, представляє собою поліном, що співпадає з даною функцією y= f(x) в 2n+2 точках
x-n , x-(n-1),…, xn , xn+1.
В частинному випадку, при n=1, нехтуючи різницею ∆3y-1, отримаємо формулу квадратичної інтерполяції по Бесселю
P(x)=![]()
Або
![]()
де
![]()
В формулі Бесселя всі члени, які містять різниці непарного порядку, мають множник q-![]() ; тому при
; тому при ![]() формула (3) значно спрощується :
формула (3) значно спрощується :
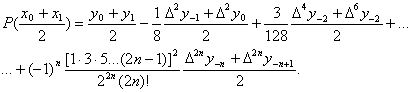
Цей спеціальний випадок формули Бесселя називається формулою інтерполювання на середину. Якщо в формулі Бесселя (3) зробити заміну по формулі ![]()
то вона приймає більш симетричний вид

де ![]()
ЗАГАЛЬНИЙ ОПИС ПРОГРАМИ
В програмі використано кілька процедур та функцій, в яких використовуються різноманітні позначення, змінні та тому подібне. Тому далі буде дано пояснення (розшифровування) що яким символом, чи їх сукупністю позначено.
PROCEDURE vvod – процедура введення даних, тобто задання початкових умов (кількість вузлів, задаються X та відповідні їм Y, а також X, в яких потрібно знайти значення ф-ї).
PROCEDURE ddd –дана процедура формує трикутну таблицю різниць значень
ф-ї.
PROCEDURE rech- процедура рішення задачі за інтерполяційною формулою Бесселя.
PROCEDURE vivod- це процедура виведення результатів роботи програми, які виводяться файлі f2, який має назву «ANA.NAS».
FUNCTION pos1 (j, q: real): real; - функція, яка обчислює для формули Бесселя чисельник її доданків.
FUNCTION fak (j: integer): real; - функція для обрахунку факторіала в знаменнику доданків формули.
Також в програмі використовуються такі позначення:
kol- позначено кількість точок (вузлів), в яких потрібно знайти значення функції.
zad- назва масива, в який заносимо ікси, значення функції в яких бажаємо знайти.
otv- назва масива для відповідних ігреків.
f1- це файл, який має назву «st1.tab», з нього читаються задані ікси та ігреки.
f2- файл, який має назву «ana.nas», - це файл виведення, з нього читаються результати роботи програми.
n- кількість вузлів інтерполяції.
h- крок задання точок.
Література
1. Вычислительная техника в инженерных и экономических расчетах
/ А.В.Крушевский, А.В.Беликов, В.Д.Тищенко – Киев: «Высшая школа». Главное изд-во, 1985. – 290 с.
2. Дифференциальное и интегральное исчисления /Н.С.Пискунов- Москва: «Наука». Главная редакция физико-математической литературы, 1978.-576 с.
3.Численые методы в инженерных исследованиях /В.Е.Краскевич, К.Х.Зеленский, В.И.Гречко - Киев: Главное изд-во «Высшая школа», 1986.-263 с.
Похожие работы
... ефективності, що враховує затрати часу та пам'яті для його виконання, за даним методом. Третій розділ містить інструкція користувача, лістинг та опис програми і результати тестування. 1. Аналіз теоретичної бази інтерполювання функції 1.1 Постановка задачі інтерполяції Якщо задано певну довільну функцію на деякому проміжку , то обчислити її значення непросто. Для полегшення цієї задачі є ...
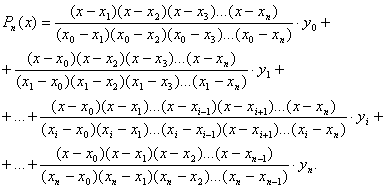
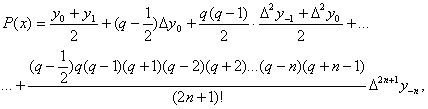

0 комментариев