СОРТИРОВКА С ПОМОЩЬЮ СРАВНЕНИЙ

3.3. СОРТИРОВКА С ПОМОЩЬЮ СРАВНЕНИЙ

Здесь мы изучим задачу упорядочения последовательности из п элементов, взятых из линейно упорядоченного множества 5, о структуре которых ничего не известно. Информацию об этой после­довательности можно получить только с помощью операции сравне­ния двух элементов. Сначала мы покажем, что любой алгоритм, упорядочивающий с помощью сравнений, должен делать по крайней мере О (n log n) сравнений на некоторой последовательности дли­ны n. Пусть надо упорядочить последовательность, состоящую из n различных элементов а_г, а₂, . . . , а_n.

Алгоритм, упорядочивающий с помощью сравнений, можно представить в виде дерева решений так, как описано в разделе 1.5. На рис. 1.18 изображено дерево реше­ний, упорядочивающее последовательность a, b, c. Далее мы пред­полагаем, что если элемент a сравнивается с элементом b в некотором узле v дерева решений, то надо перейти к левому сыну узла v при a < b и к правому — при a  b.

Как правило, алгоритмы сортировки, в которых для разветвле­ния используются сравнения, ограничиваются сравнением за один раз двух входных элементов. В самом деле, алгоритм, который ра­ботает на произвольном линейно упорядоченном множестве, не мо­жет никак преобразовать входные данные, поскольку при самой об­щей постановке задачи операции над данными "не имеют смысла". Так или иначе, мы докажем сильный результат о высоте любого де­рева решений, упорядочивающего последовательность из п эле­ментов.

Лемма 3.1. Двоичное дерево высоты Н содержит не более 1^п ли­стьев.

Доказательство. Элементарная индукция по h. Нужно лишь заметить, что двоичное дерево высоты h составлено из корня и самое большее двух поддеревьев, каждое высоты не более h - 1 .

Теорема 3.4. Высота любого дерева решений, упорядочивающего последовательность из п различных элементов, не меньше log n!.

Доказательство. Так как результатом упорядочения последовательности из п! элементов может быть любая из п\ переста­новок входа, то в дереве решений должно быть по крайней мере n! листьев. По лемме 3.1 высота такого дерева должна быть не меньше log n!.

Следствие. В любом алгоритме, упорядочивающем с помощью сравнений, на упорядочение последовательности из п элементов тра­тится не меньше сп log п сравнений при некотором с>0 и достаточ­но большом п.

Доказательство. Заметим, что при n >1

n!n(n-1)(n-2)…()() ,

так что log n!(n/2)log(n/2)(n/4)log n при n 4

По формуле Стирлинга точнее приближает n!функция (п/е)^п, так что n(log п — log е)=п log п — 1,44n служит хорошим приближе­нием нижней границы числа сравнений, необходимых для упорядо­чения последовательности из п элементов.

3.4. СОРТ ДЕРЕВОМ — УПОРЯДОЧЕНИЕ С ПОМОЩЬЮ О(n log n) СРАВНЕНИЙ

Так как любой сортирующий алгоритм, упорядочивающий с помощью сравнений, затрачивает по необходимости п log п срав­нений для упорядочения хотя бы одной последовательности длины n, естественно спросить, существуют ли сортирующие алгоритмы, затрачивающие не более О (п log п) сравнений для упорядочения любой последовательности длины п. Один такой алгоритм мы уже видели — это сортировка слиянием из разд. 2.7. Другой алгоритм — Сортдеревом. Помимо того, что это полезный алгоритм упорядо­чения, в нем используется интересная структура данных, которая находит и другие приложения.

Сортдеревом лучше всего понять в терминах двоичного дерева вроде изображенного на рис. 3.5, у которого каждый лист имеет глубину d. или d-1. Узлы дерева помечаются элементами последова­тельности, которую хотят упорядочить. Затем Сортдеревом меняет размещение этих элементов на дереве до тех пор, пока элемент, соответствующий произвольному узлу, станет не меньше элементов, соответствующих его сыновьям. Такое помеченное дерево мы будем называть сортирующим.

Пример 3.3. На рис. 3.5 изображено сортирующее дерево. За­метим, что последовательность элементов, лежащих на пути из любого листа в корень, линейно упорядочена и наибольший эле­мент в поддереве всегда соответствует его корню.

На следующем шаге алгоритма Сортдеревом из сортирующего дерева удаляется наибольший элемент — он соответствует корню дерева. Метка некоторого листа переносится в корень, а сам лист уда­ляется. Затем полученное дерево переделывается в сортирующее, и процесс повторяется. Последовательность элементов, удаленных из сортирующего дерева, упорядочена по невозрастанию.

Удобной структурой данных для сортирующего дерева служит такой массив А, что А[1] — элемент в корне, а А[2i] и A[2i+1] – элементы в левом и правом сыновьях (если они существуют) того узла, в котором хранится А[i].

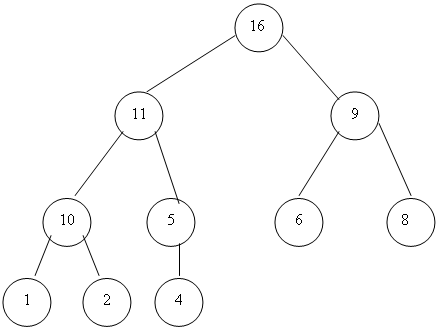
Рисунок 3.5 Сортирующее дерево.

Например, сортирующее дерево на рис. 3.5 можно представить массивом

4

11

9

10

5

6

8

1

2

16

Заметим, что узлы наименьшей глубины стоят в этом массиве первыми, а узлы равной глубины стоят в порядке слева направо.

Не каждое сортирующее дерево можно представить таким спо­собом. На языке представления деревьев можно сказать, что для образования такого массива требуется, чтобы листья самого низ­кого уровня стояли как можно левее (как, например, на рис. 3.5).

Если сортирующее дерево представляется описанным массивом, то некоторые операции из алгоритма Сортдеревом легко выполнить. Например, согласно алгоритму, нужно удалить элемент из корня, где-то запомнить его, переделать оставшееся дерево в сортирующее и удалить непомеченный лист. Можно удалить наибольший эле­мент из сортирующего дерева и запомнить его, поменяв местами A[1] и A[n], и затем не считать более ячейку п нашего массива частью сортирующего дерева. Ячейка п рассматривается как лист, удаленный из этого дерева. Для того чтобы переделать дерево, хра­нящееся в ячейках 1,2, ... , n—1, в сортирующее, надо взять новый элемент A[1] и провести его вдоль подходящего пути в дереве. Затем можно повторить процесс, меняя местами A[1] и A[п—1] и считая, что дерево занимает ячейки 1,2 … п—2 и т. д.

Пример 3.4. Рассмотрим на примере сортирующего дерева рис. 3.5, что происходит, когда мы поменяем местами первый и по­следний элементы массива, представляющего это дерево. Новый массив

16

11

9

10

5

6

8

1

2

4

соответствует помеченному дереву на рис. 3.6,а. Элемент 16 ис­ключается из дальнейшего рассмотрения. Чтобы превратить полу­ченное дерево в сортирующее, надо поменять местами элемент 4 с большим из его сыновей, т. е. с элементом 11.

В своем новом положении элемент 4 обладает сыновьями 10 и 5. Так как они больше 4, то 4 переставляется с 10, большим сыном. После этого сыновьями элемента 4 в новом положении становятся 1 и 2. Поскольку 4 превосходит их обоих, дальнейшие перестановки не нужны.

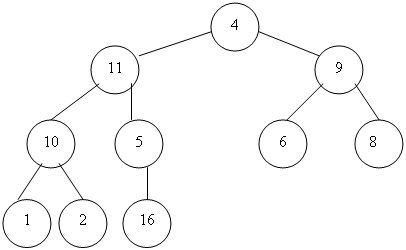
Рисунок 3.6. а — результат перестановки элементов 4 и 16 в сортирующем дерев

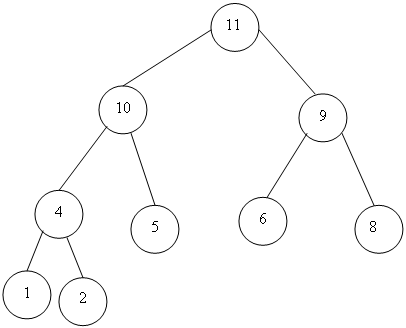
Рисунок 3.6; б — результат перестройки сортирующего дерева и удаления элемента 16.

Полученное в результате сортирующее дерево показано на рис. 3.6,6. Заметим, что хотя элемент 16 был удален из сортирующе­го дерева, он все же присутствует в конце массива А .

Теперь перейдем к формальному описанию алгоритма Сорт-деревом.

Пусть а_г, а₂, . . ., а_п — последовательность сортируемых эле­ментов. Предположим, что вначале они помещаются в массив А именно в этом порядке, т. е. A[i] = a,1in. Первый шаг состоит в построении сортирующего дерева, т. е. элементы в А перераспре­деляются так, чтобы удовлетворялось свойство сортирующего де­рева: A[i]A[2i] при 1 i n/2 и A[i]A[2i+1] при 1in/2. Это делают, строя, начиная с листьев, все большие и большие сор­тирующие деревья. Всякое поддерево, состоящее из листа, уже яв­ляется сортирующим. Чтобы сделать поддерево высоты h сортирую­щим, надо переставить элемент в корне с наибольшим из элементов, соответствующих его сыновьям, если, конечно, он меньше какого-то из них. Такое действие может испортить сортирующее дерево высоты h — 1, и тогда его надо снова перестроить в сортирующее. Приведем точное описание этого алгоритма.

Алгоритм 3.3. Построение сортирующего дерева

Вход. Массив элементов A[i], 1i n

Выход. Элементы массива А, организованные в виде сортирую­щего дерева, т. е.A[i]A[] для 1<in.

Метод. В основе алгоритма лежит рекурсивная процедура пересыпка. Ее параметры i и j задают область ячеек массива А, обладающую свойством сортирующего дерева; корень строящегося дерева помещается в i.

procedure ПЕРЕСЫПКА ((i,j):

1. if i — не лист и какой-то его сын содержит элемент, пре­восходящий элемент в i then begin

2. пусть k— тот сын узла i, в котором хранится

наибольший элемент;

3.                 переставить А[i] и А[k];

4.                 ПЕРЕСЫПКА (k,j)

5.                 end

Параметр j используется, чтобы определить, является ли i листом и имеет он одного или двух сыновей. Если i > j/2, то i — лист, и процедуре ПЕРЕСЫПКА(i,j) ничего не нужно делать, поскольку А[i] — уже сортирующее дерево.

Алгоритм, превращающий весь массив А в сортирующее дерево, выглядит просто:

procedure ПОСТРСОРТДЕРЕВА:

for i п¹) stер —1 until 1 do ПЕРЕСЫПКА (i,n)

Покажем, что алгоритм 3.3 преобразует А в сортирующее дере­во за линейное время.

Лемма 3.2. Если узлы i+1, i+2, . . ., n являются корнями сор­тирующих деревьев, то после вызова процедуры ПЕРЕСЫПКА (i, п) все узлы i, i+1, . . ., п будут корнями сортирующих деревьев.

Доказательство. Доказательство проводится возврат­ной индукцией по I.

Базис, т. е. случай i=п, тривиален, так как узел п должен быть листом и условие, проверяемое в строке 1, гарантирует, что ПЕ­РЕСЫПКА (п, п) ничего не делает.

Для шага индукции заметим, что если i — лист или у него нет сына с большим элементом, то доказывать нечего (как и при обо­сновании базиса). Но если у узла i есть один сын (т. е. если 2i=n) и A[i]<A[2i], то строка 3 процедуры ПЕРЕСЫПКА переставляет А[i] и А[2i]. В строке 4 вызывается ПЕРЕСЫПКА (2i, n); поэто­му из предположения индукции вытекает, что дерево с корнем 2i будет переделано в сортирующее. Что касается узлов i+1, i+2, . . . . . ., 2i — 1, то они и не переставали быть корнями сортирующих деревьев. Так как после этой новой перестановки в массиве А вы­полняется неравенство A[i]>A[2i], то дерево с корнем i также оказывается сортирующим.

Аналогично, если узел i имеет двух сыновей (т. е. если 2i+1n) и наибольший из элементов в А [2i] и в А [2i+1] больше элемента в A [i], то, рассуждая, как и выше, можно показать, что после вызова процедуры ПЕРЕСЫПКА(i,n) все узлы i, i+1,..., n будут кор­нями сортирующих деревьев.

Теорема 3.5. Алгоритм 3.3 преобразует А в сортирующее дере­во за линейное время.

Доказательство. Применяя лемму 3.2, можно с по­мощью простой возвратной индукции по i показать, что узел i становится корнем какого-нибудь сортирующего дерева для всех i, 1in

Пусть Т (h) — время выполнения процедуры ПЕРЕСЫПКА на узле высоты h. Тогда Т (h)Т (h — 1)+с для некоторой постоянной с. Отсюда вытекает, что Т (h) есть О (h).

Алгоритм 3.3 вызывает процедуру ПЕРЕСЫПКА, если не счи­тать рекурсивных вызовов, один раз для каждого узла. Поэтому время, затрачиваемое на ПОСТРСОРТДЕРЕВА, имеет тот же поря­док, что и сумма высот всех узлов. Но узлов высоты i не больше, чем . Следовательно, общее время, затрачиваемое процедурой ПОСТРСОРТДЕРЕВА, имеет порядок in/2, т.е O(n)

Теперь можно завершить детальное описание алгоритма СОРТДЕРЕВОМ. Коль скоро элементы массива А преобразованы в сор­тирующее дерево, некоторые элементы удаляются из корня по од­ному за раз. Это делается перестановкой А[1] и А[n] и последую­щим преобразованием A[1], А[2], ..., А[n - 1] в сортирующее дерево. Затем переставляются А[1] и А[n - 1], а A[1], А[2], ..., А [п - 2] преобразуется в сортирующее дерево. Процесс продол­жается до тех пор, пока в сортирующем дереве не останется один элемент. Тогда А[1], А[2], ..., А[n] — упорядоченная последова­тельность.

Алгоритм 3.4. Сортдеревом

Вход. Массив элементов А[i], 1in.

Выход. Элементы массива А, расположенные в порядке неубы­вания.

Метод. Применяется процедура ПОСТРСОРТДЕРЕВА, т. е. алгоритм 3.3. Наш алгоритм выглядит так:

begin

ПОСТРСОРТДЕРЕВА;

For in step -1 until 2 do

Begin

переставить А[1] и А[i];

ПЕРЕСЫПКА(i,i - 1)

End end

Теорема 3.6. Алгоритм 3.4 упорядочивает последовательность из п элементов за время 0(n log п).

Доказательство. Корректность алгоритма доказывает­ся индукцией по числу выполнений основного цикла, которое обозначим через m. Предположение индукции состоит в том, что по­сле m итераций список A[n-m+1], ..., А [n] содержит m наи­больших элементов, расположенных в порядке неубывания, а спи­сок A[1], ..., А[n-m] образует сортирующее дерево. Детали до­казательства оставляем в качестве упражнения. Время выполнения процедуры ПЕРЕСЫПКА(1, i) есть 0(log i)- Следовательно, ал­горитм 3.4 имеет сложность О (n log i ).

Следствие. Алгоритм Сортдеревом имеет временную сложность O(nlog n)