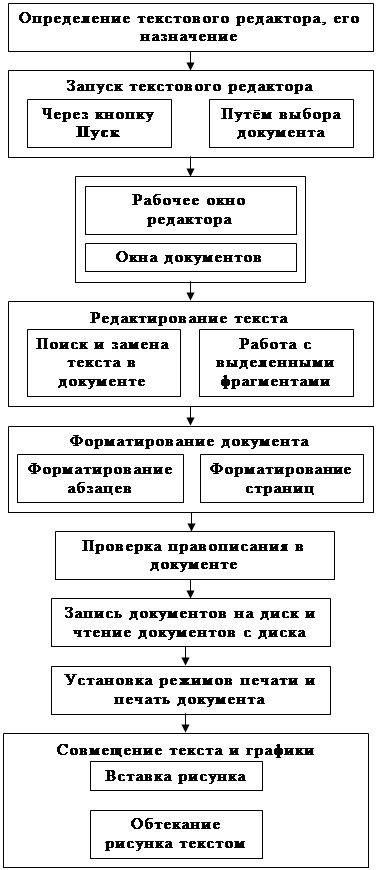
Навигация
БЫСТРСОРТ — УПОРЯДОЧЕНИЕ ЗА СРЕДНЕЕ ВРЕМЯ О(n log n)
3.5. БЫСТРСОРТ — УПОРЯДОЧЕНИЕ ЗА СРЕДНЕЕ ВРЕМЯ О(n log n)
До сих пор мы рассматривали поведение сортирующих алгоритмов только в худшем случае. Для многих приложений более реалистичной мерой временной сложности является усредненное время работы. В случае сортировки с помощью деревьев решений мы видим, что никакой сортирующий алгоритм не может иметь среднюю временную сложность, существенно меньшую n 1оg n. Однако известны алгоритмы сортировки, которые работают в худшем случае сn2 времени, где с — некоторая постоянная, но среднее время работы, которых относит их к лучшим алгоритмам сортировки. Примером такого алгоритма служит алгоритм Быстрсорт, рассматриваемый в этом разделе.
Чтобы можно было рассуждать о среднем времени работы алгоритма, мы должны договориться о вероятностном распределении входов. Для сортировки естественно допустить, что мы и сделаем, что любая перестановка упорядочиваемой последовательности равновероятна в качестве входа. При таком допущении уже можно оценить снизу среднее число сравнений, необходимых для упорядочения последовательности из n элементов.
Общий метод состоит в том, чтобы поставить в соответствие каждому листу v дерева решений вероятность быть достигнутым при данном входе. Зная распределение вероятностей на входах, можно найти вероятности, поставленные в соответствие листьям. Таким образом, можно определить среднее число сравнений, производимых данным алгоритмом сортировки, если вычислить сумму взятую по всем листьям дерева решений данного алгоритма, в которой рi — вероятность достижения i-го листа, а d![]() , - его глубина. Это число называется средней глубиной дерева решений. Итак, мы пришли к следующему обобщению теоремы 3.4.
, - его глубина. Это число называется средней глубиной дерева решений. Итак, мы пришли к следующему обобщению теоремы 3.4.
Теорема 3.7. В предположении, что все перестановки п-элементной последовательности появляются на входе с равными вероятностями, любое дерево решений, упорядочивающее последовательность из п элементов, имеет среднюю глубину не менее log n!.
Доказательство. Обозначим через D (Т) сумму глубин листьев двоичного дерева Т. Пусть D (Т) — ее наименьшее значение, взятое по всем двоичным деревьям Т с m листьями. Покажем индукцией по m, что D(m)![]() m log m.
m log m.
Базис, т. е. случай /п=1, тривиален. Допустим, что предположение индукции верно для всех значений m, меньших k. Рассмотрим дерево решений Т с и листьями. Оно состоит из корня с левым поддеревом Т с k листьями и правым поддеревом T![]() с k – 1 листьями при некотором i, 1
с k – 1 листьями при некотором i, 1![]() i
i![]() k. Ясно, что
k. Ясно, что
D(T)=i+D(T![]() )+(k-i)+D(T
)+(k-i)+D(T![]() )
)
Поэтому наименьшее значение D (Т) дается равенством
D(k)=![]() [k+D(i)+D(k-1)]. (3.1)
[k+D(i)+D(k-1)]. (3.1)
Учитывая предположение индукции, получаем отсюда
D(k)![]() k+
k+![]() [i log i+(k-i)log(k-i)] (3.2)
[i log i+(k-i)log(k-i)] (3.2)
Легко показать, что этот минимум достигается при i=k/2. Следовательно, D(k)![]() k+k log
k+k log ![]() =k log k
=k log k
Таким образом, D (m)![]() m log m для всех m
m log m для всех m![]() 1.
1.
Теперь мы утверждаем, что дерево решений Т, упорядочивающее n случайных элементов, имеет не меньше /г! листьев. Более того, в точности п\ листьев появляются с вероятностью 1/n! каждый, а остальные — с вероятностью 0. Не изменяя средней глубины дерева Т можно удалить из него все узлы, которые являются предками только листьев вероятности 0. Тогда останется дерево Т' с n! листьями, каждый из которых достигается с вероятностью 1/п!. Так как D(Т')![]() n! log n!, то средняя глубина дерева Т' (а значит, и Т) не меньше (1/n!) n! log n! = log n!.
n! log n!, то средняя глубина дерева Т' (а значит, и Т) не меньше (1/n!) n! log n! = log n!.
Следствие. Любая сортировка с помощью сравнений выполняет в среднем не менее сп log n сравнений для некоторой постоянной с>0.
Заслуживает упоминания эффективный алгоритм, называемый Быстрсорт, поскольку среднее время его работы, хотя и ограничено снизу функцией сn lоg n для некоторой постоянной с (как и у всякой сортировки с помощью сравнений), но составляет лишь часть времени работы других известных алгоритмов при их реализации на большинстве существующих машин. В худшем случае Быстрсорт имеет квадратичное время работы, но для многих приложений это не существенно.
Procedure БЫСТРСОРТ(S):
1. if S содержит не больше одного элемента then return S
else
begin выбрать произвольный элемент a из S;
2. пустьS1, S2 и S3 — последовательности элементов из S,
соответственно меньших, равных и больших а;
3. return (БЫСТРСОРТ(S1), затем S2, затем БЫСТРСОРТ (S3))
end
Рисунок 3.7. Программа Быстрсорт.
Алгоритм 3.5. Быстрсорт
Вход. Последовательность S из n элементов aь a2, ... , aп.
Выход. Элементы последовательности S, расположенные по порядку.
Метод. Рекурсивная процедура БЫСТРСОРТ определяется на рис. 3.7. Алгоритм состоит в вызове БЫСТРСОРТ(S).
Теорема 3.8. Алгоритм 3.5. упорядочивает последовательность из п элементов за среднее время О (п log п).
Доказательство. Корректность алгоритма 3.5 доказывается прямой индукцией по длине последовательности S. Чтобы проще было анализировать время работы, допустим, что все элементы в S различны. Это допущение максимизирует размеры последовательностей S1 и S3, которые строятся в строке 3, и тем самым максимизирует среднее время, затрачиваемое в рекурсивных вызовах в строке 4. Пусть Т (n) — среднее время, затрачиваемое алгоритмом БЫСТРСОРТ на упорядочение последовательности из n элементов. Ясно, что Т(0)=Т(1)=b для некоторой постоянной b.
Допустим, что элемент а, выбираемый в строке 2, является 1-м наименьшим элементом среди n элементов последовательности S. Тогда на два рекурсивных вызова БЫСТРСОРТ в строке 4 тратится среднее время Т(i - 1) и Т (n - i) соответственно. Так как i равновероятно принимает любое значение между 1 и n, а итоговое построение последовательности БЫСТРООРТ(S) очевидно занимает время cn для некоторой постоянной с, то
T(n)![]() cn+
cn+![]() [T(i-1)+T(n-1)] для n
[T(i-1)+T(n-1)] для n![]() 2
(3.3)
2
(3.3)
Алгебраические преобразования в (3.3) приводят к неравенству
T(n)![]() cn+
cn+![]()
![]() T(i) (3.4)
T(i) (3.4)
Покажем, что при n![]() 2 справедливо неравенство Т (n)<kn 1n n, где k=2с+2b и b=Т(0)=T(1). Для базиса (n=2) неравенство Т(2)
2 справедливо неравенство Т (n)<kn 1n n, где k=2с+2b и b=Т(0)=T(1). Для базиса (n=2) неравенство Т(2)![]() 2с+2b непосредственно вытекает из (3.4). Для проведения шага индукции запишем (3.4) в виде
2с+2b непосредственно вытекает из (3.4). Для проведения шага индукции запишем (3.4) в виде
T(n)![]() cn +
cn +![]() +
+ ![]()
![]() ki ln i (3.5)
ki ln i (3.5)
Так как функция i ln i вогнута, легко показать, что
![]() i ln i
i ln i ![]()
![]() x ln x dx
x ln x dx ![]()
![]() (3.6)
(3.6)
Подставляя (3.6) в (3.5), получаем
T(n)![]() cn +
cn + ![]() + kn ln n -
+ kn ln n - ![]()
Поскольку n![]() 2 и k=2с+2b, то сn+4 b/n
2 и k=2с+2b, то сn+4 b/n![]() kn/2. Таким образом, неравенство Т (n)
kn/2. Таким образом, неравенство Т (n)![]() kn 1n n следует из (3.7).
kn 1n n следует из (3.7).
Рассмотрим две детали, важные для практической реализации алгоритма. Первая — способ "произвольного" выбора элемента а в строке 2 процедуры БЫСТРСОРТ. При реализации этого оператора может возникнуть искушение встать на простой путь, а именно всегда выбирать, скажем, первый элемент последовательности S. Подобный выбор мог бы оказаться причиной значительно худшей работы алгоритма БЫСТРСОРТ, чем это вытекает из (3.3). Последовательность, к которой применяется подпрограмма сортировки, часто бывает уже "как-то" рассортирована, так что первый элемент мал с вероятностью выше средней. Читатель может проверить, что в крайнем случае, когда БЫСТРСОРТ начинает работу на уже упорядоченной последовательности без повторений, а в качестве элемента а всегда выбирается первый элемент из S, в последовательности S всегда будет на один элемент меньше, чем в той, из которой она строится. В этом случае БЫСТРСОРТ требует квадратичного числа шагов.
Лучшей техникой для выбора разбивающего элемента в строке 2 было бы использование генератора случайных чисел для порождения целого числа i, 1<i<|S| 1), и выбора затем i-го элемента из S в качестве а. Более простой подход — произвести выборку элементов из S, а затем взять ее медиану в качестве разбивающего элемента. Например, в качестве разбивающего элемента можно было бы взять медиану выборки, состоящей из первого, среднего и последнего элементов последовательности S.
Вторая деталь — как эффективно разбить S на три последовательности S1, S2 и S3? Можно (и желательно) иметь в массиве А все n исходных элементов. Так как процедура БЫСТРСОРТ вызывает себя рекурсивно, ее аргумент S всегда будет находиться в последовательных компонентах массива, скажем A[f], A[f+1], ..., A[l] для некоторых f и l, 1<f<n. Выбрав "произвольный" элемент а, можно устроить разбиение последовательности S на этом же месте. Иными словами, можно расположить S1 в компонентах A[f], A[f+1], ... A[k], а S2![]() S3— в A[k+1], A[k+2], ..., A[l] при некотором k, f
S3— в A[k+1], A[k+2], ..., A[l] при некотором k, f![]() k
k![]() lЗатем можно, если нужно, расщепить S2
lЗатем можно, если нужно, расщепить S2![]() S3, но обычно эффективнее просто рекурсивно вызвать БЫСТРСОРТ на S1 и S2
S3, но обычно эффективнее просто рекурсивно вызвать БЫСТРСОРТ на S1 и S2![]() S3, если оба этих множества не пусты.
S3, если оба этих множества не пусты.
По-видимому, самый легкий способ разбить S на том же месте — это использовать два указателя на массив, назовем их i и j. Вначале
1. begin
2. i![]() f;
f;
3. while i![]() j do
j do
begin
4. while A[i]>а и j>f do j![]() j - 1;
j - 1;
5. while A[j]<а и i![]() l do i
l do i![]() i + 1;
i + 1;
Похожие работы
... в виде небольших практических заданий, либо повторения изученного материала для написания тестов. Характер учебного материала. Учебный материал, используемый учителем при изучении такой темы как "Текстовый редактор Microsoft Word", носит комбинационный характер, так как включает в себя описательный, информационный, обобщающий и теоретический типы. Он преподает нам описание различных пунктов ...
... b) сервис c) вставка Тест для проверки знаний учащихся может быть также оформлен в виде программы. Краткий сценарий программы Тест: 1) На экран выводится название программы – Тест, и тема – Текстовый редактор Word. Внизу надпись: “Нажмите любую клавишу”. 2) Затем на экран выводится инструкция по работе с программой. 3) После этого запускается сам тест. На экране появляется вопрос и 3 ...
... одновременно открывать несколько файлов и быстро переключаться между ними, щелкая по ярлычкам. 5. Практическая часть работы Требовалось создать сайт с одноименным названием курсовой работы, а именно «Сравнительный анализ современных текстовых редакторов». Сайт создан с целью доведения информации о текстовых редакторах до всех желающих. Структура папок для хранения структуры сайта ...
... этой процедуры необходимо иметь: главный документ, содержащий постоянную информацию; документ-источник для хранения переменной информации. 4. Интерфейс текстового редактора MS Word MS WORD - это эффективный и полнофункциональный текстовый редактор, который предоставляет все средства, необходимые для создания документов различных типов. Интерфейс Microsoft Word Полосы прокрутки ...

0 комментариев